集成学习是将多个基学习器(模型)相结合来完成学习任务。
随机森林:
随机森林是一种常见的集成学习方式。
前面我们学习了决策树,决策树生成后,我们可以利用同样的方法对训练集构建多棵决策树;
构建多棵决策树使用了数据样本随机和属性随机。
- 构建多棵决策树的过程中,对于构建一棵决策树我们可以规定每次随机取训练集的n%个数据,这样可以减少异常值点对构建随机森林造成的影响;
- 在选择属性(特征)时也随机选择多个构建一棵决策树。(样本随机性,特征(属性)随机性),即在当前节点选择一个属性子集来选择最优属性,通常一个属性子集选择个属性,而不是将所有的属性计算熵来选择最优属性构造节点。
对于回归问题,测试集可以取这些决策树结果的均值,即平均法,分类问题,测试结果可以取其中分类概率最大的类别(分类结果最多,若相同,则可随机选择一个),即投票法。
Bagging
Bootstrping:有放回采样,即一个盒子里面有10个白球,每次取三个球后将球放回,下次取还是这十个球。
Bagging:有放回n个样本一起建立分类器
Bagging和随机森林都是并行式集成学习的代表,即各个基学习器之间的训练没有关系,可同时训练,Bagging使用的是自助采样法(即有放回的取部分样本进行基学习器的训练),假设取样得到T组样本,每组m个,我们可以单独使用每组样本进行学习器的训练,可以得到T个基学习器,然后将这些学习器进行组合就是Bagging的基本思想。
Bagging通常也可以采用简单平均法和投票法决定最终的结果。
基本过程如下:
其中是自助采样产生的样本分布,表示样本的真实标记集合。即选择使得预测正确最高的结果。
Bagging还有一个特性,在自助采样的过程中,有可能有的样本被多次选取,但有些样本可能一次都未被选取,因此我们可以在采样过程中将样本进行标记,训练结束后,可以使用这些未被选取训练的样本做为验证集,来测试模型的好坏。
Bagging注重关注降低方差,它在不剪枝决策树、神经网络等容易受样本扰动的学习器上效果更明显。下面是基于Bagging的决策树的不同规模的集成和分类边界的结果。
Boosting
和前面随机森林和Bagging的并行式学习不一样,Boost是串行式的学习,即每一步的学习器由前一步的学习器迭代产生。
大致算法:先从训练集中训练出一个基学习器,根据基学习器的表现对样本的分布进行调整,增加识别错误的样本的权重,使这些样本更加被重视,经过样本分布的调整后来训练下一个基学习器,重复进行,达到事先预定的T轮后停止,然后将这T个学习器进行加权结合。
一次更新的结果如下:
是每次更新的权重,在第一次时将每个样本的权重初始化,经过一次学习调高错误样本的权值,降低正确样本的权值,与一般学习器的损失函数相比它的损失函数只是加上了权值。表示第n个样本的预测值,表示第n个样本的实际值。那么权重的变化应该遵循怎样的规律呢,常见的有Adaboost来更新权重。
Adaboost
(原始的Adaboost算法只适用于二分类问题。)
Adaboost常见的形式:
是基学习器的线性组合。
举例:表示权重,表示样本。表示实际标记。下标表示某次迭代(第几个基学习器)
更新权重:
- 如果第一次的样本分类错误,即,我们更新样本的权重;提升样本的权重,使得分类错误的样本更容易被重视。
- 如果分类正确,则,即降低样本的权重。
调整权重的推导过程:
对于错误率是第一个基学习器产生的结果,我们希望通过调整错误样本的权重使得此时的(大于0.5时,学习器还不如随机过程,没有意义),使得错误样本在下一次的训练中得到重视,然后进行下一个学习器的训练,因此有下面的过程:
经过上面的代换可得到:
将分子分母颠倒:
所以:
即:
因为,所以上式可代换:
所以:
举例:
第一次迭代:
改变样本权重,进行第二次迭代:
重复上面的过程:
经过三轮后,将上面的三个学习器进行加权结合,产生分类结果:
其中: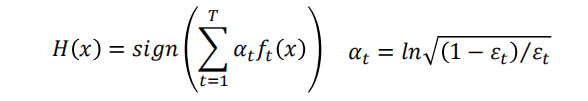
Boosting主要注重降低偏差,因此Boosting能基于泛化性能相当弱(容易过拟合)的学习器构建强的集成。
在集成各个基学习器的过程中,一般而言,在个体学习器性能相差较大时宜使用加权平均法结合基学习器,在个体学习器性能相近时,使用简单平均法。
来源:https://blog.csdn.net/qq_35649945/article/details/99169453