20182301 2019-2020-1 《数据结构与面向对象程序设计》实验9报告
课程:《程序设计与数据结构》
班级: 1823
姓名: 赵沛凝
学号:20182301
实验教师:王志强
实验日期:2019年12月2日
必修/选修: 必修
1.实验内容
- 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
- 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
- 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
- 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
- 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
2. 实验过程及结果
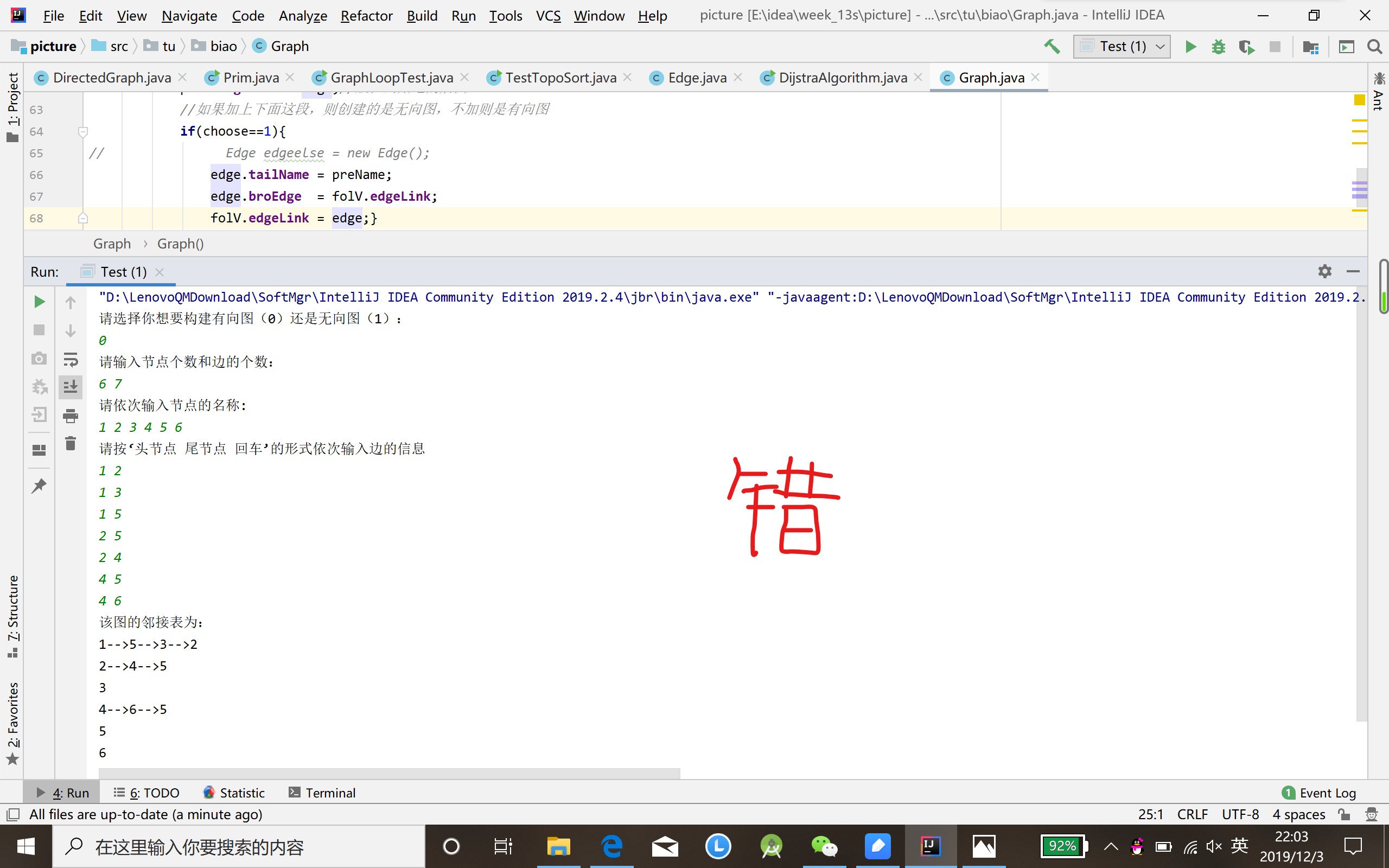
初始化无向图和有向图:
- 有向图的建立算法
System.out.println("请按‘头节点 尾节点 回车’的形式依次输入边的信息");
for (int i=0;i<edgeNum;i++){
String preName = scan.next();
String folName = scan.next();
Vertex preV = getVertex(preName);
Vertex folV = getVertex(folName);
if (preV == null || folV == null){ System.out.println("输入错误,输入了不存在的顶点!请重新输入");
i--;
continue;
}
Edge edge = new Edge();
edge.tailName = folName;
//将边加入到节点的链表中去
edge.broEdge = preV.edgeLink;//循环
preV.edgeLink = edge;//放在出始地的后面

- 无向图的建立很巧妙的再加一段就可以,如下:
Edge edgeelse = new Edge();
edgeelse.tailName = preName;
edgeelse.broEdge = folV.edgeLink;
folV.edgeLink = edgeelse;
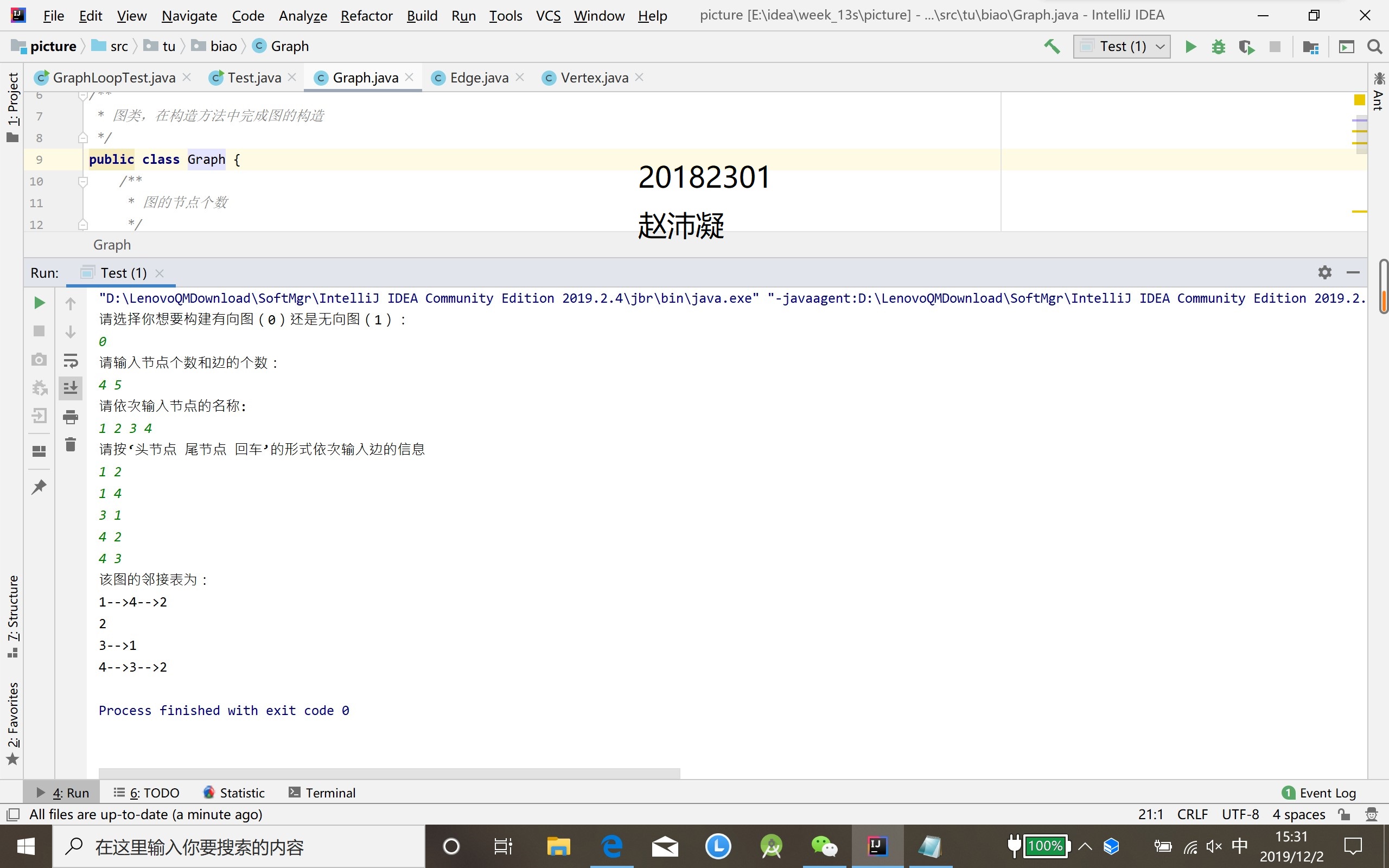
有向图和无向图的遍历
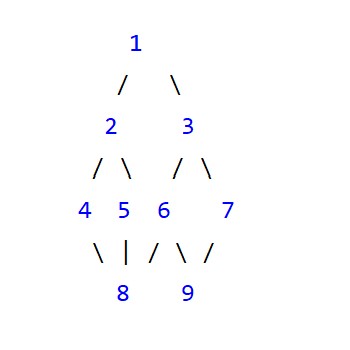
- BFS使用队列(queue)来实施算法过程
private Queue<String> queue = new LinkedList<String>();
private Map<String, Boolean> status = new HashMap<String, Boolean>();
public void BFSSearch(String startPoint) {
//1.把起始点放入queue;
queue.add(startPoint);
status.put(startPoint, false);
bfsLoop();
}
private void bfsLoop() {
// 1) 从queue中取出队列头的点;更新状态为已经遍历。
String currentQueueHeader = queue.poll(); //出队
status.put(currentQueueHeader, true);
System.out.println(currentQueueHeader);
// 2) 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中。
List<String> neighborPoints = graph.get(currentQueueHeader);
for (String poinit : neighborPoints) {
if (!status.getOrDefault(poinit, false)) { //未被遍历
if (queue.contains(poinit)) continue;
queue.add(poinit);
status.put(poinit, false);
}
}
if (!queue.isEmpty()) { //如果队列不为空继续遍历
bfsLoop();
}
}
- DFS使用队列(queue)来实施算法过程
private Stack<String> stack = new Stack<String>();
public void DFSSearch(String startPoint) {
stack.push(startPoint);
status.put(startPoint, true);
dfsLoop();
}
private void dfsLoop() {
if(stack.empty()){
return;
}
//查看栈顶元素,但并不出栈
String stackTopPoint = stack.peek();
// 2) 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中。
List<String> neighborPoints = graph.get(stackTopPoint);
for (String point : neighborPoints) {
if (!status.getOrDefault(point, false)) { //未被遍历
stack.push(point);
status.put(point, true);
dfsLoop();
}
}
String popPoint = stack.pop();
System.out.println(popPoint);
}
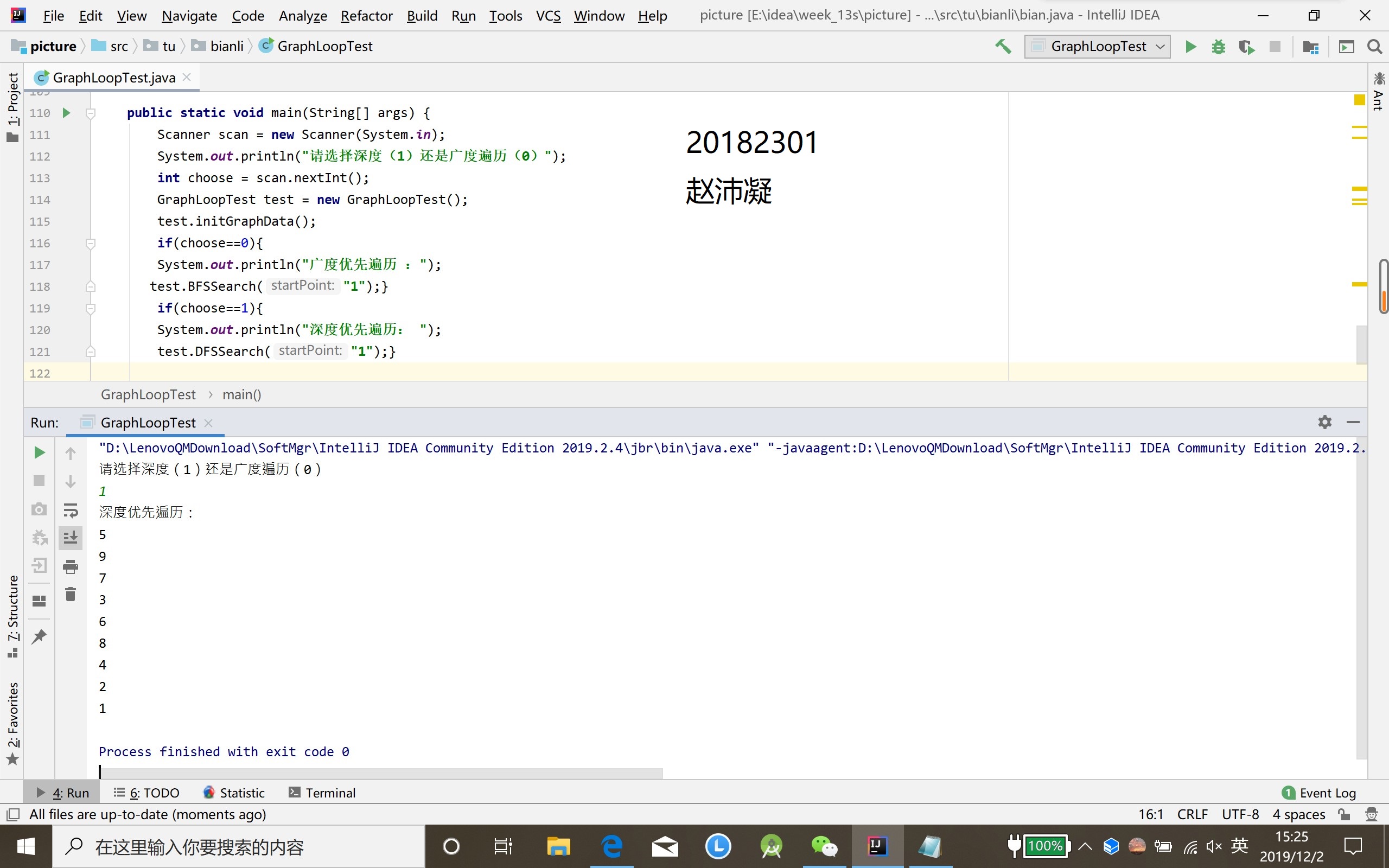
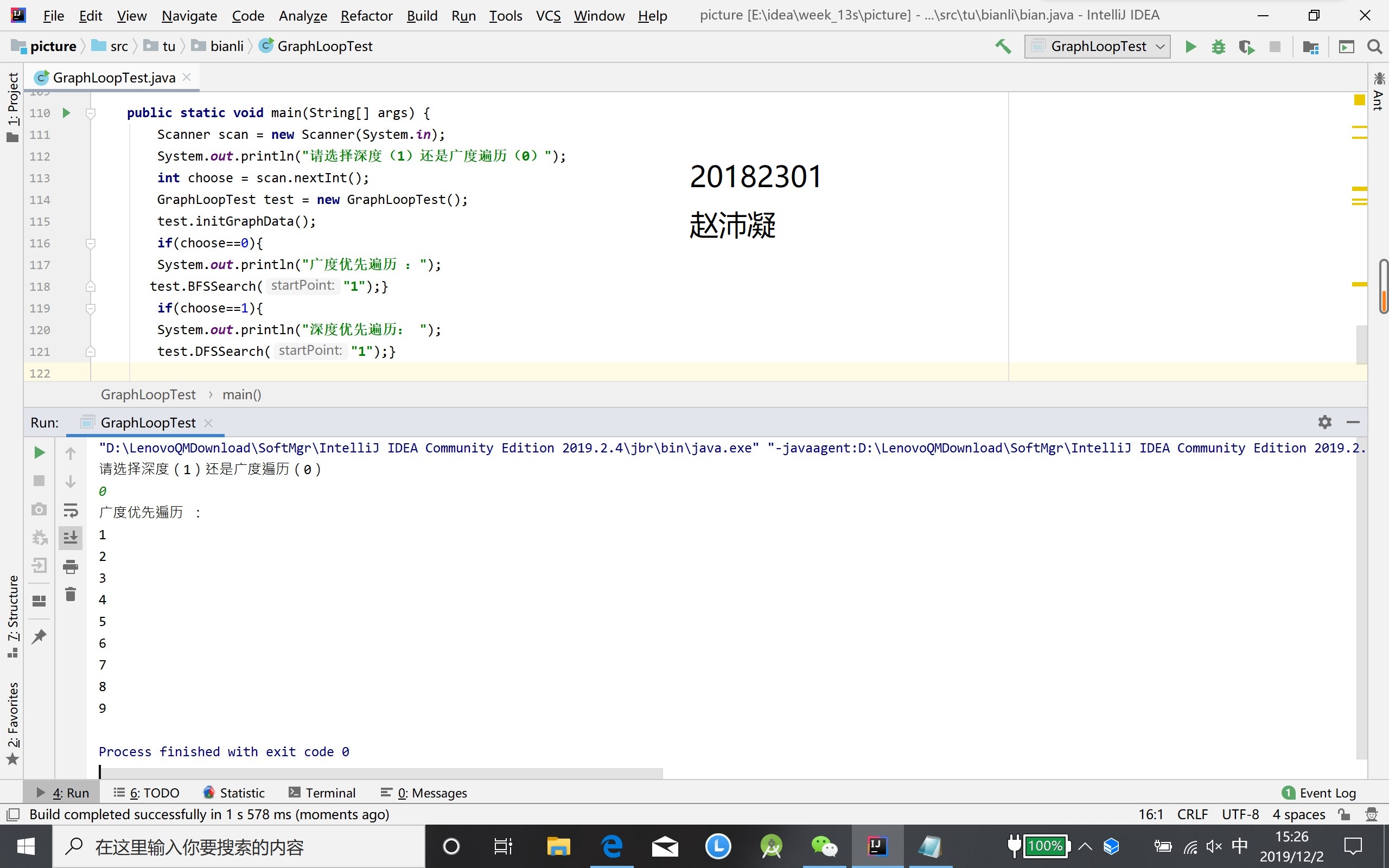
有向图的拓扑排序
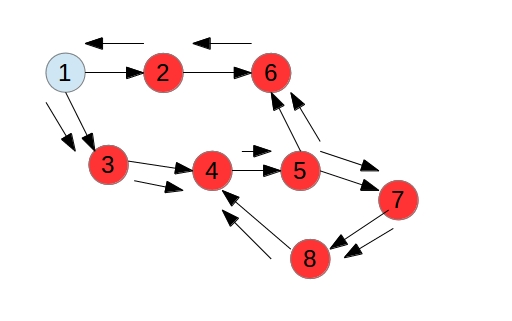
- 先初始化
startNode = directedGraph.get(startNodeLabel);
if (startNode == null) {
startNode = new Vertex(startNodeLabel);
directedGraph.put(startNodeLabel, startNode);
}
endNode = directedGraph.get(endNodeLabel);
if (endNode == null) {
endNode = new Vertex(endNodeLabel);
directedGraph.put(endNodeLabel, endNode);
}
e = new Edge(endNode);//每读入一行代表一条边
startNode.adjEdges.add(e);//每读入一行数据,起始顶点添加一条边
endNode.inDegree++;//每读入一行数据,终止顶点入度加1
- 判断圆环
Queue<Vertex> queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
//扫描所有的顶点,将入度为0的顶点入队列
Collection<Vertex> vertexs = directedGraph.values();
for (Vertex vertex : vertexs)
if(vertex.inDegree == 0)
queue.offer(vertex);
while(!queue.isEmpty()){
Vertex v = queue.poll();
System.out.print(v.vertexLabel + " ");
count++;
for (Edge e : v.adjEdges)
if(--e.endVertex.inDegree == 0)
queue.offer(e.endVertex);
}
if(count != directedGraph.size()){
throw new Exception("Graph has circle");
}
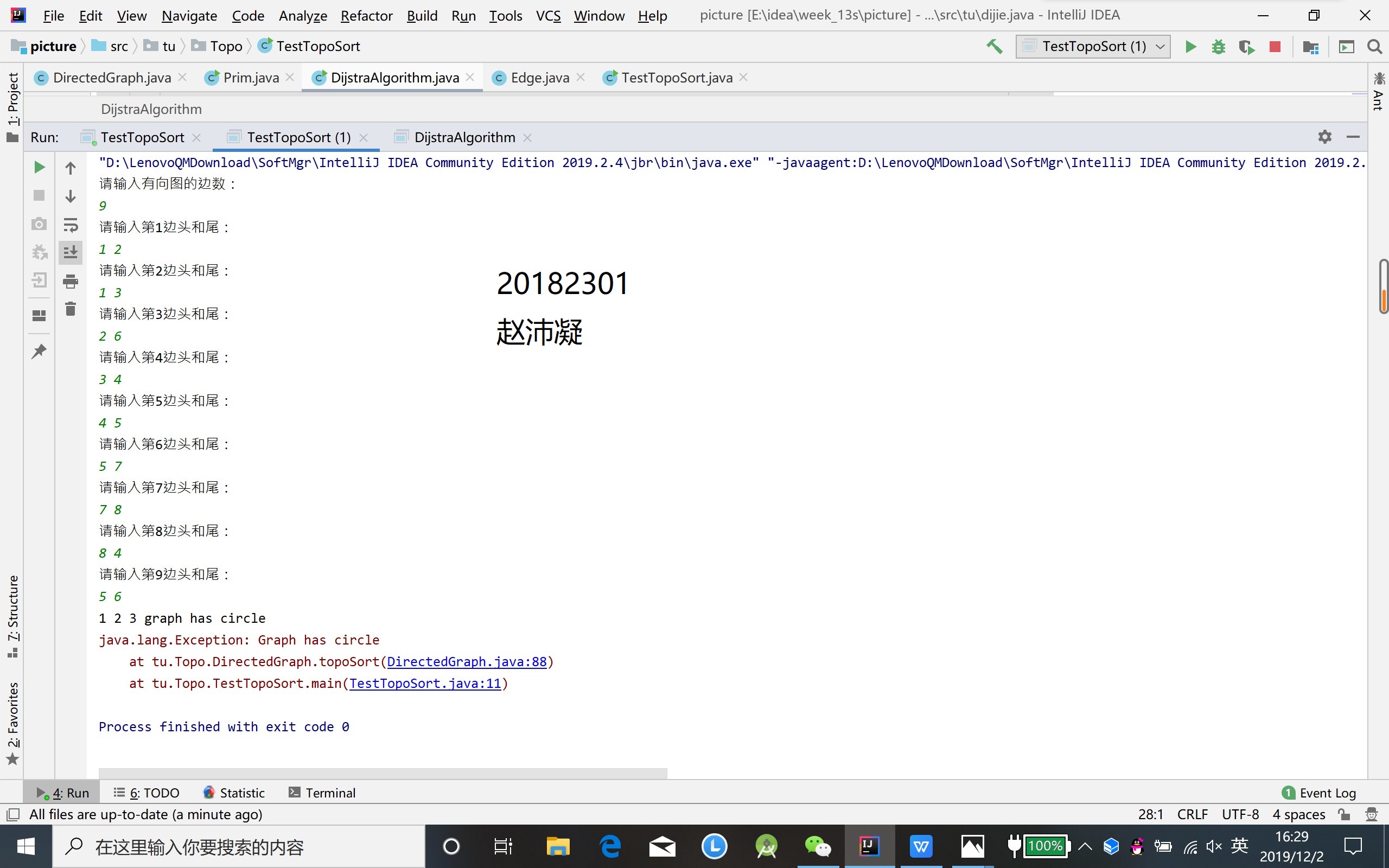
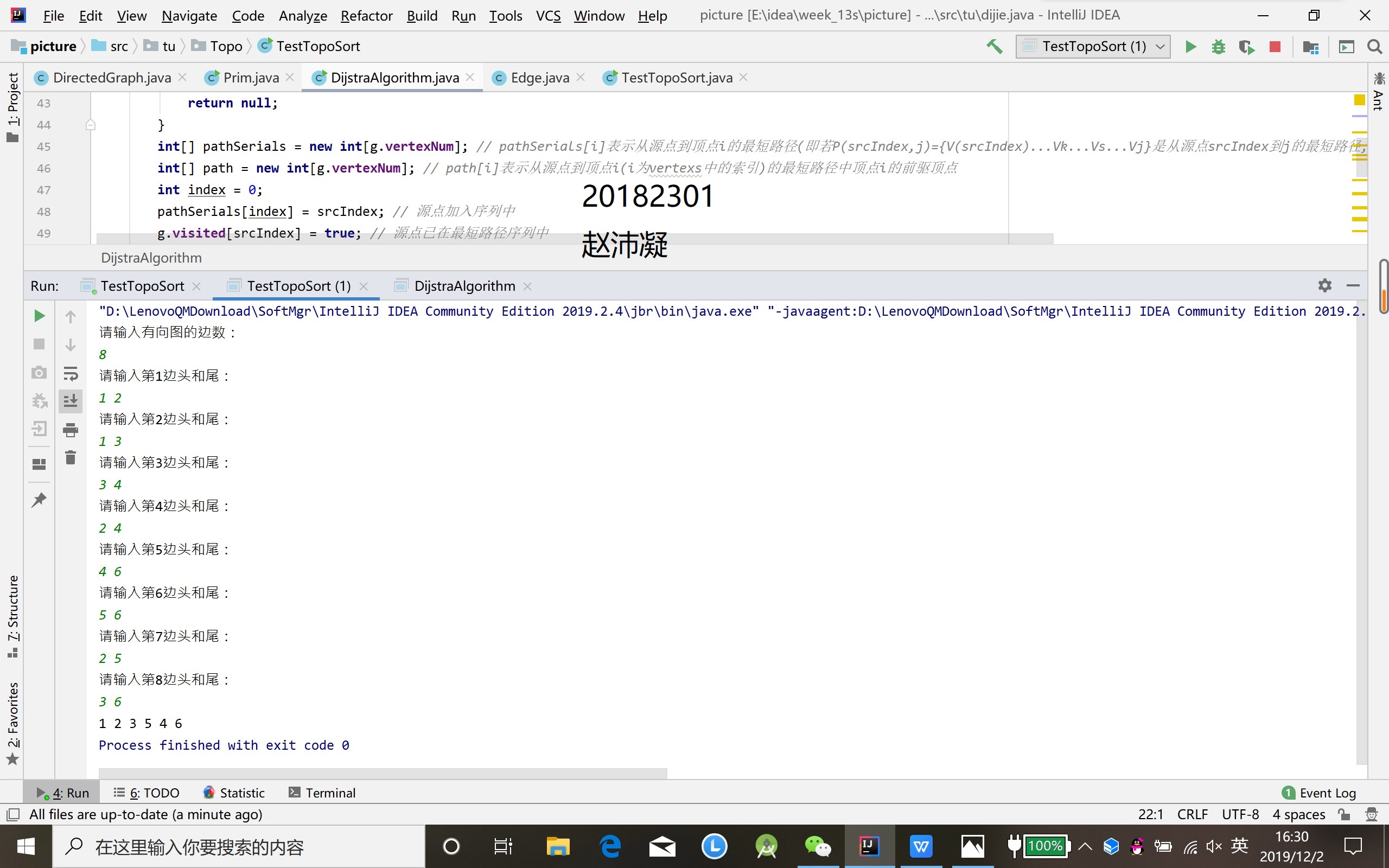
无向图的最小生成树

- 建立边并进行对比
public Edge(int i,int j,int w){
this.i=i;
this.j=j;
this.w=w;
}
@Override
public int compareTo(Object o) {
Edge to=(Edge)o;
if(this.w>to.w) return 1;
else if(this.w==to.w) return 0;
else return -1;
}
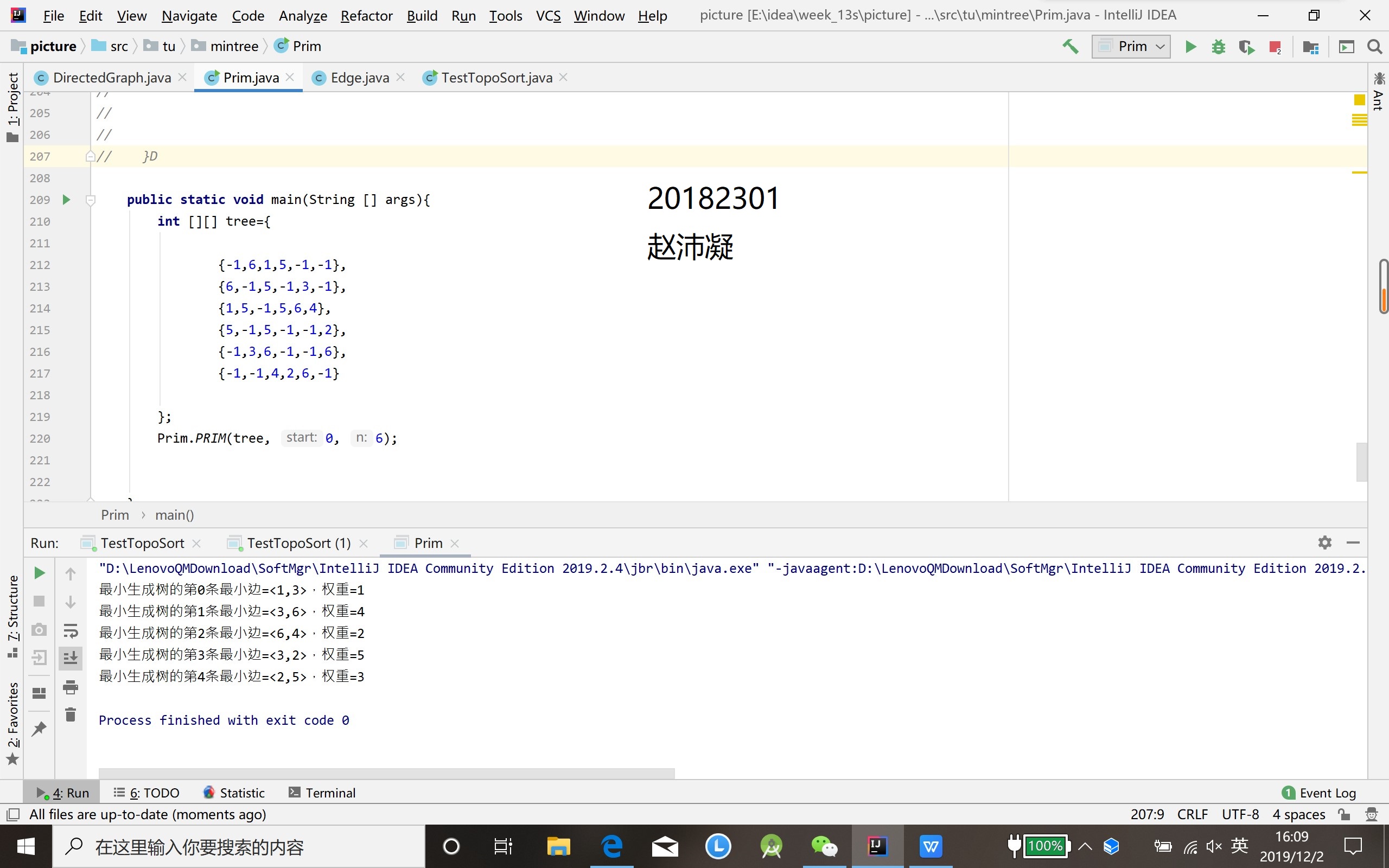
单源最短路径求解

- 通过迪杰斯特拉(Dijkstra)算法求以vertex[srcIndex]顶点作为源点到其余各顶点的最短路径
public static Info dijkstra(Graph g, int srcIndex) {
if(srcIndex < 0 || srcIndex >= g.vertexNum){
return null;
}
int[] pathSerials = new int[g.vertexNum]; // pathSerials[i]表示从源点到顶点i的最短路径(即若P(srcIndex,j)={V(srcIndex)...Vk...Vs...Vj}是从源点srcIndex到j的最短路径,则有P(srcIndex,j)=P(srcIndex,k)+P(k,s)+P(s,j))
int[] path = new int[g.vertexNum]; // path[i]表示从源点到顶点i(i为vertexs中的索引)的最短路径中顶点i的前驱顶点
int index = 0;
pathSerials[index] = srcIndex; // 源点加入序列中
g.visited[srcIndex] = true; // 源点已在最短路径序列中
Arrays.fill(path, -1); // -1表示顶点没有前驱顶点
int[] distances = new int[g.vertexNum]; // distances[i]表示从源点到顶点i(i为vertexs中的索引)的当前最短路径长度
for (int i = 0; i < g.vertexNum; i++) {
// 初始化distances为其余顶点到源点的权值
distances[i] = g.matrix[srcIndex][i];
}
int minIndex = srcIndex;
while (minIndex != -1) { // 仍有未加入到最短路径序列中的顶点
index++;
for (int i = 0; i < g.vertexNum; i++) {
if (!g.visited[i]) { // 更新仍未加入到最短路径序列中的顶点的从源点到它的值
// 这些仍未加入到最短路径序列中的顶点的distances[i]值为(刚加入的顶点minIndex的distances[minIndex]与minIndex到顶点i之和)与(顶点minIndex刚加入之前源点到i的距离值distances[i])两者之间的较小者
distances[i] = Math.min(distances[i], distances[minIndex] + g.matrix[minIndex][i]);
// 如果当前顶点i的distances[i]值为新加入的顶点minIndex,则顶点i的前驱为minIndex,否则不变
if(distances[i] == distances[minIndex] + g.matrix[minIndex][i] && distances[i] != Integer.MAX_VALUE / 2){ // distances[i] != Integer.MAX_VALUE / 2表示仍不可达,就没有前驱
path[i] = minIndex;
}
}
}
minIndex = indexOf(g, distances); // 选出的最小顶点
if(minIndex == -1){
break;
}
pathSerials[index] = minIndex; // 刚选出的最小顶点加入到最短路径序列中
g.visited[minIndex] = true;
}
return new Info(distances, pathSerials, getPathOfAll(path, pathSerials));
}
- 找到图中仍未加入到最短路径序列顶点集中到源点距离最小的顶点的索引
public static int indexOf(Graph g, int[] distances) {
int min = Integer.MAX_VALUE / 3;
int minIndex = -1; // 当前数组distances剩余元素最小值(-1表示无剩余元素)--剩余元素就是仍未加入到最短路径序列中的顶点
for(int i = 0; i < g.vertexNum; i++){
if(!g.visited[i]){ // 如果i顶点仍未加入到最短路径序列中
if(distances[i] < min){
min = distances[i];
minIndex = i;
}
}
}
return minIndex;
}
- 得到指定顶点i的从源点到顶点i的最短路径(均以顶点集vertexs中索引表示)
public static int[] getPath(int[] path, int i){
Stack<Integer> s = new Stack<Integer>();
s.push(i);
int pre = path[i];
while(pre != -1){
s.push(pre);
pre = path[pre];
}
int size = s.size();
int[] pathOfVertex = new int[size];
while(!s.isEmpty()){
pathOfVertex[size - s.size()] = s.pop();
}
return pathOfVertex;
}
- 最短路径
public static class Info{
private int[] distances; // 源点到各个顶点的最短距离
private int[] pathSerials; // 整个最短路径序列
private ArrayList<int[]> paths; // 源点到各个顶点的确切最短路径序列
public Info(int[] distances, int[] pathSerials, ArrayList<int[]> paths) {
this.distances = distances;
this.pathSerials = pathSerials;
this.paths = paths;
}
}
3. 实验过程中遇到的问题和解决过程
问题1:在第一题中,无向图的邻接链表总是出错,为什么?

- 问题1解决方案:
- 原本的代码
edge.tailName = preName; edge.broEdge = folV.edgeLink; folV.edgeLink = edge;
- 修改代码,建立新边
Edge edgeelse = new Edge(); edgeelse.tailName = preName; edgeelse.broEdge = folV.edgeLink; folV.edgeLink = edgeelse;
- 问题2:关于第五个,有向图的单源最短路径求解(迪杰斯特拉算法),一开始并不是很明白,于是搜索博客加深理解。
- 问题2解决方案:
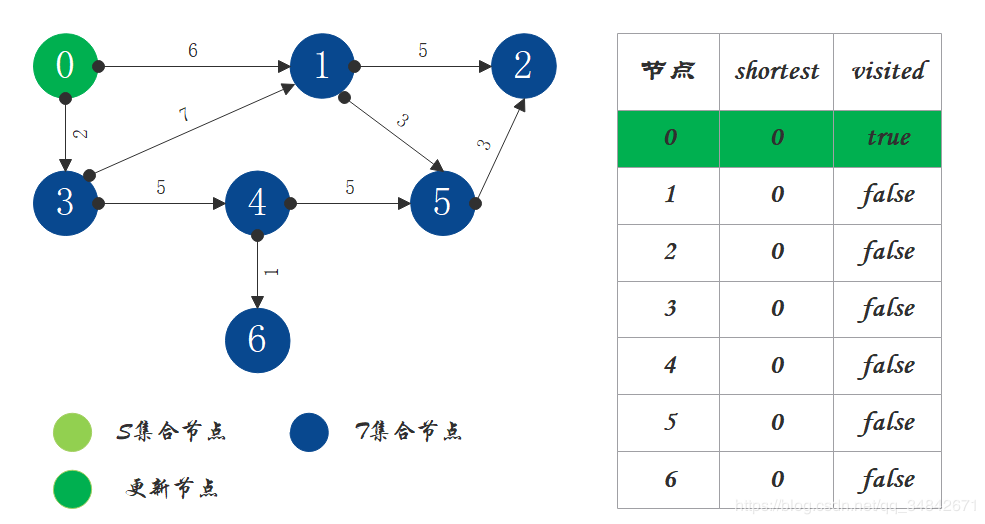
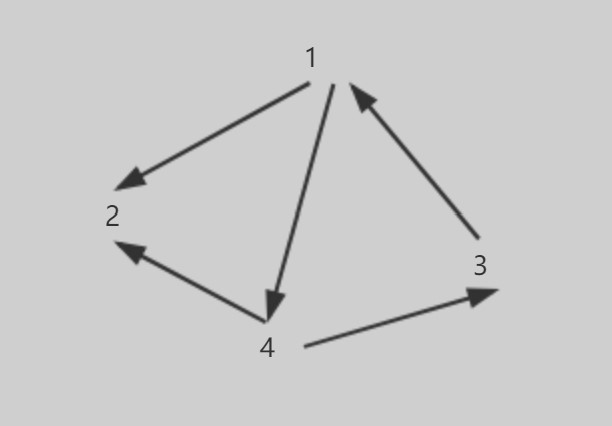
将源节点(即节点0)加入S中,对shortest和visited数组进行更新。

S中现有节点0,源节点可达T中的节点1和节点3,节点0->节点1距离为6,节点0->节点3距离为2,按距离从小到大排序,因此选择将节点3加入S中。更新源点将节点3作为中间节点到达其它节点的距离。

S中现有节点0和节点3,源节点可达T中的节点1和4,节点0->节点1距离为6,节点0->节点4距离为7,按距离从小到大排序,因此选择将节点1加入S中。更新源点将节点1作为中间节点到达其它节点的距离。

S中现有节点0、1、3,源节点可达T中的节点2、4、5,0->2距离为11,0->4距离为7,0->5距离为9,按距离从小到大排序,因此选择将节点4加入S中。更新源点将节点4作为中间节点到达其它节点的距离。

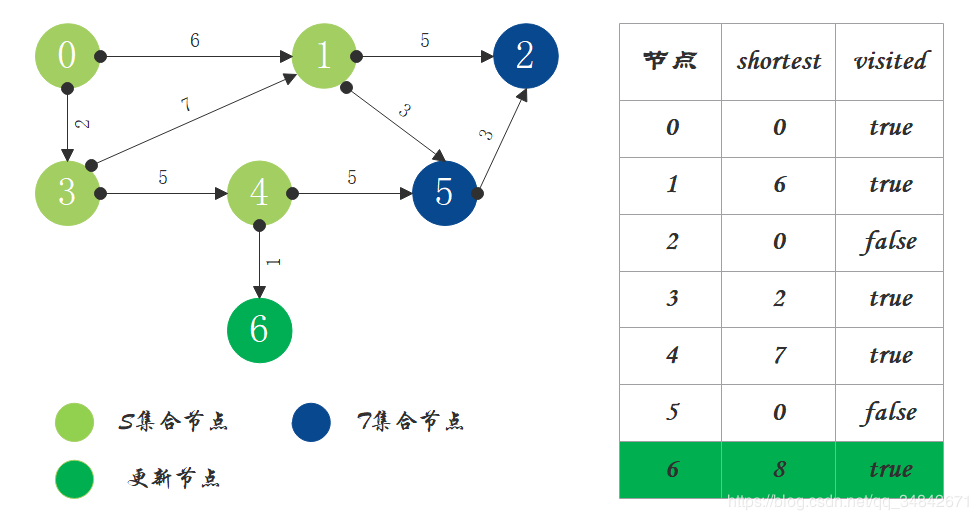
S中现有节点0、1、3、4,源节点可达T中的节点2、5、6,0->2距离为11,0->5距离为9,0->6距离为8,按距离从小到大排序,因此选择将节点6加入S中。更新源点将节点6作为中间节点到达其它节点的距离。

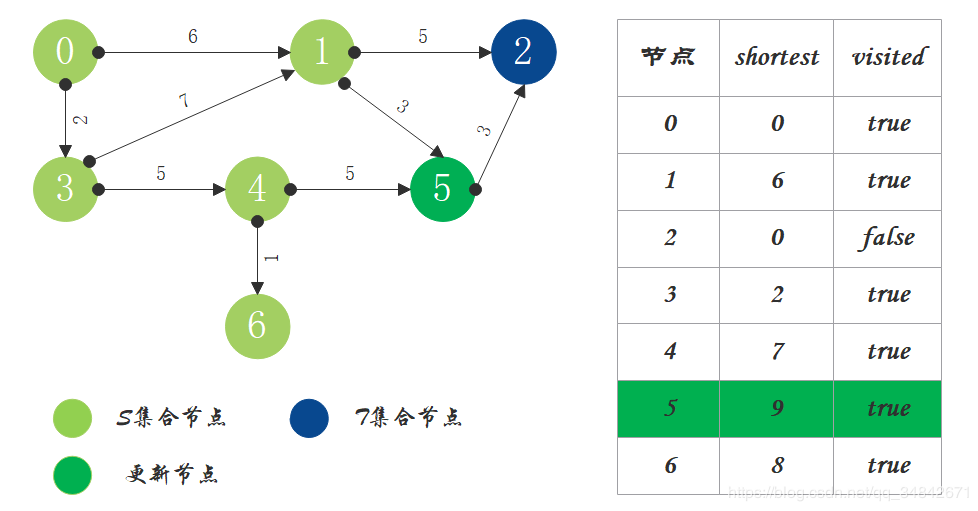
S中现有节点0、1、3、4、6,源节点可达T中的节点2、5,0->2距离为11,0->5距离为9,按距离从小到大排序,因此选择将节点5加入S中。更新源点将节点5作为中间节点到达其它节点的距离。

T中只剩下节点2,0->2距离为11,将节点2加入S中。
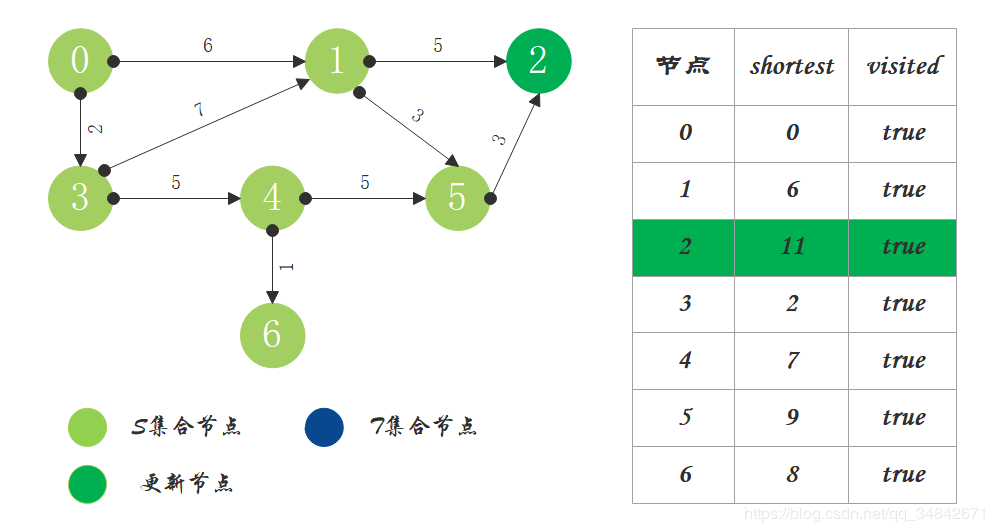
- 算法结束,源点到其它节点的最短路径都已依次求出。

其他(感悟、思考等)
如果每次都把老师讲的进行实践,那么实验也不会很费力。以后在学习过程中,也要循序渐进。