文章目录
Contest100000583 - 《算法笔记》4.3小节——算法初步->递归
4.3 递归
4.3.1 分治

4.3.2 递归

递归求解n的阶乘
//递归求解n的阶乘
#include <cstdio>
int F(int n)
{
if(n==0)
return 1;//递归边界
else
return F(n-1)*n;//递归表达式
}
int main()
{
int n;
scanf("%d",&n);
printf("%d\n",F(n));
return 0;
}
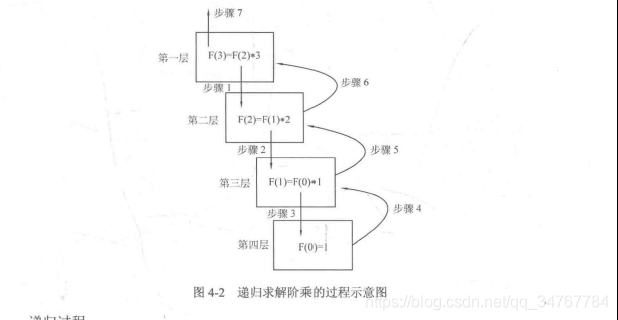
递归过程如图
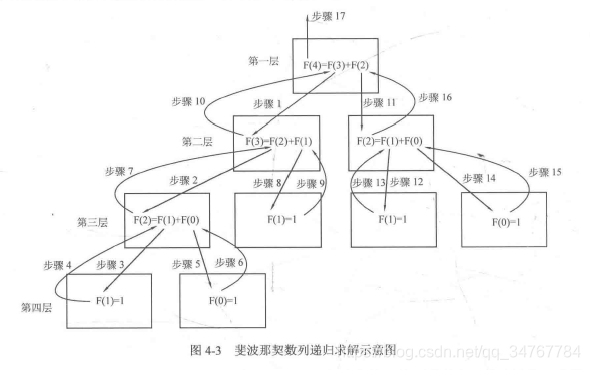
求斐波那契(Fibonacci)数列的第n项
//求斐波那契(Fibonacci)数列的第n项
#include <iostream>
#include <cstdio>
int F(int n)
{
if(n==0||n==1)
return 1;//递归边界
else
return F(n-1)+F(n-2);//递归式
}
int main()
{
int n;
scanf("%d",&n);
printf("%d\n",F(n));
return 0;
}
全排列

//感觉理解不透,还需琢磨
//全排列,n=3时
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 11;
//P为当前排列,hashTable记录整数x是否已经在P中
int n,P[maxn] = {false};
//当前处理排列的第index号位
void generateP(int index)
{
if(index == n+1)//递归边界,已经处理完排列的1~n位
{
for(int i=1;i<=n;i++)
{
printf("%d",P[i]);//输出当前排列
}
printf("\n");
return;
}
for(int x=1;x<=n;x++)//枚举1~n,试图将x填入P[index]
{
if(hashTable[x] == false)//如果x不在P[0]~P[index-1]中
{
P[index] = x;//令P的第index位为x,即把x加入当前排列
hashTable[x] = true;//记x已在P中
generateP(index+1);//处理排列的第index+1号位
hashTable[x] = false;//已处理完P[index]为x的子问题,还原状态
}
}
}
int main()
{
n=3;//欲输出1~3的全排列额
generateP(1);//从P[1]开始填
return 0;
}
n皇后问题
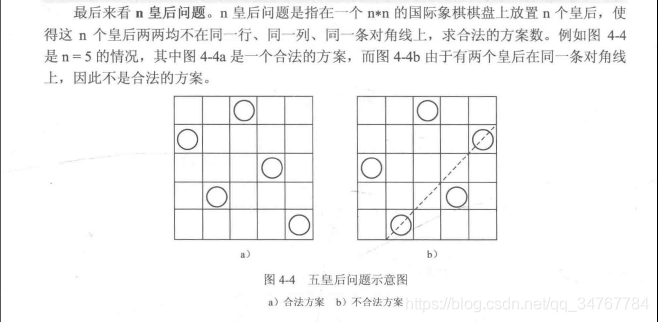
//n皇后问题暴力法
//基本思想:全组合考虑去除同行同列的情况,转化为全排列,然后判断合法性,暴力法
//主要代码如下:
int count = 0;
void generateP(int index)
{
if(index == n+1)//递归边界,生成一个排列
{
bool flag = true;//flag为true表示当前排列为一个合法方案
for(int i=1;i<=n;i++)//任意遍历两个皇后
for(int j=i+1;j<=n;j++)
{
if(abs(i-j) == abs(P[i]-P[j]))//如果在一条对角线上
{
flag = false;//不合法
}
}
}
if(flag)
count++;//若当前方案合法,令count加1
return;
}
for(int x=1;x<=n;x++)
{
if(hashTable[x] == false)
{
P[index] = x;
hashTable[x] = true;
generateP(index+1);
hashTable[x] = false;
}
}
//n皇后问题回溯法
void generateP(int index)
{
if(index == n+1)//递归边界,生成一个合法方案
{
count++;//能到达这里的一定是合法的
return;
}
for(int x=1;x<=n;x++)//第x行
{
if(hashTable[x] == false)//第x行还没有皇后
{
bool flag = true;//flag为true表示当前皇后不会和之前的皇后冲突
for(int pre = 1;pre<index;pre++)//遍历之前的皇后
{//第index列皇后的行号为x,第pre列皇后的行号为P[pre]
if(abs(index - pre) == abs(x - P[pre]))
{
flag = false;//与之前的皇后在一条对角线,冲突
break;
}
}
if(flag)//如果可以把皇后放在第x行
{
P[index] = x;//令第index列皇后的行号为x
hashTable[x] = true;//第x行已被占用
generateP(index + 1);//递归处理第index+1行皇后
hashTable[x] = false;//递归完毕,还原第x行为未占用
}
}
}
}
练习
Contest100000583 - 《算法笔记》4.3小节——算法初步->递归
来自 http://codeup.cn/contest.php?cid=100000583
1907 Problem A 吃糖果
来自 http://codeup.cn/contest.php?cid=100000583
题析:简单递归应用
//1907ProblemA 吃糖果
#include <iostream>
#include <cstdio>
using namespace std;
int candy_method(int n)
{
if(n==1)//递归边界条件
return 1;
else if(n==2)
return 2;
else//递归式
return candy_method(n-1)+candy_method(n-2);
}
int main()
{
int n;
while(scanf("%d",&n) != EOF)
{
printf("%d\n",candy_method(n));
}
return 0;
}
2018 Problem B 数列
来自 http://codeup.cn/contest.php?cid=100000583
//2018ProblemB数列
#include <iostream>
#include <cstdio>
using namespace std;
int Fib(int n)//斐波那契数列
{
if(n==0)//递归边界条件
return 0;
if(n==1)
return 1;
else//递归式
return Fib(n-1)+Fib(n-2);
}
int main()
{
int m;
scanf("%d",&m);
while(m--)
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
for(int j=0;j<2*(n-i-1);j++)//注意2倍,注意n-(i+1),i从0开始
printf(" ");
for(int k=0;k<2*i+1;k++)//1/3/5/7'''2*n+1
{
printf("%d ",Fib(k));
}
printf("\n");
}
}
return 0;
}
2044 Problem C 神奇的口袋
来自 http://codeup.cn/contest.php?cid=100000583
题析:
膜大佬:一题多解
https://blog.csdn.net/qq_36502291/article/details/82859837
这个思路较清晰:
https://blog.csdn.net/ActionBeam/article/details/88385533
总结一下,递归问题主要就是两块,递归边界条件(可以不止一个),递归表达式
这里从实际问题的数学模型就是,从n个数中选择若干数使得其和为40,问共有多少种选择方法。
我们用数组arr[]记录所给的数字,下标为从1~n,然后从最后成功或失败的结果倒推
边界条件:
1)特殊情况sum等于0,则默认为1种
2)若逆着追溯到 i等于0,则说明i等于1时仍不能满足题意,所以不存在方案满足题意
剩下的就是常规的递归表达式:
i) 可能为不选择最后一个数arr[i],转化为从i-1个数中选择若干个数和为sum
ii)可能为选择最后一个数,转化为下一层递归,即从i-1个数中选择若干数和为sum-arr[i]
//2044ProblemC神奇的口袋
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 25;
int arr[MAXN];
int select(int sum,int i)//从前i个数中选择数和为sum
{
//边界条件
if(sum==0)//和为0,啥都不用取
return 1;
if(i==0)//i为0表示已经没有数了,没有找到符合条件的
return 0;
//递归表达式
return select(sum-arr[i],i-1)+select(sum,i-1);
//select(sum-arr[i],i-1)
//表示取最后一个数arr[i],转换为取钱i-1个数,和为sum-arr[i]
//select(sum,i-1)表示不取最后一个数arr[i],
}
int main()
{
int n;
while(scanf("%d",&n) != EOF)
{
for(int i=1;i<=n;i++)//读入数组数据
{
scanf("%d",&arr[i]);
}
int result = select(40,n);
printf("%d\n",result);
}
return 0;
}
2046 Problem D 八皇后
来自 http://codeup.cn/contest.php?cid=100000583
题析:经典八皇后问题
//2046ProblemD八皇后
//参考前面讲解里面的八皇后回溯法
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=105;
int N,cnt=0,P[maxn];
char result[105][15]={0};
bool hashTable[maxn] = {false};
void generateP(int index)
{
//递归边界
if(index == N+1)//若是排列的n位已经处理完,则递归结束
{
cnt++;
for(int i=1;i<=N;i++)//存储结果,形式为字符串
{
result[cnt][i-1] = P[i]+'0'; //形式为字符串
}
return;
}
//递归表达式
for(int x=1;x<=N;x++)//枚举1~n,试图将x填入P[index]
{
if(hashTable[x] == false)//如果x不在P[0]~P[index-1]中,第x行还没有皇后
{
bool flag=true;//flag为true表示当前皇后不会和之前的皇后冲突
for(int pre=1;pre<index;pre++)//遍历之前的皇后
{//第index列皇后的行号为x,第pre列皇后的行号为P[pre]
if(abs(index-pre) == abs(x-P[pre]))//此处的判别条件??
{
flag = false;//与之前的皇后在一条对角线,冲突
break;
}
}
if(flag)//如果可以把皇后放在第x行
{
P[index] = x;//令P的第index位为x,即把x加入当前排列
hashTable[x] = true;//记录x已在P中
generateP(index+1); //递归表达式,递归处理下一位
hashTable[x] = false;//当递归返回时已处理完P[index]的子问题,还原状态
}
}
}
}
int main()
{
N=8;
generateP(1);//预先处理
int n;
while(scanf("%d",&n) != EOF)//多点测试
{
while(n--)//n个数据
{
int m;
scanf("%d",&m);
printf("%s\n",result[m]);//输出第m个八皇后排列
}
}
return 0;
}
总结下:
递归最重要两点:
1)递归边界条件,跳出递归的地方
2)递归表达式,递归迭代的数学抽象
另外经典的递归:全排列、8皇后需记住
来源:CSDN
作者:qq_34767784
链接:https://blog.csdn.net/qq_34767784/article/details/89212995