一、顺序查找

线性查找是在一个已知无（或有序）序队列中找出与给定关键字相同的数的具体位置。原理是

让关键字与队列中的数从最后一个开始逐个比较，直到找出与给定关键字相同的数为止，它的缺

点是效率低下。

1、算法原理

1）从表中的最后一个记录开始，逐个进行记录的关键字与给定值进行比较，若某个记录的关

键字与给定值相等，则查找成功，找到所查的记录；

2）反之，若直到第一个记录，其关键字和给定值比较都不相等，则表明表中没有所查的记

录，查找失败。

2、算法分析

顺序查找的平均查找长度（Average Search Length，ASL）为(n+1)/2，当查找不成功时，需

要n+1次比较，时间复杂度为O(n);

3、算法实现

/*
  顺序查找。
*/

#include <iostream>
#include <stdio.h>

int SequenceSearch( int *array, int n, int key )
{
  if( array == NULL || n < 0 )
  {
    printf( "invalid input.\n" );
    return -1;
  }
  int i ;
  array[ 0 ] = key;
  
  for( i = n; array[ i ] != array[ 0 ]; i-- )
  {
    if( array[ i ] == key )
      break;
  }
  if( i == 0 )
    return 0;
  else
    return i;
}

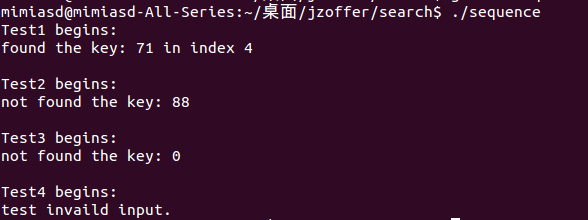
void Test( const char* testName, int* array, int n, int key )
{
  if( testName == NULL ) 
  {
    printf( "test invaild input.\n" );
    return;
  }

  printf( "%s begins: \n", testName );

  if( array == NULL )
  {
    printf( "test invaild input.\n" );
    return;
  }

  int found = SequenceSearch( array, n, key );

  if( found != 0 )
    printf( "found the key: %d in index %d\n", key, found );
  else
    printf( "not found the key: %d\n", key );

  printf( "\n" );
}

// 要找的数字存在
void Test1()
{
  int array[ ] = { 0, 42, 24, 61, 71, 11, 57 };
  Test( "Test1", array, 6, 71 ); 
}

// 要找的数字不存在
void Test2()
{
  int array[ ] = { 0, 421, 24, 6,421, 121, 54 };
  Test( "Test2", array, 6, 88 ); 
}


// 输入数组为空
void Test3()
{
  int emptyArray[ ] = { };
  Test( "Test3", emptyArray, 0, 0 ); 
}

// 输入数组为null，且长度异常
void Test4()
{
  Test( "Test4", NULL, -1, -999 ); 
}

int main()
{
  Test1();
  Test2();
  Test3();
  Test4();

  return 0;
}

二、二分查找

二分查找又称折半查找，优点是比较次数少，查找次数快，平均性能好;其缺点是要求待查表

为有序表，且插入删除困难。因此，折半查找方法使用于不经常变动而查找频繁的有序列表。

首先，假设表中元素是升序排列的，将表中间位置记录的关键字与查找关键字比较，如果两者

相等，则查找成功;否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键

字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到

找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

1、算法原理

要求：1）必须采用顺序储存结构。2）必须按关键字大小有序排列。

基本思想：

1）将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；

2）如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜

索x.

2、算法分析

总共有n个元素，渐渐跟下去就是n,n/2,n/4,....n/2^k（接下来操作元素的剩余个数），其中k就

是循环的次数由于你n/2^k取整后>=1即令n/2^k=1可得k=log2n,（是以2为底，n的对数）所以时

间复杂度可以表示O()=O(logn)。

3、算法实现

/*
  二分查找。
*/

#include <iostream>
#include <stdio.h>

int BinarySearch( int *array, int start, int end, int key )
{
  int left, mid, right;
  
  bool found = false; // 判断是否找到

  left = start;
  right = end;
  
  while( left <= right )
  {
    mid = ( left + right ) / 2;

    if( key == array[ mid ] )
    {
      found = true;
      break;
    }
    else if( key < array[ mid ] )
      right = mid - 1;
    else if( key > array[ mid ] )
      left = mid + 1;
  }
  
  if( found )
    return mid;
  else
    return -1;
}

void Test( const char* testName, int* array, int start, int end, int key )
{
  if( testName == NULL ) 
  {
    printf( "test invaild input.\n" );
    return;
  }

  printf( "%s begins: \n", testName );

  if( array == NULL )
  {
    printf( "test invaild input.\n" );
    return;
  }

  int found = BinarySearch( array, start, end, key );

  if( found >= 0  )
    printf( "found the key: %d in index %d\n", key, found );
  else
    printf( "not found the key: %d\n", key );

  printf( "\n" );
}

// 要找的数字存在
void Test1()
{
  int array[ ] = { 11, 24, 42, 56, 71, 96 };
  Test( "Test1", array, 0, 5, 71 ); 
}

// 要找的数字不存在
void Test2()
{
  int array[ ] = { 21, 24, 46, 56, 72, 82 };
  Test( "Test2", array, 0, 5, 88 ); 
}


// 输入数组为空
void Test3()
{
  int emptyArray[ ] = { };
  Test( "Test3", emptyArray, 0, 0, 0 ); 
}

// 输入数组为null，且长度异常
void Test4()
{
  Test( "Test4", NULL, -1, -1, -999 ); 
}

int main()
{
  Test1();
  Test2();
  Test3();
  Test4();

  return 0;
}

三、分块查找

分块查找是折半查找和顺序查找的一种改进方法，分块查找由于只要求索引表是

有序的，对快内结点没有排序要求，因此特别适合结点动态变化的情况。当增加或减

少节以及节点的关键码改变时，只需将该节点调整到所在的块即可。在空间复杂性上，分块查

找的主要代价是增加了一个辅助数组。需要注意的是，当节点变化很频繁时，可能会导致块与

块之间的节点数相差很大，没写快具有很多节点，而另一些块则可能只有很少节点，这将会导

致查找效率的下降。

分块查找要求把一个大的线性表分解成若干块，每块中的节点可以任意存放，但块与块之间

必须排序。假设是按关键码值非递减的，那么这种块与块之间必须满足已排序要求，实际上就

是对于任意的i，第i块中的所有节点的关键码值都必须小于第i+1块中的所有节点的关键码值。

此外，还要建立一个索引表，把每块中的最大关键码值作为索引表的关键码值，按块的顺序存

放到一个辅助数组中，显然这个辅助数组是按关键码值费递减排序的。查找时，首先在索引表

中进行查找，确定要找的节点所在的块。由于索引表是排序的，因此，对索引表的查找可以采

用顺序查找或折半查找；然后，在相应的块中采用顺序查找，即可找到对应的节点。

1、算法原理

1）先选取各块中的最大关键字构成一个索引表;

2）查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中，然

后在以确定的快中用顺序法进行查找。

2、算法分析

分块查找的平均查找长度由两部分组成，一个是对索引表进行查找的平均查找长度，一个是

对快内节点进行查找的平均查找长度，总的平均查找长度为 E(n)=+。线性表中共有n个节点，

分成大小相等的b块，每块有s=n/b个节点。假定读索引表也采用顺序查找，只考虑查找成功的

情况，并假定对每个节点的查找概率是相等的，则对每块的查找概率是1/b，对快内每个节点的

查找概率是1/s。查找速度介于顺序查找O(n)和折半查找O(logn)之间。

3、算法实现

/*
  分块查找。
*/

#include <iostream>
#include <stdio.h>

struct indexBlock  // 定义块的结构
{
  int key;
  int start;
  int end;
};  // 定义结构体数组

int BlockSearch( int *array, int length, int gap, int key )
{
  if( array == NULL || length <= 0 || gap <= 0 )
  {
    printf( "invalid input.\n" );
    return -1;
  }

  int i = 0;
  int j;
  int begin = -1;
  int k;

  int nBlock = length / gap; 
  
  if( nBlock * gap < length )
    nBlock++;  

  indexBlock block[ nBlock ];  // 数组分为nBlock块

  for( k = 0; k < nBlock; k++ )
  {
    block[ k ].start = begin + 1;  // 确定每个块范围的起始值
    begin++;
  
    block[ k ].end = begin + length / nBlock - 1;  // 确定每个块范围的结束值
    begin += ( length / nBlock - 1 );
    
    if( k < nBlock - 1 )
      block[ k ].key = array[ begin ];  // 确定每个块范围中元素的最大值
    else
      block[ k ].key = array[ length - 1 ]; // 确定最后一块中元素的最大值
  }

  while( i < nBlock && key > block[ i ].key )  // 确定在哪个块中
  {
    i++;
  }

  if( i >= nBlock )   // 大于分的块数，则返回-1,找不到该数
    return -1;
 
  j = block[ i ].start;  // j等于块范围的起始值
  
  while( j <= block[ i ].end && array[ j ] != key )  // 在确定的块内进行查找
  {
    j++;
  }

  if( j > block[ i ].end )  // 如果大于块范围的结束值，则说明没有要查找的数，j置为-1
  {
    j = -1; 
  }

  return j;
}

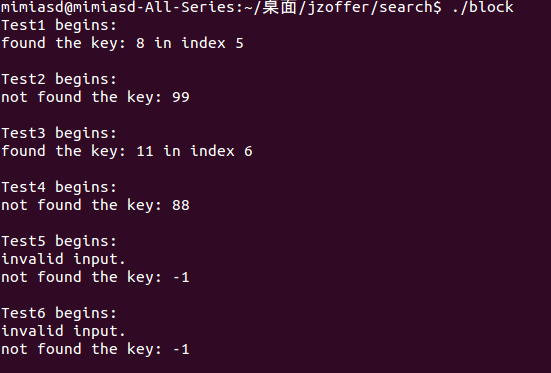
void Test( const char* testName, int* array, int length, int gap, int key )
{
  if( testName == NULL ) 
  {
    printf( "test invaild input.\n" );
    return;
  }

  printf( "%s begins: \n", testName );

  int found = BlockSearch( array, length, gap, key );

  if( found >= 0 )
    printf( "found the key: %d in index %d\n", key, found );
  else
    printf( "not found the key: %d\n", key );

  printf( "\n" );
}

// 要找的数字存在,12个元素分为3组，每组刚好4个元素
void Test1()
{
  int array[ ] = { 5, 3, 6, 7, 9, 8, 11, 15, 18, 20, 40, 50 };
  Test( "Test1", array, 12, 4, 8 ); 
}

// 要找的数字不存在，12个元素分为3组，每组刚好4个元素
void Test2()
{
  int array[ ] = { 5, 3, 6, 7, 9, 8, 11, 15, 18, 20, 40, 50 };
  Test( "Test2", array, 12, 4, 99 ); 
}

// 要找的数字存在，10个元素分为3组，前两组4个元素，最后一组2个元素
void Test3()
{
  int emptyArray[ ] = { 5, 3, 6, 7, 9, 8, 11, 15, 18, 20 };
  Test( "Test3", emptyArray, 10, 4, 11 ); 
}

// 要找的数字不存在，10个元素分为3组，前两组4个元素，最后一组2个元素
void Test4()
{
  int emptyArray[ ] = { 5, 3, 6, 7, 9, 8, 11, 15, 18, 20 };
  Test( "Test4", emptyArray, 10, 4, 88 ); 
}

// 输入数组为空
void Test5()
{
  int emptyArray[ ] = { };
  Test( "Test5", emptyArray, 0, 0, -1 ); 
}

// 输入数组为null，且长度异常
void Test6()
{
  Test( "Test6", NULL, -1, 0, -1 ); 
}

int main()
{
  Test1();
  Test2();
  Test3();
  Test4();
  Test5();
  Test6();

  return 0;
}

四、哈希查找

哈希查找是通过计算数据元素的存储地址进行查找的一种方法。我们使用一个下标范围比较

大的数组来存储元素。可以设计一个函数（哈希函数，也叫做散列函数），使得每个元素的关

键字都与一个函数值（即数组下标）相对应，于是用这个数组单元来存储这个元素；也可以简

单的理解为，按照关键字为每一个元素"分类"，然后将这个元素存储在相应"类"所对应的地方。

但是，不能够保证每个元素的关键字与函数值是一一对应的，因此极有可能出现对于不同的元

素，却计算出了相同的函数值，这样就产生了"冲突"，换句话说，就是把不同的元素分在了相同

的"类"之中。

1、算法原理

哈希查找步骤：

1）用给定的哈希函数构造哈希表；

2）根据选择的冲突处理方法解决地址冲突；

3）在哈希表的基础上执行哈希查找。

建立哈希表操作步骤：

1）取数据元素的关键字key，计算其哈希函数值。若该地址对应的存储空间还没有被占用，则

将该元素存入；否则执行step2解决冲突。

2）根据选择的冲突处理方法，计算关键字key的下一个存储地址。若下一个存储地址仍被占

用，则继续执行step2，直到找到能用的存储地址为止。

哈希查找步骤为：

1）Step1 对给定k值，计算哈希地址 Di=H（k）；若HST为空，则查找失败；若HST=k，则查

找成功；否则，执行step2（处理冲突）。

2）Step2 重复计算处理冲突的下一个存储地址 Dk=R（Dk-1），直到HST[Dk]为空，或

HST[Dk]=k为止。若HST[Dk]=K，则查找成功，否则查找失败。

2、算法分析

时间复杂度几乎是O(1)，取决于产生冲突的多少。

3、算法实现

/*
  哈希查找。实现哈希函数为“除法取余法”，解决冲突为“开放地址线性探测法”。
--除法取余法：key=value%C;
--开放地址线性探测法：如果两个数据元素的哈希值相同，则在哈希表中为后插入的数据元素另外选择一个表项。当程序查找哈希表时，
  如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素，程序就会继续往后查找，直到找到一个符合查找要求的数据元素，
  或者遇到一个空的表项。　
*/

#include <iostream>
#include <stdio.h>

void InsertHash( int *hashArray, int length, int data )
{
  int hashAddress = data % length; // 哈希函数
  
  while( hashArray[ hashAddress ] != 0 )  // 如果key存在，则说明已经被别人占用，此时必须解决冲突,这里假设哈希表元素都初始化为0,而插入元素都大于0
  {
    hashAddress = ( ++hashAddress ) % length;  // 用开放寻址法找到
  }

  hashArray[ hashAddress ] = data;
}

int HashSearch( int *hashArray, int length, int key )
{
  if( hashArray == NULL || length <= 0 )
  {
    printf( "invalid input.\n" );
    return -1;
  }
  
  int hashAddress = key % length;

  while( hashArray[ hashAddress ] != 0 && hashArray[ hashAddress ] != key )
  {
    hashAddress = ( ++hashAddress ) % length;
  }

  if( hashArray[ hashAddress ] == 0 )
    return -1;
  else
    return hashAddress;
}

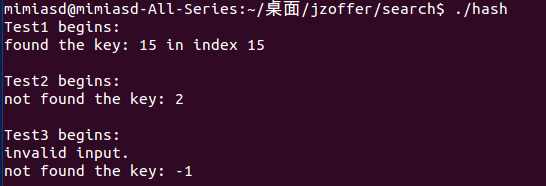
void Test( const char* testName, int* hashArray, int length, int key )
{
  if( testName == NULL ) 
  {
    printf( "test invaild input.\n" );
    return;
  }

  printf( "%s begins: \n", testName );

  int found = HashSearch( hashArray, length, key );

  if( found >= 0 )
    printf( "found the key: %d in index %d\n", key, found );
  else
    printf( "not found the key: %d\n", key );

  printf( "\n" );
}

// 要找的数字存在,数组12个元素，哈希表的大小选为离数组大小二倍最近的质数，这里是29
void Test1()
{
  int length = 29;
  int arrayLength = 12;
  int array[ ] = { 5, 3, 6, 7, 9, 8, 11, 15, 18, 20, 40, 50 };

  int *hash = new int[ length ];
  
  for( int i = 0; i < length; i++ )
  {
    hash[ i ] = 0;    // 初始化哈希表元素为0
  }
  
  for( int j = 0; j < arrayLength; j++ )
  {
    InsertHash( hash, length, array[ j ] );
  }

  Test( "Test1", hash, length, 15 ); 

  delete [] hash;
}

// 要找的数字不存在,数组12个元素，哈希表的大小选为离数组大小二倍最近的质数，这里是29
void Test2()
{
  int length = 29;
  int arrayLength = 12;
  int array[ ] = { 5, 3, 6, 7, 9, 8, 11, 15, 18, 20, 40, 50 };

  int *hash = new int[ length ];
  
  for( int i = 0; i < length; i++ )
  {
    hash[ i ] = 0;    // 初始化哈希表元素为0
  }
  
  for( int i = 0; i < arrayLength; i++ )
  {
    InsertHash( hash, length, array[ i ] );
  }

  Test( "Test2", hash, length, 2 ); 

  delete [] hash;
}

// 输入数组为null，且长度异常
void Test3()
{
  Test( "Test3", NULL, -1, -1 ); 
}

int main()
{
  Test1();
  Test2();
  Test3();
  
  return 0;
}