网络流不要算复杂度,远远达不到上界。但注意控制点数。
普通最大流可以处理无下界有上界的问题
最小割通常要找到性质转化为二分图。
常见转化:
要求“至少”下界但没有上界,求“最小”。反一下。先满足所有要求,再最吝啬地拿走“最大流”。
例题
《士兵占领》:行列是独立的点集,在点放兵相当于在两个集间连边。反一下走流量就成了在该行该列同时减人,跑最大流即可。
拆点:很实用的思想,也很不好想。
如果$x1$在$Y$的操作对后面有影响,或$x$的顺序影响$Y$的贡献,且影响不能通过流量和费用表示出来,那么就可把$Y$拆成多个点,表示在某尺度上的差别。
例题
《紧急疏散evacuate》:一个人通过会在同一时间同一出口后卡住后面的人,而后面的人依旧可以被鸽到下一秒,所以把门拆成k个点,t向t+1连inf边。
《修车》:最小平均即求最小总时间,倒数第i个修有贡献i*t(让自己和后边的人都等了t),这个转化很妙。对于修的顺序有不同费用,所以对人和车的关系拆点(权值乘上倒数系数),跑最小费用最大流。
最小割:
结论:最小割等于最大流
非板子,一般要找到二分图的性质。也就是说图不能太“长”。
常见模型:
多叉戟:选点有花费,点集有收益。(可以处理两种选择)
$|V|$和$|E|$都是m级别

inf边表示连通必不能割。
记总收益$sum=\sum\limits_{i=1}^{m} w_i$。
割掉c代表为了保留(获得)w付出相应的代价,割掉w表示代价太高那不要收益。
综上用$ans=sum-maxflow$
例题:
《最大获利》:直接建三叉戟就行。
《happiness》:同时的关系要表现在同时割掉两个单边那么就要保留一个复合边,通过思考瞎试有下复合三叉戟结构
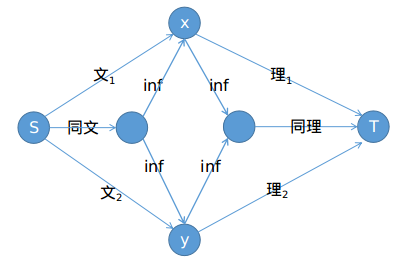
感觉没有什么规律,更多的是在试。。。
《employ人员雇佣》:咕