地址 http://poj.org/problem?id=2991




题解
本来以为这是一个简单的线段树模板 不料始终不太明白线段树如何记录转动角度后的各个线段端的XY值
学习了网络上的一些博客题解 感觉似是而非 谈到复数 角度 向量等,有点不太好理解
现在这里将自己的理解记录如下
如图
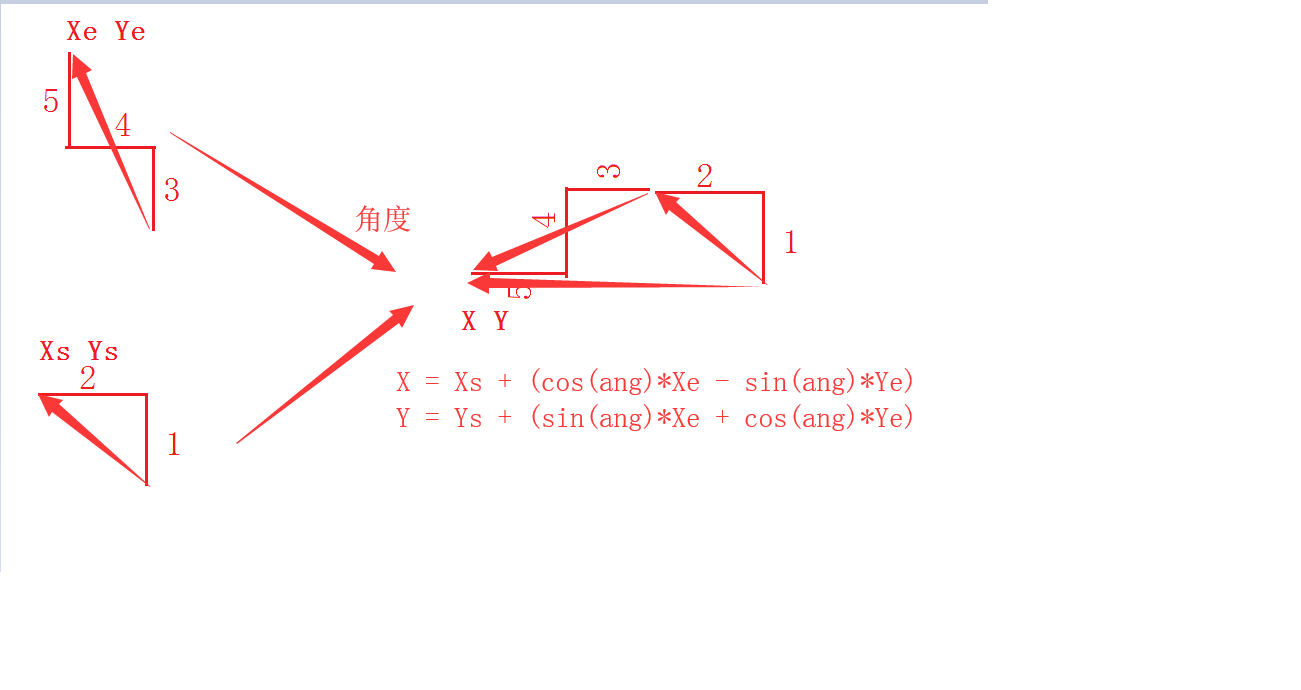
1 预备知识
使用线段树记录的内容如下 指示某段线段的组合 以第一条线段为垂直 最后的线段的端点的X Y值
途中1~2 线段 和3~5线段 就是线段树节点1~5的子节点 那么线段树节点1~5 就记录1~5结合后的X Y 值以及两个子节点结合的角度值
由于3~5线段的XY 是以自己的第一条线段为垂直起点为0 0 计算出来的X Y
那么在于1~2线段合并的时候 并不是简单的将两子节点的X Y相加即可得到1~5线段的XY 而是要加入旋转了相对角度 该角度由记录1~5线段的线段树节点记录
1~2线段部分的X Y值 旋转相对角度的公式推导如下
https://blog.csdn.net/hjq376247328/article/details/45113563
其实也就是
xNew = x * cosB - y * sinB
yNew = x * sinB + y * cosB
再来和 1~2线段的X Y相加即可得到1~5线段的X Y,并将该两子节点的相对角度记录在父节点中
预备知识讲完
2 解答步骤如下
一 建造线段树 build(1,1,n); 由于每条线段都是垂直连接 所以X 均为0 相对角度全部为0
void build(int k,int l,int r) {
angT[k]=x[k]=0.0;
if(r==l) y[k]=L[l];
else {
int lson=k*2, rson=k*2+1;
int m=(l+r)/2;
build(lson,l,m);
build(rson,m+1,r);
y[k]=y[lson]+y[rson];
}
}
二 某段线段转动角度后
题意输入的角度是si和si+1逆时针角度而不是旋转的角度,而是需要转到的结果角度, 所以我们需要进行转换 。所以使用了pre数组记录每段线段与相邻线段的逆时针间隔角度,这样接收到题意输入角度a后
a-pre[s] 就是实际要转动的角度 而且需要更新pre[s] 以便下次计算
change(s,ang-pre[s],1,1,n); pre[s]=ang; // 要求改变为a度 考虑之前已改变过
chang()代码就是批量更新需要转换的角度和X Y
只有旋转的起点线段在当前线段树节点的左子节点 我们才更新当前线段树节点的角度记录
如图
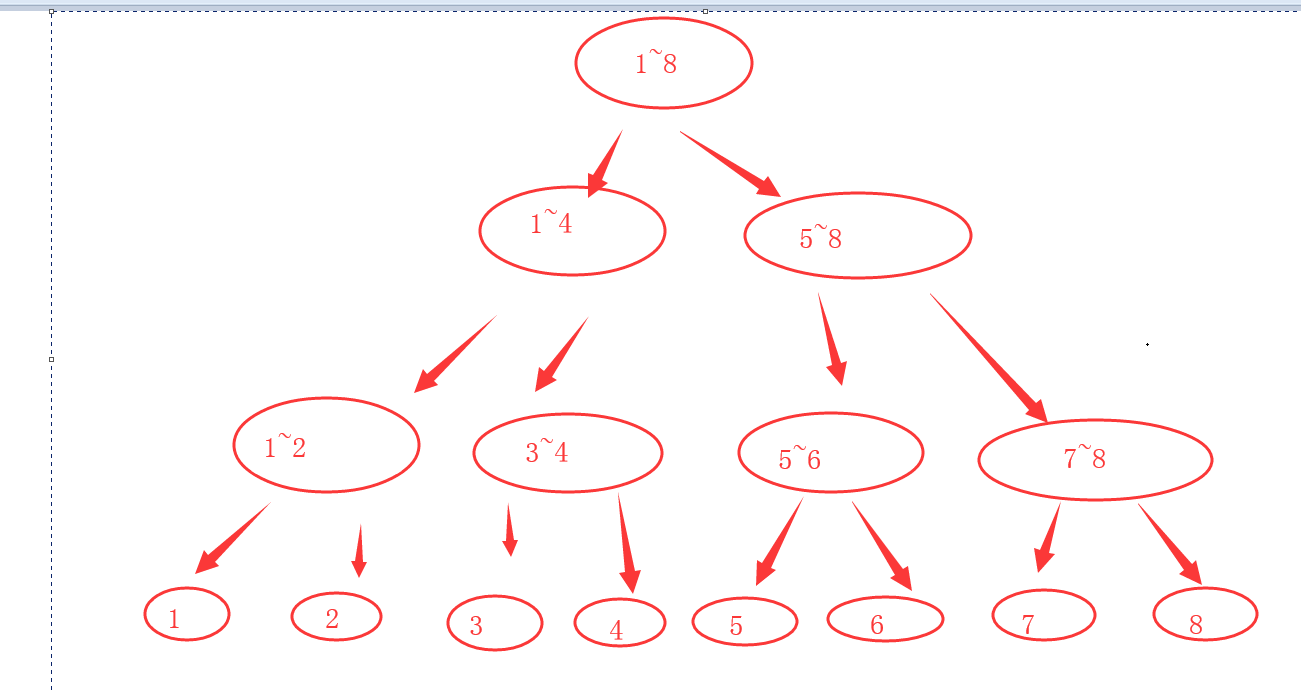
假设节点4 向3旋转90度
那么合并1 2的时候无更新
合并3 4的时候 3~4节点的角度要在原来记录上再旋转90
合并1~2 3~4为1~4的时候无需更新角度 因为 3~4 已经旋转 与1 ~2的相对角度 并没有变化
同样 5~8节点流程中无变化
但是合并1~4 5~8节点的时候 角度需要旋转90
整个流程下来 4 5~8 角度均旋转更新1次 符合题目的集合意义
最后返回1~8节点记录的X Y即可
代码如下
#include <iostream>
#include <vector>
#include <math.h>
#include <stdio.h>
using namespace std;
const double PI=acos(-1.0);
const int N=10005;
int n,c,L[N];
double pre[N];
double angT[N<<2];
double x[N<<2],y[N<<2];
void build(int k,int l,int r) {
angT[k]=x[k]=0.0;
if(r==l) y[k]=L[l];
else {
int lson=k*2, rson=k*2+1;
int m=(l+r)/2;
build(lson,l,m);
build(rson,m+1,r);
y[k]=y[lson]+y[rson];
}
}
void change(int s,double ang,int k,int l,int r) {
if(s<l || l==r) return; // 操作位置不在范围内 或 区间长度为1 不作处理
else if(s<=r) {
int lson=k*2, rson=k*2+1;
int m=(l+r)/2;
change(s,ang,lson,l,m);
change(s,ang,rson,m+1,r); // 先处理左右子区间
if(s<=m) angT[k]+=ang; // 操作位置位于区间的左子区间内 可根据左右子区间的向量更新
double sina=sin(angT[k]), cosa=cos(angT[k]);
x[k]=x[lson]+(x[rson]*cosa-y[rson]*sina);
y[k]=y[lson]+(x[rson]*sina+y[rson]*cosa);
}
}
int main()
{
while(~scanf("%d%d",&n,&c)) {
for(int i=1;i<=n;i++) {
scanf("%d",&L[i]);
pre[i]=PI;
}
build(1,1,n);
while(c--) {
int s,a; scanf("%d%d",&s,&a);
double ang=(double)a/180.0*PI;
change(s,ang-pre[s],1,1,n);
pre[s]=ang; // 要求改变为a度 考虑之前已改变过
printf("%.2f %.2f\n",x[1],y[1]);
}
printf("\n");
}
return 0;
}