抛物线

抛物线的定义

抛物线的定义

平面内，到定点\(F\)的距离与到定直线\(l\)的距离相等的点的轨迹叫抛物线，其中定点\(F\)不在定直线\(l\)上.

抛物线的相关概念

焦点：定点\(F\);
准线：定直线\(l\);
焦准距：定点\(F\)到定直线\(l\)的距离.

抛物线的标准方程

在\(x\)轴：\(y^2=2px(p\neq 0)\)
在\(y\)轴：\(x^2=2py(p\neq 0)\)

抛物线的性质

对称性

关于坐标轴对称

顶点

原点

范围

\(x\geq 0;x\leq 0;y\geq 0;y\leq 0.\)

离心率

\(e=1\)

通经

过焦点垂直\(x\)轴的弦，长为\(2p\)

焦半径

抛物线上一点\(P(x_0,y_0)\)到焦点所连线段，长为\(x_0+\frac{p}{2}\)；\(y_0+\frac{p}{2}\);\(-x_0+\frac{p}{2}\);\(-y_0+\frac{p}{2}\)

焦点弦

过焦点的直线与抛物线截得线段.

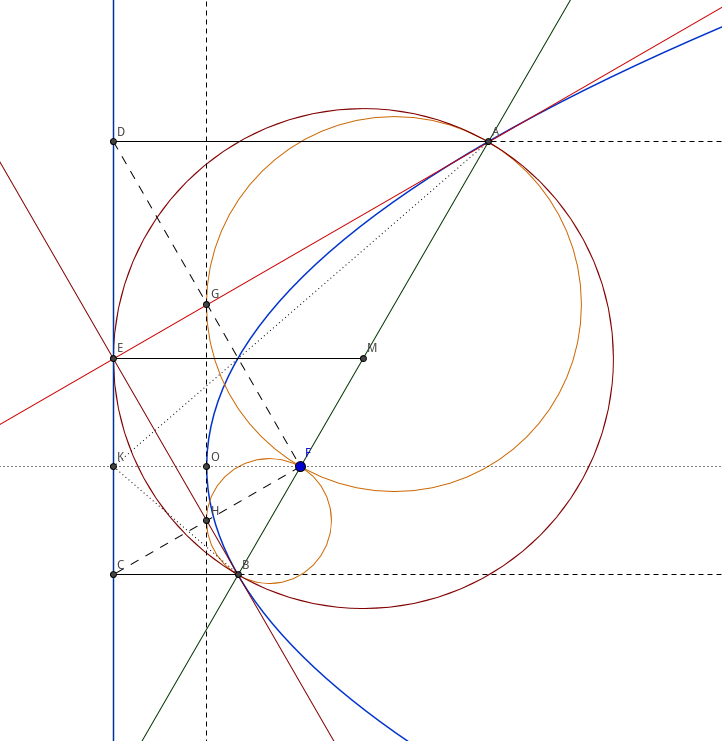
焦点弦性质，如图

①\(AE\bot BE,EF\bot AB,DF\bot CF\)

②\(\angle AKF=\angle BKF\)

③以为\(AB\)直径的圆与准线相切

④\(|AF|=\dfrac{p}{1-\cos \theta},|BF|=\dfrac{p}{1+\cos \theta}\)

⑤\(|AB|=x_1+x_2+p=\dfrac{2p}{\sin^2 \theta}\)

⑥\(\dfrac{1}{|AF|}+\dfrac{1}{|BF|}=\dfrac{2}{p}\)

⑦\(y_1y_2=-p^2,x_1x_2=\dfrac{p^2}{4},|y_1-y_2|=\dfrac{2p}{\sin \theta}\)

⑧\(k_{OA}\cdot k_{OB}=-4,\overrightarrow{OA}\cdot\overrightarrow{OB}=-\dfrac{3}{4}p^2\)

⑨\(S_{\triangle AOB}=\dfrac{p^2}{2\sin \theta}\)

来源：https://www.cnblogs.com/chenshu-09/p/11977399.html