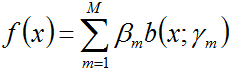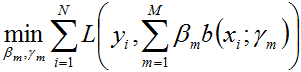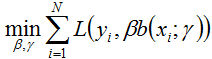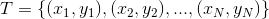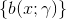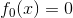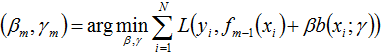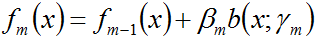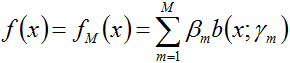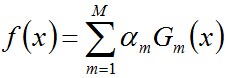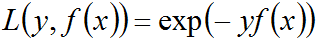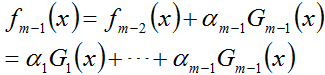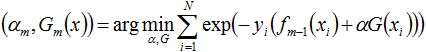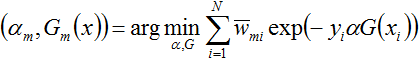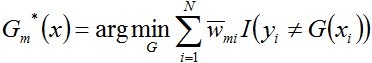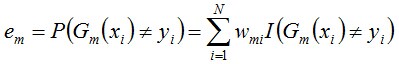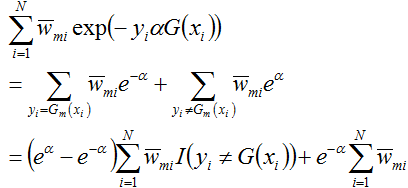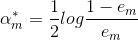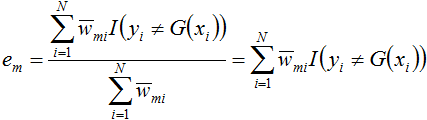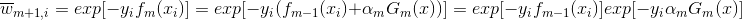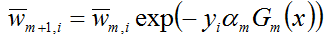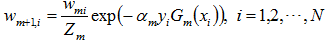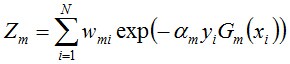加法模型和前向分布算法
如下图所示的便是一个加法模型
其中，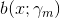
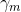
称为基函数，
称为基函数的参数，
称为基函数的系数。
在给定训练数据及损失函数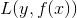
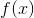
的条件下，学习加法模型
成为经验风险极小化问题，即损失函数极小化问题：
随后，该问题可以作如此简化：从前向后，每一步只学习一个基函数及其系数，逐步逼近上式，即：每步只优化如下损失函数：
这个优化方法便就是所谓的前向分步算法。
下面，咱们来具体看下前向分步算法的算法流程：
- 输入：训练数据集
- 损失函数：
- 基函数集：
- 输出：加法模型
- 算法步骤：
- 1. 初始化
- 2. 对于m=1,2,..M
- a)极小化损失函数
- 1. 初始化
得到参数
- b)更新
- 3. 最终得到加法模型
就这样，前向分步算法将同时求解从m=1到M的所有参数（、）的优化问题简化为逐次求解各个、（1≤m≤M）的优化问题。
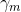
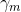
前行分布算法和Adaboost的关系
Adaboost 还有另外一种理解，即可以认为其模型是加法模型、损失函数为指数函数、学习算法为前向分步算法的二类分类学习方法。其实，Adaboost算法就是前向分步算法的一个特例，Adaboost
中，各个基本分类器就相当于加法模型中的基函数，且其损失函数为指数函数。
换句话说，当前向分步算法中的基函数为Adaboost中的基本分类器时，加法模型等价于Adaboost的最终分类器
你甚至可以说，这个最终分类器其实就是一个加法模型。只是这个加法模型由基本分类器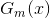
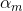
及其系数
组成，m
= 1, 2, ..., M。前向分步算法逐一学习基函数的过程，与Adaboost算法逐一学习各个基本分类器的过程一致。
下面，咱们便来证明：当前向分步算法的损失函数是指数损失函数
时，其学习的具体操作等价于Adaboost算法的学习过程。
假设经过m-1轮迭代，前向分步算法已经得到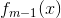
：
而后在第m轮迭代得到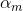
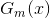
、和
。其中，为：
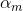
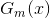
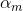
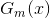
而和未知。所以，现在咱们的目标便是根据前向分步算法训练和，使得最终在训练数据集T上的指数损失最小，即
针对这种需要求解多个参数的情况，可以先固定其它参数，求解其中一两个参数，然后逐一求解剩下的参数。例如我们可以固定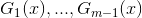
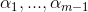
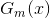
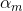
和
，只针对和做优化。
换言之，在面对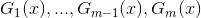
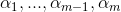
和
这2m个参数都未知的情况下，可以：
- 先假定和已知，求解出和；
- 然后再逐一求解其它未知参数。
且考虑到上式中的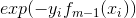
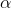
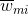
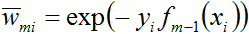
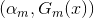
既不依赖
也不依赖G，所以是个与最小化无关的固定值，记为
，即
，则上式可以表示为（后面要多次用到这个式子，简记为
）：
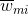
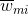
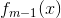
值得一提的是，虽然与最小化无关，但依赖于，随着每一轮迭代而发生变化。
接下来，便是要证使得上式达到最小的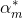
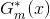
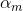
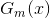
和
就是Adaboost算法所求解得到的和。
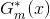
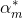
为求解上式，咱们先求再求。
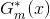
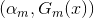
首先求。对于任意
，使上式最小的G(x)由下式得到：
别忘了，。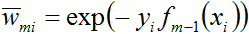
跟1.2节所述的误差率的计算公式对比下：
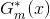
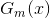
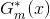
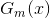
可知，上面得到的便是Adaboost算法的基本分类器，因为它是在第m轮加权训练数据时，使分类误差率最小的基本分类器。换言之，这个便是Adaboost算法所要求的，别忘了，在Adaboost算法的每一轮迭代中，都是选取让误差率最低的阈值来设计基本分类器。
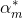
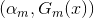
然后求。还是回到之前的这个式子上：
这个式子的后半部分可以进一步化简，得：
接着将上面求得的
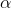
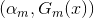
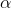
代入上式中，且对求导，令其求导结果为0，即得到使得一式最小的，即为：
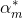
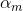
这里的跟上文1.2节中的计算公式完全一致。
此外，毫无疑问，上式中的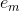
便是误差率：
即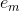就是被Gm(x)误分类样本的权值之和。
就这样，结合模型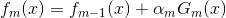
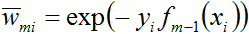
，跟，可以推出
从而有：
与上文1.2节介绍的权值更新公式
相比，只相差一个规范化因子，即后者多了一个
所以，整个过程下来，我们可以看到，前向分步算法逐一学习基函数的过程，确实是与Adaboost算法逐一学习各个基本分类器的过程一致，两者完全等价。
综上，本节不但提供了Adaboost的另一种理解：加法模型，损失函数为指数函数，学习算法为前向分步算法，而且也解释了最开始1.2节中基本分类器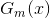及其系数的由来，以及对权值更新公式的解释，你甚至可以认为本节就是对上文整个1.2节的解释。
来源：CSDN
作者：遇见更好的自己
链接：https://blog.csdn.net/yc1203968305/article/details/78171464