20182311 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结

教材学习内容总结
- 教材第十九章
教材学习中的问题和解决过程
代码调试中的问题和解决过程
代码托管
结对及互评
- 点评过的同学博客和代码
上周错题总结
学习进度条
参考链接

正文

教材学习内容总结

教材第十九章

非线性结构——图

基本概念：
- 定义：图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
- 邻接：若图中的两个顶点之间有边连接，那么他们是邻接的。
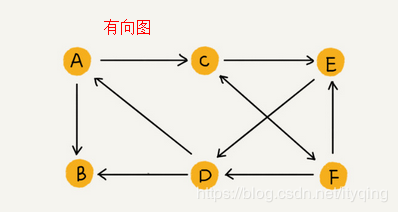
- 有向图（Directed graphs）：图中任意两个顶点之间的边都是有向边。
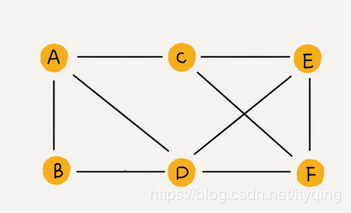
- 无向图（Undirected graphs）：图中任意两个顶点之间的边都没有方向。
- 入度(In-degree) : 表示有多少条边指向这个顶点
- 出度(Out-degre) : 表示有多少条边是以这个顶点为起点推向其他顶点
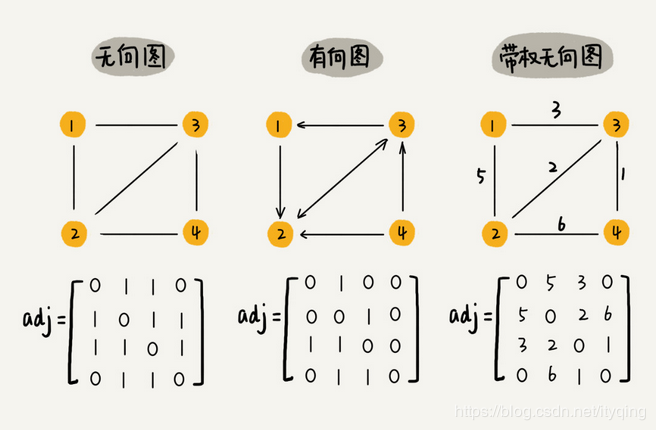
- 带权图：每条边对应一个权值，又称为网络。路径上的权轻易为路径中所含边上的权值之和。
- 最小生成树：所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树。基于带权图实现最小生成树的算法思路如下：

将图各边按照权值进行排序
将图遍历一次，找出权值最小的边，加入最小生成树的集合中。不符合条件则继续遍历图，寻找下一个最小权值的边。
递归重复步骤1，直到找出n-1条边为止（设图有n个结点，则最小生成树的边数应为n-1条），算法结束。得到的就是此图的最小生成树。

图的实现

图的存储结构

邻接矩阵：一个二维数组。用1表示两顶点邻接，0表示两顶点不邻接。若vi-vj有边，则matrix[i][j]=1;无向图的邻接矩阵对称，有向图的不对称。

//构建无向图的邻接矩阵
  public void createUGraph(){
      Scanner in=new Scanner(System.in);
      //构建顶点数组
      System.out.println("请输入顶点：");
      for(int i=0;i<vexnum;i++)
          vexs[i]=in.next().charAt(0);
      //初始化邻接矩阵
      for(int i=0;i<vexnum;i++)
          for(int j=0;j<vexnum;j++)
              matrix[i][j]=0;
      //构建邻接矩阵
      for(int p = 0; p < this.arcnum; p++) {
          System.out.println("请输入每条边的头尾：");
          char a = in.next().charAt(0);
          char b = in.next().charAt(0);
          int i = this.locateVex(a);
          int j = this.locateVex(b);
          this.matrix[i][j] = this.matrix[j][i] = 1; //对称阵
      }
  }
  public int locateVex(char a){
      for(int i=0;i<vexnum;i++){
          if(vexs[i]==a)
              return i;
      }
      return -1;
  }

//构建有向图的邻接矩阵
  public void createGraph(){
      Scanner in=new Scanner(System.in);
      System.out.println("请输入顶点：");
      for(int i=0;i<vexnum;i++)
          vexs[i]=in.next().charAt(0);
      for(int i=0;i<vexnum;i++)
          for(int j=0;j<vexnum;j++)
              matrix[i][j]=0;

      //构建邻接矩阵
      for(int p = 0; p < this.arcnum; p++) {
          System.out.println("请输入每条边的头尾：");
          char a = in.next().charAt(0);
          char b = in.next().charAt(0);
          int i = this.locateVex(a);
          int j = this.locateVex(b);
          this.matrix[i][j]=1;
      }
  }

基于邻接矩阵，计算有向图和无向图的出度和入度

//计算无向图节点的出入度
  public void CalU(int i){
      int count=0;
          for(int j=0;j<vexnum;j++){
              count+=matrix[i][j];
              count+=matrix[j][i];
          }
      System.out.println(vexs[i]+"的出度和入度均为"+count);
  }

//计算有向图节点的出入度
public void Cal(int i){
    int countin=0,countout=0;
        for(int j=0;j<vexnum;j++) {
            countin+=matrix[i][j];
            countout+=matrix[j][i];
}
    System.out.println(vexs[i]+"的出度为"+countout+",入度为"+countin);
}

邻接表：用一个列表方置顶点类，定点类类中留有指向路径类的索引，路径类之间可相互指向。有List类，VexNode类和ArcNode类
```
import java.util.Scanner;

class VexNode {
public char ch;
public ArcNode firstarc;

public VexNode(char data){
this.ch=data;
}
}

class ArcNode {
public int value;
public ArcNode nextarc;

public ArcNode(int value) {
    this.value = value;
}

}
public class GraphList {
public int vexnum;
public int arcnum;
public VexNode[] vexs;

public GraphList(int vexnum, int arcnum) {
    this.vexnum = vexnum;
    this.arcnum = arcnum;
    vexs=new VexNode[vexnum];
}

public void createList(){
    //先存入顶点
    System.out.println("请输入顶点：");
    Scanner in =new Scanner(System.in);
    for(int i=0;i<vexnum;i++)
        vexs[i]=new VexNode(in.next().charAt(0));
    //再存入边及权值
    for(int p = 0; p < this.arcnum; p++) {
        System.out.println("请输入头尾:");
        char a =in.next().charAt(0);
        char b =in.next().charAt(0);
        int i = this.locateVex(a);
        int j = this.locateVex(b);
        ArcNode temp=new ArcNode(j);
        temp.nextarc=vexs[i].firstarc;
        vexs[i].firstarc=temp;
    }
}
public int locateVex(char a){
    for(int i=0;i<vexnum;i++){
        if(vexs[i].ch==a)
            return i;
    }
    return -1;
}

public void Count(int i){
    int count=0;
        if(vexs[i].firstarc!=null){
            ArcNode temp=vexs[i].firstarc;
            count++;
            while(temp.nextarc!=null){
                count++;
                temp=temp.nextarc;
            }
        }
    System.out.println(vexs[i].ch+"的出度为:"+count);
}

}

 
- 图的遍历
  - BFS：从起始点开始，每轮访问与当前点邻接，且未被访问过的顶点，直到所有点被访问完。类似于从湖中心荡开一层层涟漪。
  - DFS：从起始点开始，“一条路走到黑”，若是走到“无路可走”，也就是当前顶点没有邻接点未被访问过时，则返回寻找可走的路。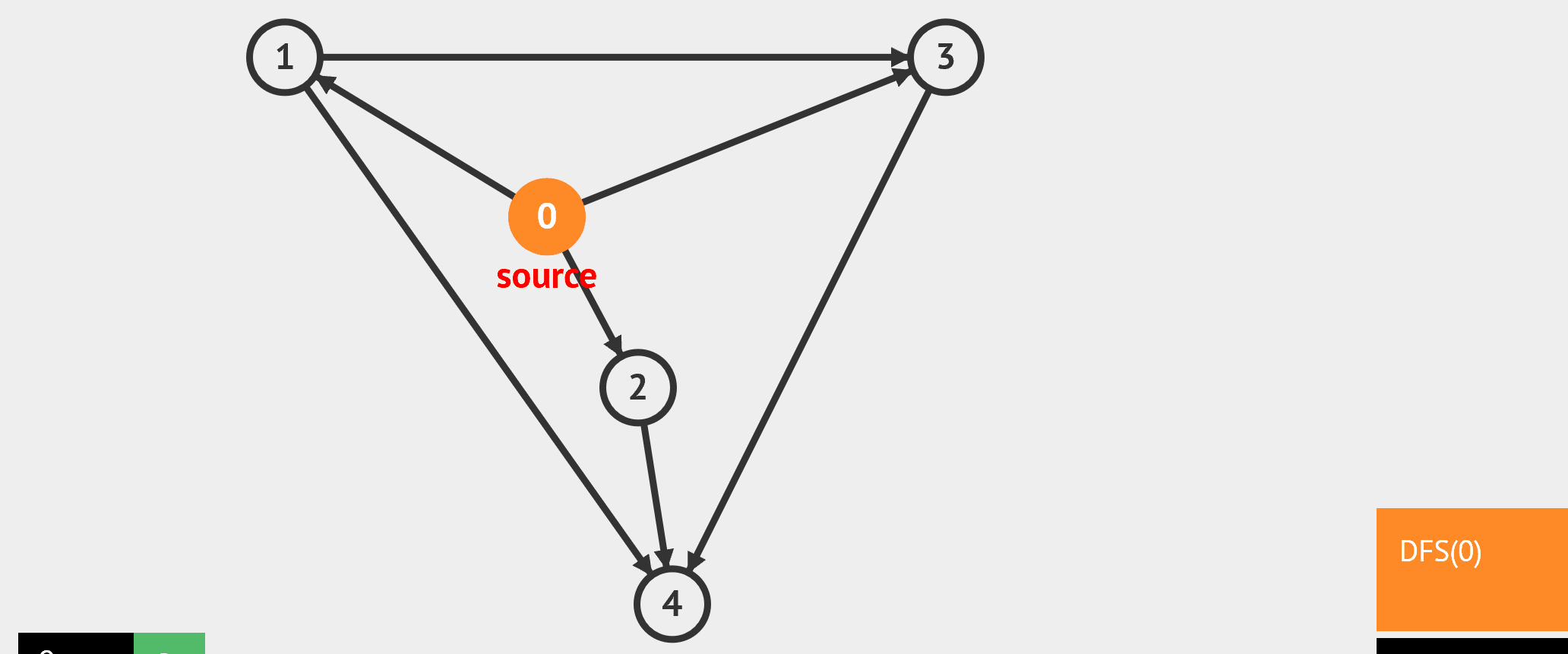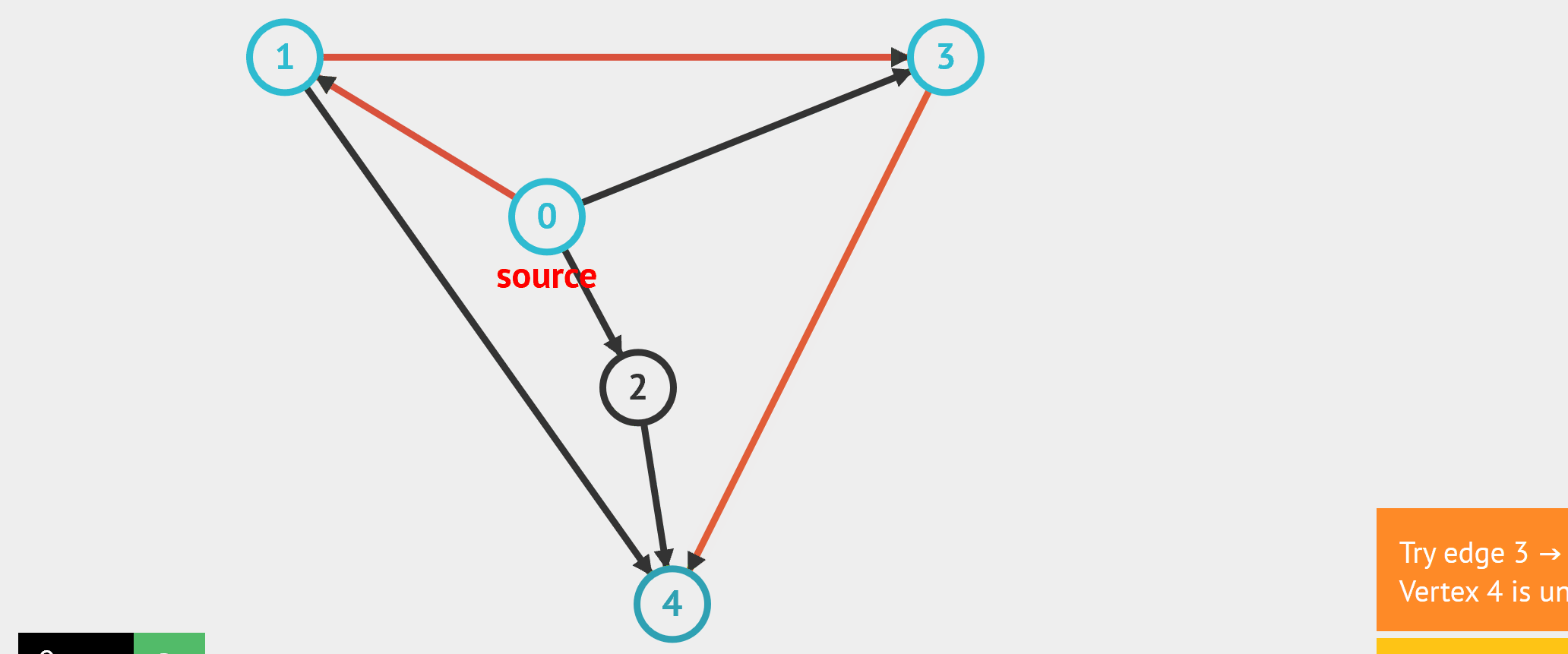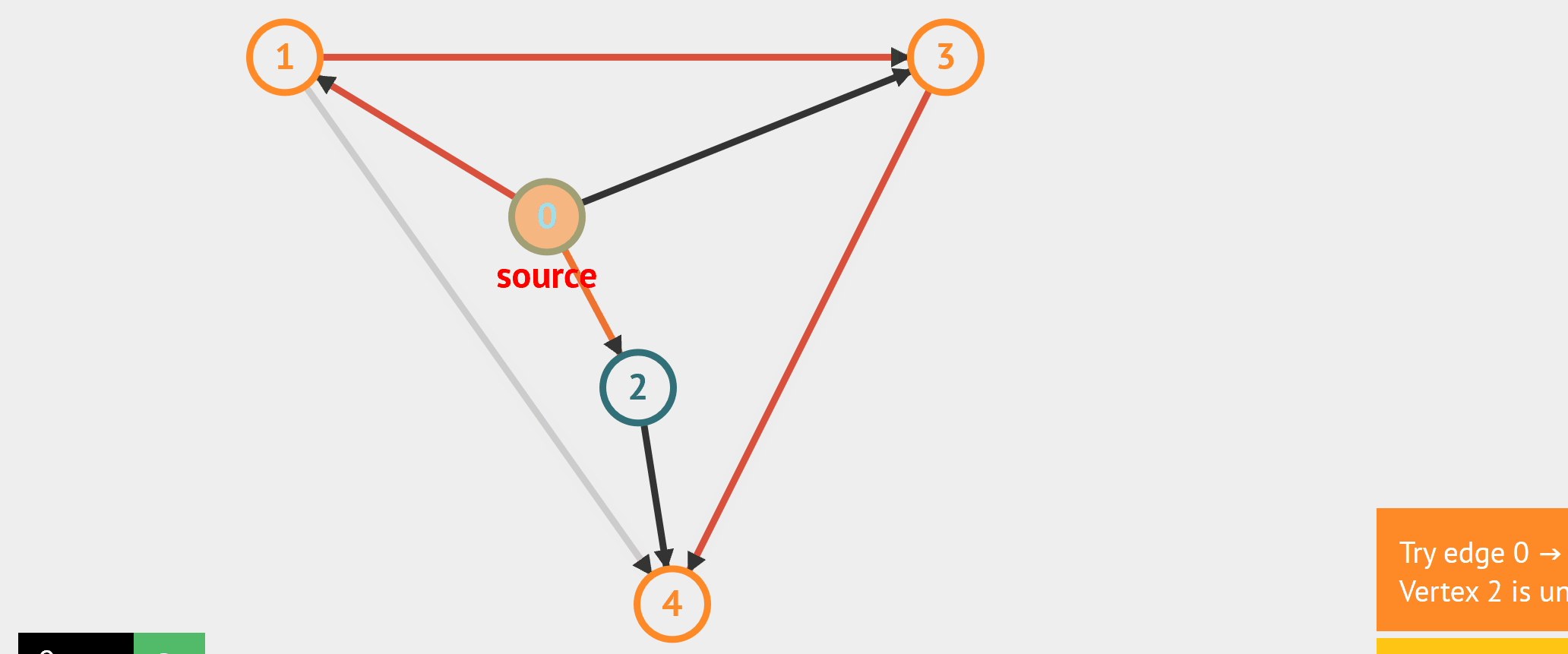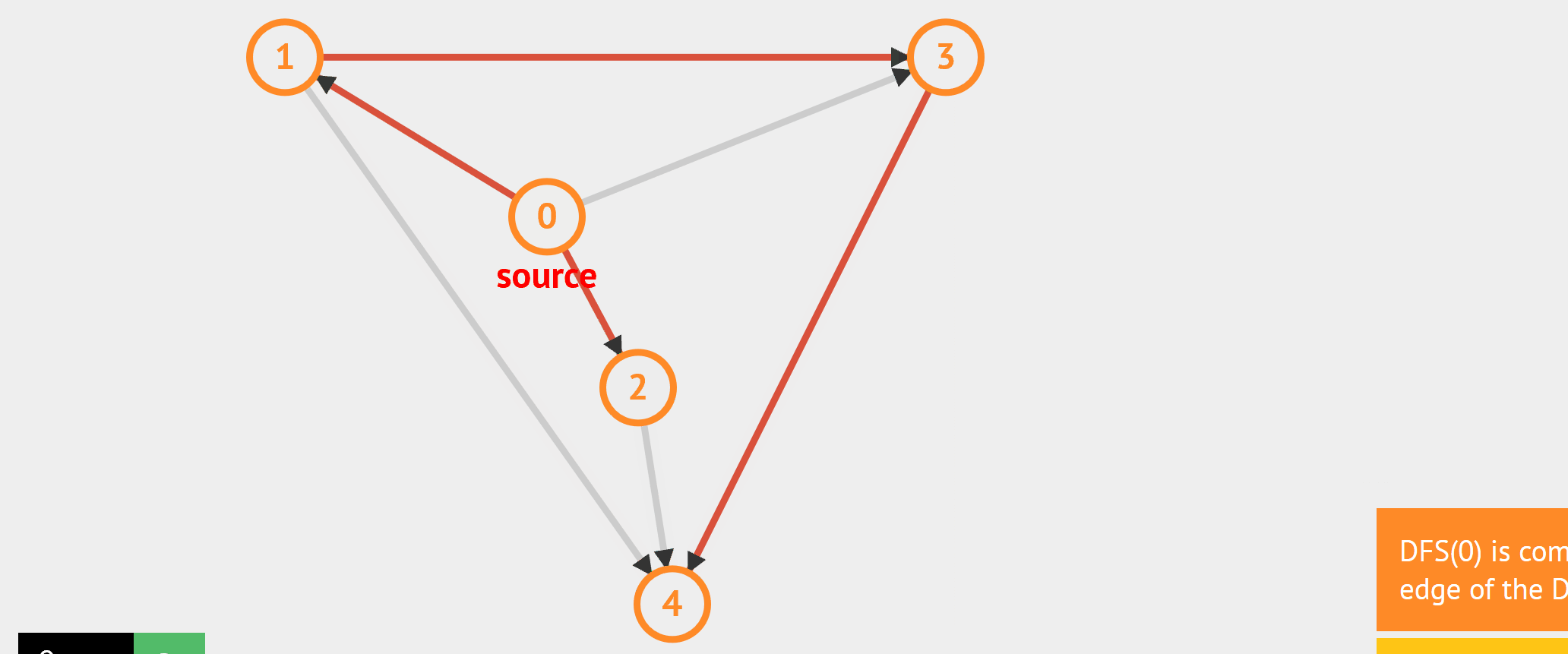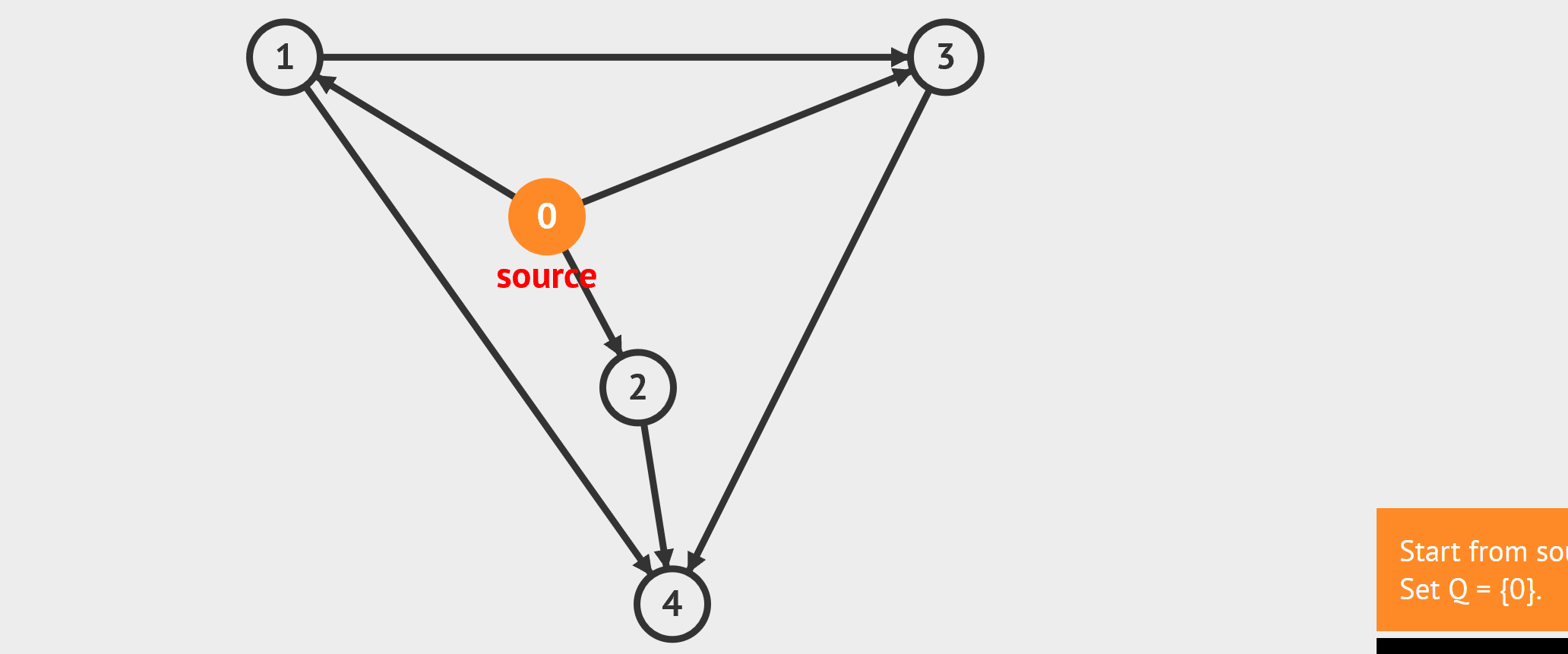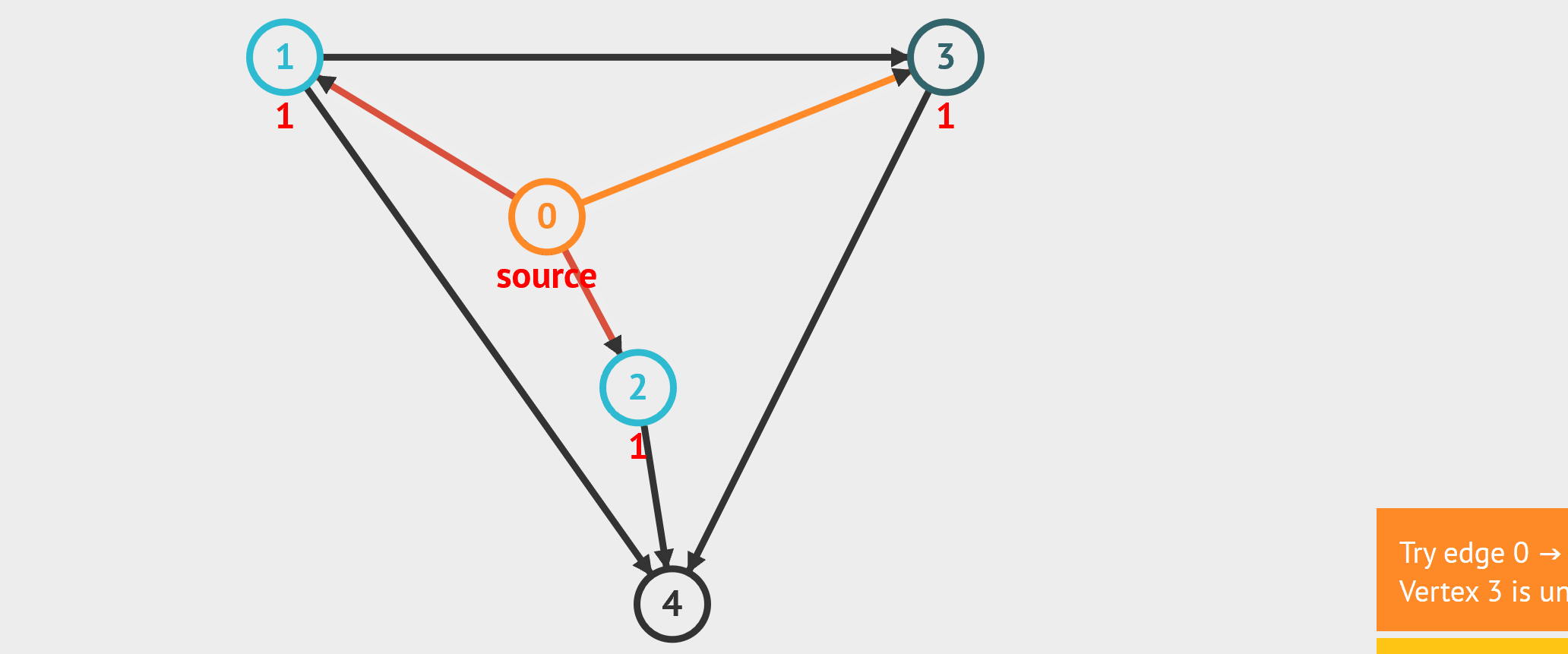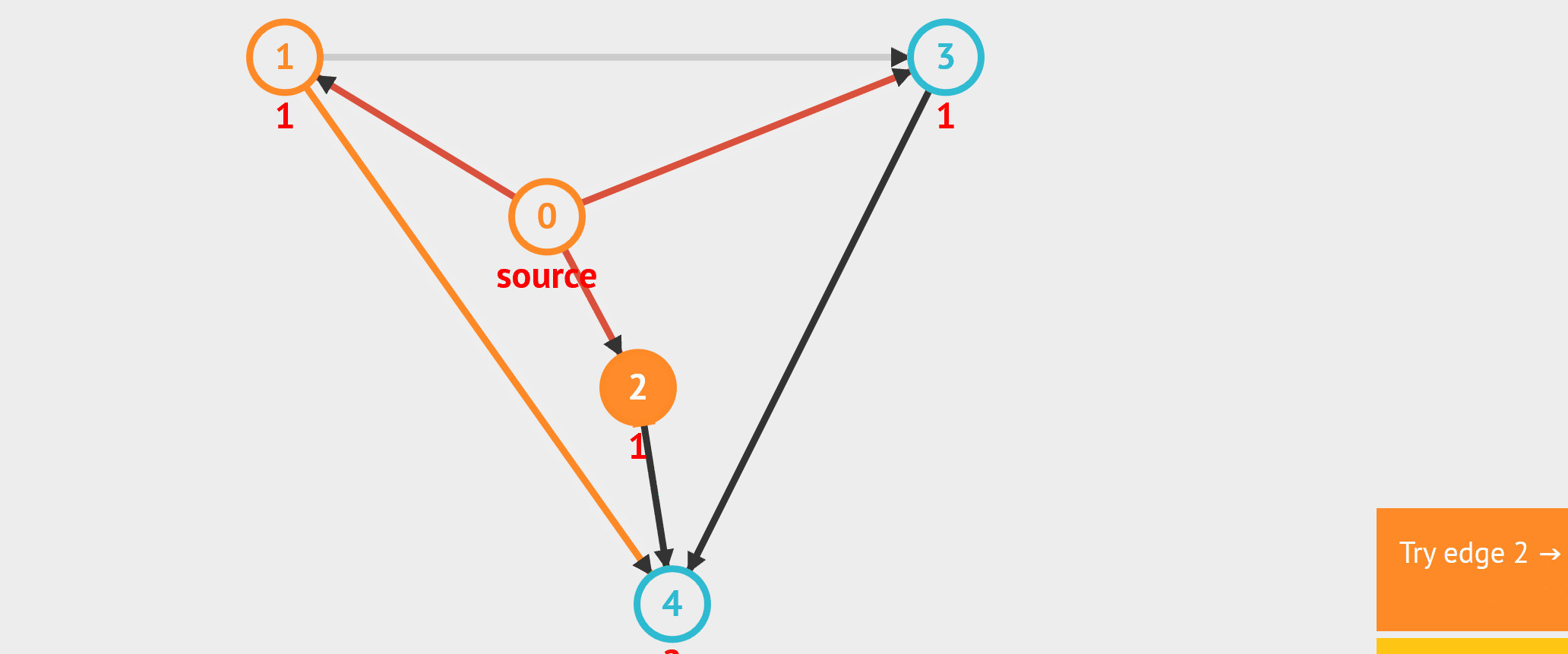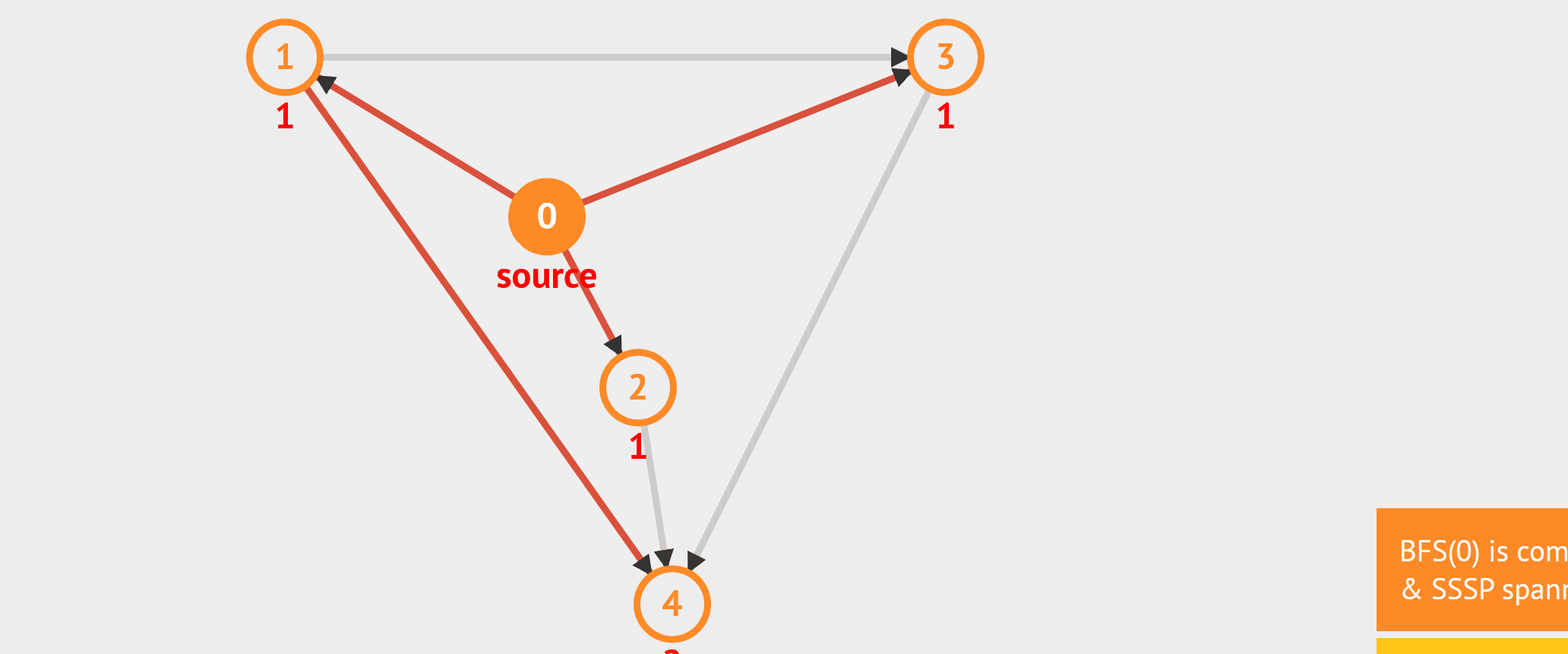

![](https://img2018.cnblogs.com/blog/1779545/201911/1779545-20191125220153196-1989860316.gif)
![](https://img2018.cnblogs.com/blog/1779545/201911/1779545-20191125220206265-194273465.gif)

//基于无向图邻接矩阵的广度遍历,非递归实现
public void BFSTraverse(int i){
list.add(vexs[i]);
BFS();
}
public void BFS(){
char temp=(char)list.poll();
int x=temp-'0';
isVisited[x]=1;
System.out.println(temp);
List nerborpointlist=getCurrent(x);
for(int i=0;i<nerborpointlist.size();i++){
char j=(char)nerborpointlist.get(i);
list.add(j);
int k=j-'0';
isVisited[k]=1;
}
if(!list.isEmpty()){
BFS();
}
}
public List getCurrent(int i){
List list1=new LinkedList();
for(int j=0;j<vexnum;j++){
if(matrix[i][j]==1&&isVisited[j]==0)
list1.add(vexs[j]);
}
return list1;
}

//基于无向图邻接矩阵的深度遍历,递归实现
public void DFSTraverse(int i){
DFS(this,i);
}
public void DFS(Graph a,int i){
isVisited[i]=1;
System.out.println(vexs[i]);
for(int j=0;j<vexnum;j++){
if(matrix[i][j]==1&&isVisited[j]==0){
DFS(a,j);
}
}
}
```

教材学习中的问题和解决过程

问题1：DFS的返回需要返回到起始访问点吗？
问题1解决方案：不需要。若是发现已经遍历到一条路径的终点了，就原路返回，若是返回的顶点处，有邻接点未被访问，相当于走进该邻接点所在的那条支路，再进行向前走的操作，若是走到头了，则原路返回，重新寻找支路，直到所有点都被遍历完为止。

代码调试中的问题和解决过程

问题1：关于根据顶点的名字获取顶点在顶点数组中的位置和边上的位置，每次使用遍历的方法去找太麻烦了，有没有简便的方案？
问题1解决方案：按照顶点的下标设置顶点的名字，比如V1在顶点数组（char[]）中存为‘1’，查找在数组中的下标时，直接使用char[i]-'0'即可

代码托管

结对及互评

点评过的同学博客和代码

本周结对学习情况
- 20182303

上周错题总结

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	10000行	30篇	400小时
第一周	246/246	2/2	30/30	初步掌握linux命令、java小程序和jdb调试
第二周	73/319	3/3	30/60
第三周	906/1225	3/6	20/80
第四周	748/1973	2/8	20/100
第五周	849/2822	2/10	20/120
第六周	962/ 3784	2/12	30/150
第七周	1883/5668	3/15	50/200
第八周	579/6247	1/16	30/230
第九周	1195/7442	3/19	30/260
第十周		1/20	40/300

参考链接

数据结构与算法学习笔记——图(Graph)

来源：https://www.cnblogs.com/lengchong/p/11930907.html

标签

char

邻接矩阵

算法与数据结构

数据结构