数据结构与算法
1. 概述
什么是计算机科学?
首先明确的一点就是计算机科学不仅仅是对计算机的研究,虽然计算机在科学发展的过程中发挥了重大的作用,但是它只是一个工具,一个没有灵魂的工具而已。所谓的计算机科学实际上是对问题、解决问题以及解决问题的过程中产生产生的解决方案的研究。例如给定一个问题,计算机科学家的目标是开发一个算法来处理该问题,最终得到该问题的解、或者最优解。所以说计算机科学也可以被认为是对算法的研究。因此我们也可以感受到,所谓的算法就是对问题进行处理且求解的一种实现思路或者思想。
什么是算法?
问题,解决问题,解决问题过程中产生的解决方案,算法就是对问题进行处理且求解的一种实现思路或者思想
评判程序优劣的方法?
时间复杂度:
评判规则: 量化算法执行的操作/执行步骤的数量
最重要的项: 时间复杂度表达式中最有意义的项
例如:
def sumOfN(n):
theSum = 0 # 1
for i in range(1, n + 1):
theSum = theSum + i # n
return theSum
print(sumOfN(10))
# 此算法的时间复杂度位O(n)
分析算法时间复杂度的步骤:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数。
- 得到的最后结果就是大O阶。
常见的时间复杂度:
O(1) < O(logn) < (n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
计算算法执行的平均耗时:
当一些算法各种调用其他算法,不好算,就用这个
timeit模块:该模块可以用来测试一段python代码的执行速度/时长。 Timer类:该类是timeit模块中专门用于测量python代码的执行速度/时长的。原型为:class timeit.Timer(stmt='pass',setup='pass')。 stmt参数:表示即将进行测试的代码块语句。 setup:运行代码块语句时所需要的设置。 timeit函数:timeit.Timer.timeit(number=100000),该函数返回代码块语句执行number次的平均耗时。
from timeit import Timer
# 使用timeit计算算法的平均耗时
def test01():
alist = []
for i in range(1000):
alist.append(i)
return alist
def test02():
alist = []
for i in range(1000):
alist.insert(0, i)
return alist
def test03():
alist = []
for i in range(1000):
alist = alist + [i]
return alist
def test04():
alist = list(range(1000))
return alist
if __name__ == '__main__':
# 第一个参数: 要执行的代码块
# 第二个参数: 执行代码块的配置
timer = Timer("test04()", "from __main__ import test04")
print(timer.timeit(1000))
# 参数: 执行次数
什么是数据结构?
对于数据的组织方式就被称作为数据结构.数据结构解决的就是一组数据如何进行保存,保存形式是怎样的问题 使用不同的形式组织数据,在基于查询时的时间复杂度是不一样的 因此认为算法是为了解决实际问题而设计的,数据结构是算法处理问题的载体
2. 数据结构
2.1栈
特性: 先进先出的数据结构
需要理解: 栈顶 栈尾
# 基于python列表模拟栈
class Stack:
def __init__(self):
self.items = []
def push(self, item):
"""添加元素"""
self.items.append(item)
def pop(self):
"""取出元素"""
return self.items.pop()
def peek(self):
"""查询当前栈顶元素的索引"""
return (self.size() - 1) if not self.isEmpty() else None
def size(self):
"""当前栈的元素个数"""
return len(self.items)
def isEmpty(self):
"""是否为空"""
return self.items == []
2.2 队列
特点: 先进先出
2.2.1 单端队列
class Queue:
def __init__(self):
self.items = []
def enqueue(self, item):
"""添加元素"""
self.items.append(item)
def dequeue(self):
"""取出元素"""
return self.items.pop(0) if not self.isEmpty() else None
def size(self):
"""队列元素个数"""
return len(self.items)
def isEmpty(self):
"""是否为空"""
return self.items == []
应用实例:
6个孩子围城一个圈,排列顺序孩子们自己指定。第一个孩子手里有一个烫手的山芋,需要在计时器计时1秒后将山芋传递给下一个孩子,依次类推。规则是,在计时器每计时7秒时,手里有山芋的孩子退出游戏。该游戏直到剩下一个孩子时结束,最后剩下的孩子获胜。请使用队列实现该游戏策略,排在第几个位置最终会获胜。
分析:
我们可以使用队列来模拟这个圆,因为计时7秒时,拿着山芋的孩子被淘汰,而队列只能从出口端取值,那么只需要让初始的山芋在队列第一个元素的孩子的手中,每次传递,让第一个孩子取出队列,然后再加到队列的尾部,那么下一个孩子就变成了队列的第一个元素,而山芋也在他的手中,然后每传递6此后,将队列的第一个孩子淘汰,直到队列里只有一个孩子
def func():
q = Queue()
# 准备6个孩子
for i in ['A', 'B', 'C', 'D', 'E', 'F']:
q.enqueue(i)
while q.size() > 1:
# 队列的长度等于1时退出循环
for i in range(6):
item = q.dequeue()
q.enqueue(item)
# 每传递6次,将第一个孩子淘汰
q.dequeue()
return q.dequeue()
print(func()) # E
两个队列实现一个栈:
# 栈: 先进先出
# 队列: 先进后出
class Stack:
def __init__(self):
self.q1 = Queue()
self.q2 = Queue()
def push(self, item):
"""添加元素"""
self.q1.enqueue(item)
if self.q1.size() > 1:
self.q2.enqueue(self.q1.dequeue())
def pop(self):
"""取出元素"""
if self.q1.size() > 0:
return self.q1.dequeue()
if self.q2.size() == 0:
return None
for i in range(self.q2.size() - 1):
self.q1.enqueue(self.q2.dequeue())
ret = self.q2.dequeue()
q1 = self.q1
q2 = self.q2
self.q1 = q2
self.q2 = q1
return ret
def size(self):
"""当前栈的元素个数"""
return self.q1.size() + self.q2.size()
def isEmpty(self):
"""当前栈是否为空"""
return self.size() == 0
def peek(self):
"""当前栈顶元素的索引"""
return (self.size() - 1) if not self.isEmpty() else None
2.2.2 双端队列
特点: 两端均可以添加,取出
class Deque:
def __init__(self):
self.items = []
def addFront(self, item):
self.items.insert(0, item)
def addRear(self, item):
self.items.append(item)
def removeFront(self):
if self.isEmpty():
return None
return self.items.pop(0)
def removerRear(self):
if self.isEmpty():
return None
return self.items.pop(-1)
def isEmpty(self):
return self.items == []
def size(self):
return len(self.items)
使用双端队列判断一个字符串是否回文:
def check(s):
dq = Deque()
for i in s:
dq.addFront(i)
while dq.size() > 1:
if dq.removeFront() != dq.removerRear():
return False
return True
2.3 顺序表
python的两种顺序表:


顺序表的弊端:顺序表的结构需要预先知道数据大小来申请连续的存储空间,而在进行扩充时又需要进行数据的搬迁(非尾部的插入,删除)。
2.4 链表
2.4.1 单链表
概念:
计算机的作用:
用来计算和存储二进制的数据
变量的概念:
python中变量就是引用,变量其实表示的就是计算机中的一块内存 严谨的来说,变量其实就是内存地址 一块内存空间会有两个默认的属性: 空间大小 内存地址 空间大小: bit bytes kb ... 内存地址: 方便计算机找到这块内存,进而拿到数据(寻址)
指向:
如果变量或者引用存储了模块内存空间地址后,则该变量或者引用指向该块内存
链表:相对于顺序表,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理且进行扩充时不需要进行数据搬迁。
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是不像顺序表一样连续存储数据,而是每一个结点(数据存储单元)里存放下一个结点的信息(即地址)
Python模拟单链表:
# 节点类
class Node:
def __init__(self, item):
self.item = item
self.next = None
# 链表
class SingleLink:
def __init__(self):
"""__head属性永远指向第一个结点,如果链表为空,则指向空"""
self.__head = None
def is_empty(self):
"""是否为空"""
return self.__head == None
def length(self):
"""链表长度"""
cur = self.__head
length = 0
while cur:
length += 1
cur = cur.next
return length
def add(self, item):
"""链表头部添加元素"""
node = Node(item)
node.next = self.__head
self.__head = node
def append(self, item):
"""链表尾部插入元素"""
node = Node(item)
cur = self.__head
if not cur:
self.__head = node
return
pre = None # 用来记录cur结点的上一个结点
while cur:
pre = cur
cur = cur.next
pre.next = node
def travel(self):
"""遍历链表"""
lst = []
cur = self.__head
while cur:
lst.append(cur.item)
# 每次循环都要改变cur
cur = cur.next
return lst
def insert(self, pos, item):
"""指定位置插入结点"""
if not 0 <= pos <= self.length() - 1:
return
if pos == 0:
self.add(item)
else:
node = Node(item)
cur = self.__head
pre = None
for i in range(pos):
pre = cur
cur = cur.next
node.next = cur
pre.next = node
def remove(self, item):
"""删除指定结点"""
cur = self.__head
pre = None
while cur:
if cur.item == item:
# 此时cur就是要删除的结点
if not pre:
# 此时删除的是第一个结点
self.__head = cur.next
else:
pre.next = cur.next
return
pre = cur
cur = cur.next
def search(self, item):
"""查找某个item是否存在于链表的结点中"""
find = False
cur = self.__head
while cur:
if cur.item == item:
find = True
break
cur = cur.next
return find
def clear(self):
"""清空链表"""
self.__head = None
def sort(self, lst):
"""
纯粹为了练习...
基于链表的排序方法,此方法单独使用,使用前确保链表是空的
:param lst: 乱序的数值
:return:
"""
for item in lst:
node = Node(item)
if self.is_empty():
self.__head = node
else:
cur = self.__head
pre = None
while cur and cur.item < item:
pre = cur
cur = cur.next
if not pre:
node.next = cur
self.__head = node
else:
node.next = cur
pre.next = node
return self.travel()
实现链表的翻转:
思路一:
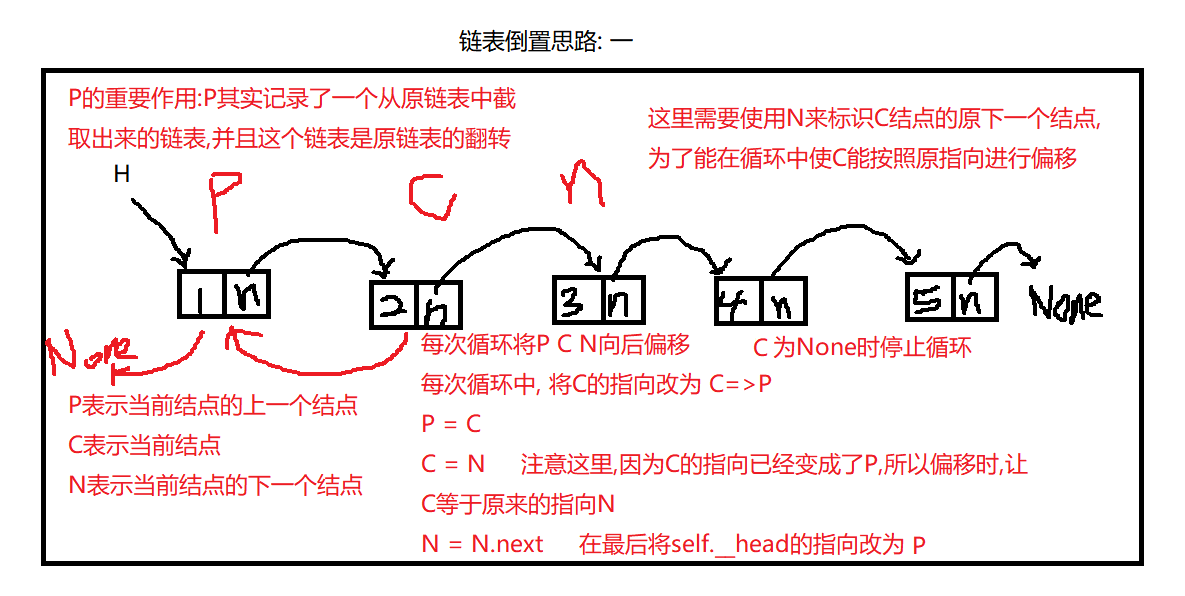
def reverse(self):
"""
翻转链表的第一种思路:依次改变结点的指向,将结点指向此结点的上一个结点,并使用pre来指向这个节点,相当于将原链表打断成了2条,在循环中依次从原链表加到新链表的头部,完成倒置
为了保证在循环时能找到此结点的下一个结点,使用变量nex引用结点的原指向
"""
if self.is_empty():
return None
# 当前节点
cur = self.__head
# 当前节点的上一个节点
pre = None
# 当前节点的下一个节点
nex = cur.next
while cur:
# 当前节点存在
cur.next = pre # 将当前节点的指向变为上一个节点
# 进行偏移
pre = cur # 这里注意,其实pre已经指向一个反向的链表
# 这里使用nex而不是cur.next,是因为cur.next已发生改变
cur = nex
if cur:
# 如果cur为None,则已遍历完毕原链表,跳出循环
nex = nex.next
self.__head = pre
return self.travel()
思路二:

def reverse(self):
if self.is_empty():
return
# 1.将链表用一个新的头部指向
new_head = self.__head
self.__head = None
# 2.遍历新的链表,依次将每个节点插入原链表的头部
while new_head:
# 注意:这里需要先赋值给cur,保证当前结点不会丢失
cur = new_head
# 将当前结点从new_head中删除
new_head = new_head.next
# 将当前结点插入__head的头部
cur.next = self.__head
self.__head = cur
return self.travel()
2.5 二叉树
二叉树和链表的区别是二叉树的每个结点有左右两个指向
二叉树:
普通二叉树
排序二叉树
根节点
左右叶子节点
子树:完整的子树和非完整的子树
每一颗子树根节点可以作为另一颗子树的左右叶子节点
每一个节点其实都可以作为一颗子树的根节点
2.5.1 普通二叉树
class Node:
"""结点类"""
def __init__(self, item):
self.item = item
# 左右两个指向
self.left = None
self.right = None
class Tree:
"""二叉树类"""
def __init__(self):
# 和链表一样,二叉树中只保存最上面的根节点
self.root = None
def insert(self, item):
"""插入结点"""
node = Node(item)
if not self.root:
self.root = node
return
# 如果二叉树不为空
cur = self.root
# 这里需要使用一个队列,用来保存每颗子树的根节点
queue = []
while True:
if not cur.left:
cur.left = node
break
else:
queue.append(cur.left)
if not cur.right:
cur.right = node
break
else:
queue.append(cur.right)
cur = queue.pop(0)
def travel(self):
"""遍历二叉树: 广度遍历"""
# 这里需要使用一个队列,用来保存每颗子树的根节点
if not self.root:
return
cur = self.root
queue = [cur]
while queue:
cur = queue.pop(0)
print(cur.item)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
def search(self, item):
"""查找某个结点是否存在"""
if not self.root:
return False
cur = self.root
queue = [cur]
while queue:
cur = queue.pop(0)
if cur.item == item:
return True
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
return False
2.5.2 排序二叉树
二叉树的遍历
广度遍历:横向
深度遍历:纵向。一定是作用在每一颗子树中的
前序遍历: 根左右
中序遍历:左根右
后序遍历:左右根
准则:当向排序二叉树中插入节点的时候,让节点和树的根节点进行大小比较。比根节点大的节点需要插入到树的右侧,否则插入到树的左侧。
中序遍历结合有序二叉树,即可实现有序输出

class Node:
"""结点类"""
def __init__(self, item):
self.item = item
# 左右两个指向
self.left = None
self.right = None
class SortTree:
def __init__(self):
self.root = None
def insert(self, item):
node = Node(item)
if not self.root:
self.root = node
return
cur = self.root
while True:
if cur.item > item:
if not cur.left:
cur.left = node
return
cur = cur.left
else:
if not cur.right:
cur.right = node
return
cur = cur.right
def travel(self):
"""遍历二叉树: 广度遍历"""
# 这里需要使用一个队列,用来保存每颗子树的根节点
if not self.root:
return
cur = self.root
queue = [cur]
while queue:
cur = queue.pop(0)
print(cur.item)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
def forward(self, cur=1):
"""前序遍历: 根左右 注意要作用到每一个子树中"""
if not self.root:
return
if not cur:
return
if cur == 1:
cur = self.root
print(cur.item)
self.forward(cur.left)
self.forward(cur.right)
def middle(self, cur=1):
"""中序遍历: 左根右"""
if not self.root:
return
if not cur:
return
if cur == 1:
cur = self.root
self.middle(cur.left)
print(cur.item)
self.middle(cur.right)
def back(self, cur=1):
"""后序遍历: 左右根"""
if not self.root:
return
if not cur:
return
if cur == 1:
cur = self.root
self.back(cur.left)
self.back(cur.right)
print(cur.item)
3. 算法
3.1 查找算法
3.1.1 顺序查找
当数据存储在诸如列表的集合中时,我们说这些数据具有线性或顺序关系。 每个数据元素都存储在相对于其他数据元素的位置。 由于这些索引值是有序的,我们可以按顺序访问它们。 这个过程产实现的搜索即为顺序查找。
时间复杂度: O(n)
lst = [1, 3, 5, 7, 11, 22, 111]
def search(alist, item):
"""顺序查找"""
for i in alist:
if i == item:
return True
return False
print(lst, 1) # True
3.1.2 二分查找
注意: 二分查找只能作用于有序列表
有序列表对于我们的实现搜索是很有用的。在顺序查找中,当我们与第一个元素进行比较时,如果第一个元素不是我们要查找的,则最多还有 n-1 个元素需要进行比较。 二分查找则是从中间元素开始,而不是按顺序查找列表。 如果该元素是我们正在寻找的元素,我们就完成了查找。 如果它不是,我们可以使用列表的有序性质来消除剩余元素的一半。如果我们正在查找的元素大于中间元素,就可以消除中间元素以及比中间元素小的一半元素。如果该元素在列表中,肯定在大的那半部分。然后我们可以用大的半部分重复该过程,继续从中间元素开始,将其与我们正在寻找的内容进行比较。
时间复杂度: O(logN)
def search(alist, item):
"""二分查找的循环实现"""
start_index = 0
end_index = len(alist) - 1
while start_index <= end_index:
# 当start_index > end_index时,跳出循环
# 需要注意的是start_index == end_index时,此时需要比较这最后一个值
# 而且大多数情况下,start_index == end_index才是我们查找的值
middle_index = (start_index + end_index) // 2
if alist[middle_index] == item:
# 找到了
return True
elif alist[middle_index] < item:
# 中间值比查找值小,说明查找值在右侧
start_index = middle_index + 1
else:
# 中间值比查找值大,说明查找值在左侧
end_index = middle_index - 1
# 如果循环结束仍然没有return True,说明不存在查找值
return False
def search(alist, item):
"""二分查找的递归实现"""
if not alist:
# 递归出口
# 当剩余的区间为0时,说明没有查找值
return False
middle_index = (len(alist) - 1) // 2
if alist[middle_index] == item:
# 找到了
return True
elif alist[middle_index] < item:
# 中间值比查找值小,说明查找值在右侧
return search(alist[middle_index + 1:], item)
else:
# 中间值比查找值大,说明查找值在左侧
# 这里需要注意一下: 切片顾头不顾尾
return search(alist[:middle_index], item)
3.2 排序算法
3.2.1 冒泡排序
时间复杂度: O(n^2)
def sort(alist):
"""冒泡排序"""
# 第二步: 通过循环内存循环,依次将最大值移动到最后
# 每次循环只需要比较已确定位置元素的前面的元素即可
for j in range(len(alist) - 1):
for i in range(len(alist) - 1 - j):
# 第一步: 将每一个元素和它后面的元素比较
# 如果它比它的后一个元素大,将它与它后面的元素交换位置
# 这样循环结束时,最大值就被移动到了最后
if alist[i] > alist[i + 1]:
alist[i], alist[i + 1] = alist[i + 1], alist[i]
return alist
3.2.2 选择排序
时间复杂度: O(n^2)
但是元素交换次数比冒泡少了一点,所以比冒泡快了一丢丢
def sort(alist):
"""选择排序"""
for j in range(len(alist) - 1):
max_num_index = 0 # 假定一个最大值的索引
for i in range(len(alist) - 1 - j):
# 每次循环判断每一个值如果比最大值索引对应的值大,则更改最大值对应的索引
# 即每次循环找出了此次循环的最大值所对应的索引
# 又因为max_num_index默认为0,所以不需要和索引0的值进行比较
if alist[i + 1] > alist[max_num_index]:
max_num_index = i + 1
# 在循环结束后,将最大值索引所对应的值和此次循环的最后一个值进行交换
alist[max_num_index], alist[len(alist) - 1 - j] = alist[len(alist) - 1 - j], alist[max_num_index]
return alist
3.2.3 插入排序
时间复杂度: O(n^2)
思路:
将乱序的序列假设分成两部分
有序集合
无序集合
将无序集合的每一个元素依次有序的插入到有序集合中
def sort(alist):
"""插入排序"""
for i in range(1, len(alist)):
# i: 表示此时有序集合中有i个值(初始为1),最多有len(alist)个值
# 所以i也可以表示无序集合的第一个元素的索引
while i:
if alist[i] < alist[i - 1]:
# 判断无序集合的第一个元素和有序集合的最后一个值的大小
# 如果它比有序集合的最后一个值小,则将它俩交换位置
alist[i], alist[i - 1] = alist[i - 1], alist[i]
i = i - 1
else:
break
# 如果有序集合有多个值
# 则需要将无序集合的第一个元素和他们依次进行比较,直到它前面的值它小
# 当i为0时,它的前面没有值了,说明它是最小的,退出循环
return alist
3.2.4 希尔排序
希尔排序:插入排序的改进版
增量:
初始值:元素个数整除2
增量值表示的分组的组数
首先它把较大的数据集合分割成若干个小组(逻辑上分组),然后对每一个小组分别进行插入排序,此时,插入排序所作用的数据量比较小(每一个小组),插入的效率比较高 , 同组元素的索引差称为增量
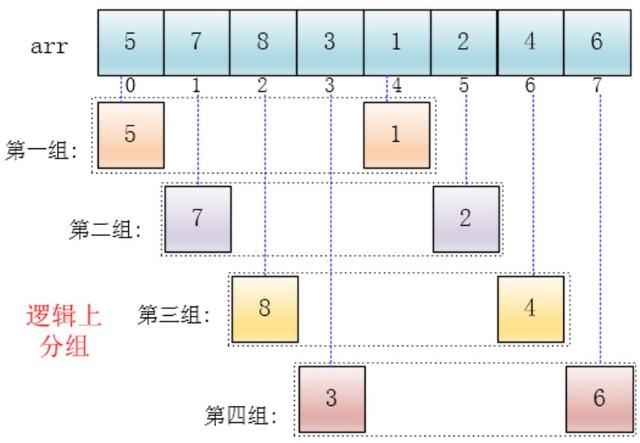
每次循环结束,数据集合都变得更有序了一些(不是完全有序),然后将增量变为当前增量的一半,再次进行循环,直到增量为1时,完成排序

def sort(alist):
"""希尔排序"""
# 声明一个变量gap表示增量: 即分组的间距,初始值为列表长度//2
gap = len(alist) // 2
while gap >= 1:
for i in range(len(alist) - gap):
# alist[i],alist[i + gap]每组的相邻(增量)的元素,进行比较
# 如果前面的比后面的大,则交换位置
while i >= 0:
if alist[i] > alist[i + gap]:
alist[i], alist[i + gap] = alist[i + gap], alist[i]
i = i - gap
else:
break
gap = gap // 2
return alist
3.2.5 快速排序
快排的核心思想是分而治之,指定一个基准值,将无序序列分为比基准值小和比基准值大,两部分,然后对这两部分在进行基准值分化,直到每部分只有一个值,则完成排序
难点在于如果将无序序列分为小于基准值和大于基准值两部分
思路:
将列表中第一个元素设定为基准数字,赋值给mid变量,然后将整个列表中比基准小的数值放在基准的左侧,比基准到的数字放在基准右侧。然后将基准数字左右两侧的序列在根据此方法进行排放。 定义两个指针,low指向最左侧,high指向最右侧 然后对最右侧指针进行向左移动,移动法则是,如果指针指向的数值比基准小,则将指针指向的数字移动到基准数字原始的位置,否则继续移动指针。 如果最右侧指针指向的数值移动到基准位置时,开始移动最左侧指针,将其向右移动,如果该指针指向的数值大于基准则将该数值移动到最右侧指针指向的位置,然后停止移动。 如果左右侧指针重复则,将基准放入左右指针重复的位置,则基准左侧为比其小的数值,右侧为比其大的数值。
def sort(alist, start=0, end=None):
"""
快排的参数版
思路: 我们都知道快排采用了分治思想
难点在于如何将一个无序序列分为小于一个值和大于一个值的两部分
"""
low = start
high = end
if high is None:
# 第一次 high 为None
high = len(alist) - 1 # 无序序列的最后一个位置
if high < 1:
# 如果high < 1 说明初始序列只有一个值,或为空,直接返回
return alist
if low >= high:
# 递归出口
return
mid = alist[low] # 基准值,通常使用无序序列的第一个元素的值
while low < high:
# 这里完成了将无序序列分为小于基准值和大于基准值两部分
while low < high:
if alist[high] < mid:
alist[low] = alist[high]
low = low + 1
break
high = high - 1
while low < high:
if alist[low] > mid:
alist[high] = alist[low]
high = high - 1
break
low = low + 1
alist[low] = mid
sort(alist, start=start, end=low - 1)
sort(alist, start=low + 1, end=end)
return alist
def sort(alist):
if len(alist) < 2:
return alist
low = 0
high = len(alist) - 1
mid = alist[0]
while low < high:
while low < high:
if alist[high] < mid:
alist[low] = alist[high]
break
high = high - 1
while low < high:
if mid < alist[low]:
alist[high] = alist[low]
break
low = low + 1
return sort(alist[0:low]) + [mid] + sort(alist[low + 1:])