1. 技术文章
  2. 进化版数据结构（可持久化）

进化版数据结构（可持久化）

由 牧云@^-^@ 提交于 2019-11-26 20:34:58

·线段树

主席树和可持久化线段树有什么区别？

这里写图片描述
这里写图片描述
主席树（可持久化线段树）

可持久化线段树（Persistent data structure）最主要的功能就是可以查询历史版本。那么presistent≈president（主席），得名主席树。

给你个问题：

给你一段数列，要求查询一段区间的第k小数。\((n<=10^5)\)

要怎么做？【面面相觑】

很容易想到两种方法：
①建一棵线段树，然后再每个表示区间的节点上都建一棵权值线段树！直接查询即可。
②建n棵线段树，第i棵线段树表示1~i里面所有的数构成的权值线段树！那么查询区间的时候就直接像使用前缀和一样，每个节点表示的权值区间在这个查询的区间中拥有数的个数就是：当前节点个数减去区间左端点建的树中对应的点的数量。
例如：
这里写图片描述
我们查询区间[2~4]的第k小，我们可以很显然的地得出：每个节点的值其实就是在第4棵线段树上这个节点的值减去在第一棵线段树上这个节点的值。然后按照权值线段树的查询规律下去找就好了。
很明显这个算法的时间空间复杂度都是\(O(n^2\) \(log\) \(n)\)的。

主席树的主体是线段树，准确的说，是很多棵线段树。那么如何既能建出那么多棵线段树，同时不会MLE、TLE.

很显然我们会发现，修改前缀和的时候只有可能加入一个数，而受到这个数影响的只有可能有一条链，那么其他我们新开的点就都是废的了。我们每次只需要新建这条链，把其他跟上次一样的东西继承过来就好了，被继承的点就叫做共用！当然一个点有可能会被多个点共用！这样的话我们就可以将空间和时间复杂度大大减小。
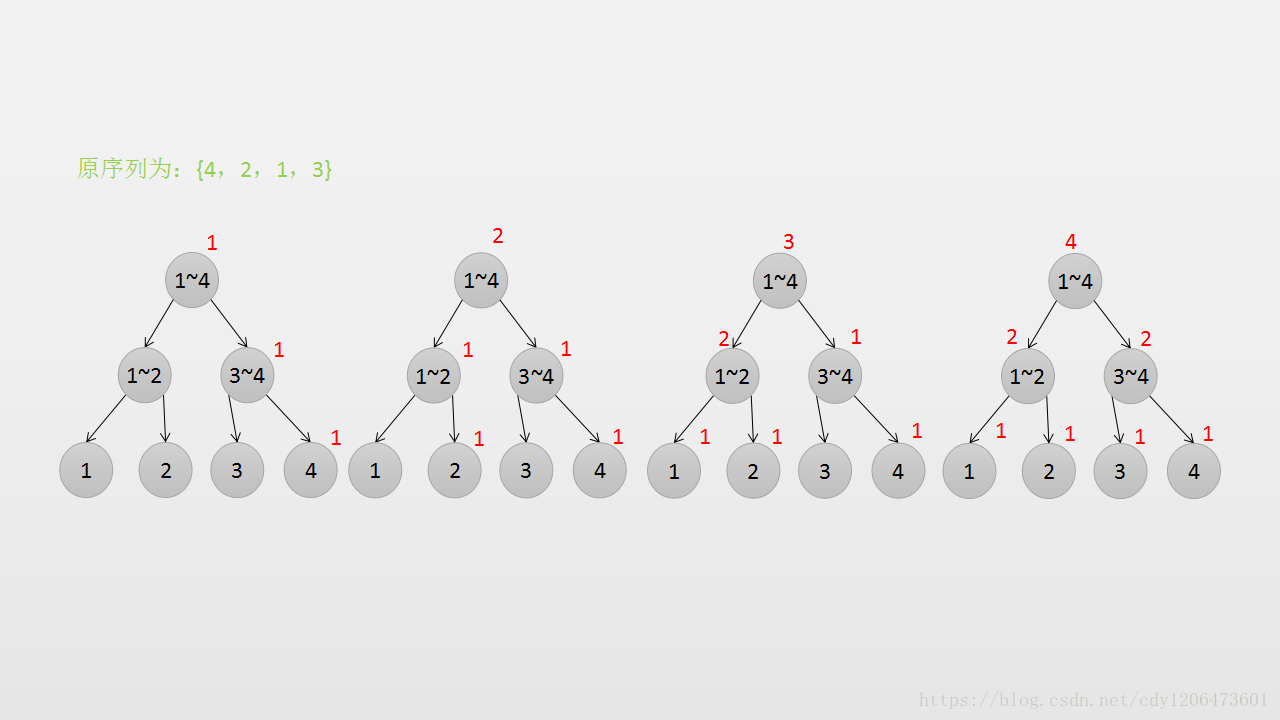
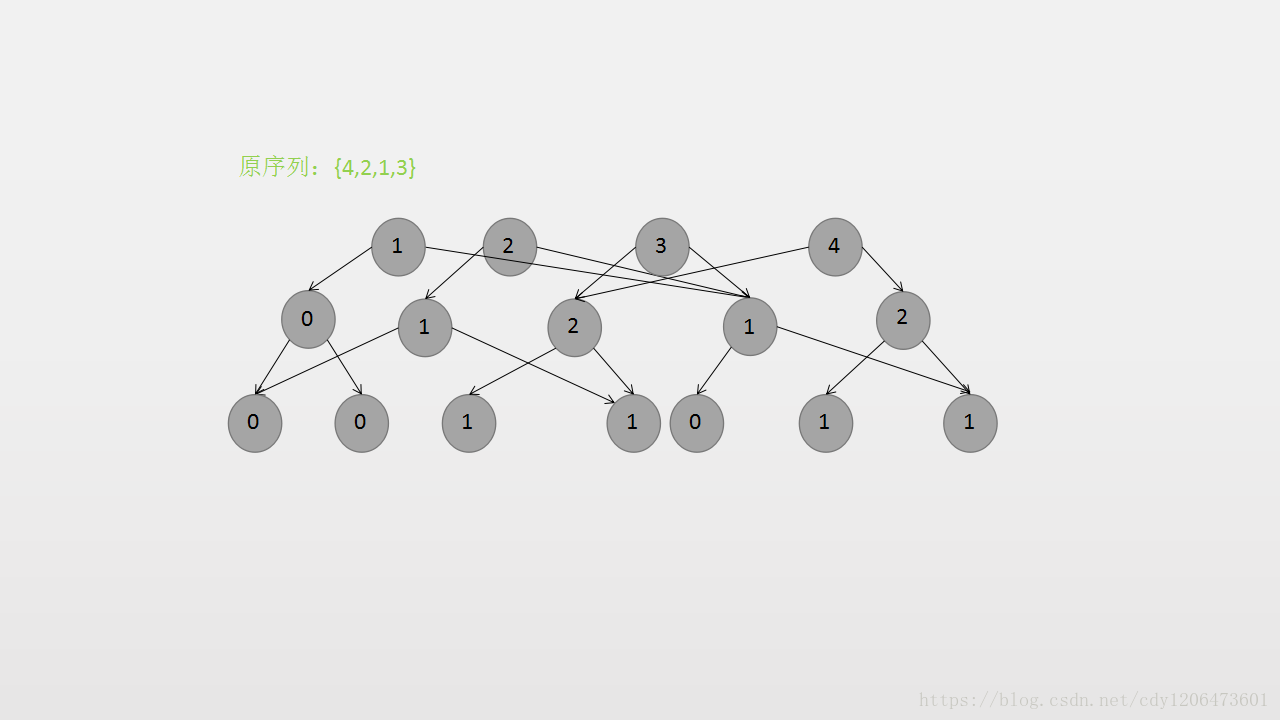
图如下：
这里写图片描述
对照上图，节点内的数字表示以该点为根的字数拥有的数字个数。这样空间省去很多，每次只会增加一条链，那么空间复杂度就是\(O(n log n+n log n)\),时间复杂度和普通线段树一样，都是每次操作只有\(O(log n)\)的时间。

Code：

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
struct Moon{
    int rs,ls,num;
}tree[4000010];
struct Candy{
    int x,y;
}a[200010],b[200010];
int root[200010],c[200010];
int n,m,sz,N;
bool cmp(Candy a,Candy b){return a.x<b.x||a.x==b.x&&a.y<b.y;}
void add(int l,int r,int u,int v,int x)
{
    if(l==r)
    {
        ++tree[v].num;
        return;
    }
    int mid=(l+r)/2;
    if(x<=mid)
    {
        tree[v].rs=tree[u].rs;
        tree[v].ls=++sz;
        add(l,mid,tree[u].ls,tree[v].ls,x);
    }
    else
    {
        tree[v].ls=tree[u].ls;
        tree[v].rs=++sz;
        add(mid+1,r,tree[u].rs,tree[v].rs,x);   
    }
    tree[v].num=tree[tree[v].ls].num+tree[tree[v].rs].num;
}
int query(int l,int r,int u,int v,int x)
{
    if(l==r) return l;
    int mid=(l+r)/2;
    if(x<=tree[tree[v].ls].num-tree[tree[u].ls].num) return query(l,mid,tree[u].ls,tree[v].ls,x);
    else return query(mid+1,r,tree[u].rs,tree[v].rs,x-(tree[tree[v].ls].num-tree[tree[u].ls].num));
}
int main()
{
    scanf("%d%d",&n,&m);
    int i,j,x,y,k,p;
    for (i=1;i<=n;++i) scanf("%d",&a[i].x),b[i].x=a[i].x,b[i].y=i;
    sort(b+1,b+1+n,cmp);
    for (i=1;i<=n;++i) a[b[i].y].y=i,c[i]=a[b[i].y].x;
    for (i=1;i<=n;++i) root[i]=++sz,add(1,n,root[i-1],sz,a[i].y);
    while(m--)
    {
        scanf("%d%d%d",&x,&y,&k);
        printf("%d\n",c[query(1,n,root[x-1],root[y],k)]);
    }
}

·带修主席树

  • 上述的主席树是一种优秀的处理历史版本以及区间第k值得做法，但是现在我们遇到了一个棘手的问题，如果上述问题中，我们需要修改某一个值，并且同时在线询问该怎么做呢?
  • 我们发现，如果按照上述做法做，修改的时间将会是\(O(n\) \(log\) \(n)\),因为我们对于修改位置以后每一棵树都要用log n 的时间去维护在这一位置上的值，显然这样的复杂度是不可接受的。
  • 我们可以想到使用树状数组去优化这种算法。
  • 我们发现树状数组的本质和主席树的本质是一样的，都是前缀和，那我们能不能把它们两个合并起来呢？

  • 答案是可以的，对于一颗树状数组上的每一个树节点x，我们都建一颗线段树，用来维护区间\([x-lowbit(x)+1..x]\)的所有信息，这样我们在修改的时候就遵循树状数组的修改原则修改。

    例题

    ZOJ2112 Dynamic Rankings
    给定一个数列，包括两个操作：
    Q i j k 询问区间[i..j]的第k小
    C i t 将第i个数改成t
    n<=50000,q<=10000
    带修主席树裸题。

    Code

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define maxn 50010
#define maxm 10010
#define maxN maxn+maxm
using namespace std;
struct Moon{
    int vol,ls,rs;
}tr[maxn];
int T,n,m,N,sz;
int a[maxn],dat[maxN],q1[maxn];
int root[maxn],kind[maxm],q2[maxn];
int qi[maxm],qj[maxm],qk[maxm],qt[maxm];
int lowbit(int x)
{
    return x&-x;
}
void clear()
{
    memset(tr,0,sizeof(tr));
    memset(root,0,sizeof(root));
}
int find(int x)
{
    int l,r,mid;
    for (l=1,r=N,mid=(l+r)/2;l<r;mid=(l+r)/2)
        if(dat[mid]<x) l=mid+1;else r=mid;
    return l;
}
void Modify(int &v,int l,int r,int x,int volue)
{
    if(!v) v=++sz;
    tr[v].vol+=volue;
    if(l==r) return;
    int mid=(l+r)/2;
    (x<=mid)?Modify(tr[v].ls,l,mid,x,volue):Modify(tr[v].rs,mid+1,r,x,volue);
}
void modify(int xx,int y,int c)
{
    for (;xx<=N;xx+=lowbit(xx)) Modify(root[xx],1,N,y,c);
}
int count()
{
    int sum=0;
    for (int i=1;i<=q1[0];++i) sum+=tr[tr[q1[i]].ls].vol;
    for (int i=1;i<=q2[0];++i) sum-=tr[tr[q2[i]].ls].vol;
    return sum;
}
int query(int ql,int qr,int k)
{
    memset(q1,0,sizeof(q1));
    memset(q2,0,sizeof(q2));
    int l=1,r=N,mid,Count,i;
    for (i=qr;i;i-=lowbit(i)) q1[++q1[0]]=root[i];
    for (i=ql-1;i;i-=lowbit(i)) q2[++q2[0]]=root[i];
    while(l<r)
    {
        Count=count(),mid=(l+r)/2;
        if(k<=Count)
        {
            for (i=1;i<=q1[0];++i) q1[i]=tr[q1[i]].ls;
            for (i=1;i<=q2[0];++i) q2[i]=tr[q2[i]].ls;
            r=mid;
        }
        else
        {
            for (i=1;i<=q1[0];++i) q1[i]=tr[q1[i]].rs;
            for (i=1;i<=q2[0];++i) q2[i]=tr[q2[i]].rs;
            l=mid+1,k-=Count;   
        }
    }
    return l;
}
int main()
{
    int i,j,k;char ch;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m),N=n;
        for (i=1;i<=n;++i) scanf("%d",&a[i]),dat[i]=a[i];
        for (i=1;i<=m;++i)
        {
            ch=getchar();while(ch!='Q'&&ch!='C') ch=getchar();
            if(ch=='Q') kind[i]=0,scanf("%d%d%d",&qi[i],&qj[i],&qk[i]);
            else kind[i]=1,scanf("%d%d",&qi[i],&qt[i]),dat[++N]=qt[i];
        } 
        sort(dat+1,dat+1+N),k=N,N=0;
        for (i=1;i<=k;++i) if(dat[i-1]!=dat[i]) dat[++N]=dat[i];
        for (i=1;i<=n;++i) modify(i,find(a[i]),1);
        for (i=1;i<=m;++i)
        {
            if(!kind[i]) printf("%d\n",dat[query(qi[i],qj[i],qk[i])]);
            else modify(qi[i],find(a[qt[i]]),-1),a[qi[i]]=qt[i],modify(qi[i],find(a[qi[i]]),1); 
        }clear();
    }
}

·Trie

可持久化trie和主席树十分类似

区别：主席树的主体是线段树，而可持久化trie的主体是trie，主导思想都是前缀和以及共用点。
如果你学完了主席树，那么可持久化trie也很容易理解了。 可持久化trie就是对于每个字符串S，我们都花\(O(|S|)\)的时间新建一棵有\(|S|\)个点的trie，将前面点的信息复制到当前点，并且不断新建点。

例题：【THUSC2015】异或问题

Description

给定长度为n的数列X={x1,x2,...,xn}和长度为m的数列Y={y1,y2,...,ym}，令矩阵A中第i行第j列的值Aij=xi xor yj，每次询问给定矩形区域i∈[u,d],j∈[l,r]，找出第k大的Aij。

Input

第一行包含两个正整数n,m，分别表示两个数列的长度第二行包含n个非负整数xi；
第三行包含m个非负整数yj；
第四行包含一个正整数p，表示询问次数；
随后p行，每行均包含5个正整数，用来描述一次询问，每行包含五个正整数u,d,l,r,k，含义如题意所述。

Output

共p行，每行包含一个非负整数，表示此次询问的答案。

Sample Input

3 3
1 2 4
7 6 5
3
1 2 1 2 2
1 2 1 3 4
2 3 2 3 4

Sample Output

6
5
1

Data Constraint

对于100%的数据，0<=Xi,Yj<2^31,
1<=u<=d<=n<=1000,
1<=l<=r<=m<=300000,
1<=k<=(d-u+1)*(r-l+1),
1<=p<=500
其中，部分测试数据有如下特征（互不包含）：
对于5%的数据，满足1<=m<=1000, 1<=p<=10, k=1;
对于15%的数据，满足1<=m<=3000, 1<=p<=200;
对于20%的数据，满足p=1;
对于30%的数据，满足k=1;
对于其余30%的数据，没有其他特征。

Code：

#include<cstdio>
#include<iostream>
#define maxn 1010
#define maxm 300010
using namespace std;
struct Moon{
    int son[2],sz;
}point[40*maxm];
struct Candy{
    int x,y;
}b[maxn];
int n,m,q,u,d,l,r,k,Q,sz;
int x[maxn],y[maxm],Root[maxm],len[maxm]; 
void add(int u,int v,int x,int p)
{
    point[v].sz=point[u].sz+1;
    if(p<0) return;
    int y=(x>>p)&1;
    point[v].son[y]=++sz;
    point[v].son[!y]=point[u].son[!y];
    add(point[u].son[y],point[v].son[y],x,p-1);
}
int query(int k,int p)
{
    if(p<0) return 0;
    int sum=0,y;
    for (int i=u;i<=d;++i)
    {
        y=(x[i]>>p)&1;
        sum+=point[point[b[i].y].son[!y]].sz-point[point[b[i].x].son[!y]].sz;
    }
    if(sum>=k)
    {
        for (int i=u;i<=d;++i) 
        {
            y=(x[i]>>p)&1;
            b[i].y=point[b[i].y].son[!y];
            b[i].x=point[b[i].x].son[!y];
        }
        return query(k,p-1)+(1<<p);
    }else
    {
        for (int i=u;i<=d;++i) 
        {
            y=(x[i]>>p)&1;
            b[i].y=point[b[i].y].son[y];
            b[i].x=point[b[i].x].son[y];
        }
        return query(k-sum,p-1);    
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    int i,j,p;
    for (i=1;i<=n;++i) scanf("%d",&x[i]);
    for (i=1;i<=m;++i) 
    {
        scanf("%d",&y[i]);
        for (p=y[i];p;p/=2) ++len[i];
        Q=max(Q,len[i]);
    }Q--;
    for (i=1;i<=m;++i) Root[i]=++sz,add(Root[i-1],Root[i],y[i],Q);
    scanf("%d",&q);
    while(q--)
    {
        scanf("%d%d%d%d%d",&u,&d,&l,&r,&k);
        for (i=u;i<=d;++i) b[i].x=Root[l-1],b[i].y=Root[r];
        printf("%d\n",query(k,Q));
    }
}
标签
线段树
主席树
数据结构
持久化
scanf
易学教程内所有资源均来自网络或用户发布的内容，如有违反法律规定的内容欢迎反馈！
该文章没有解决你所遇到的问题?点击提问,说说你的问题,让更多的人一起探讨吧!