最小生成树
接下来是介绍最小生成树的内容。
什么是最小生成树?
定义: 各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树( Minimum Cost Spanning Tree ),简称最小生成树。
构成最小生成树的算法有很多,其中多数的算法都是利用了最下生成树的一种性质:
性质: 假设N=(V,E)是一个连通网,U是顶点集V的一个非空子集。若(u,v)是一条具有最小权值(或者说代价)的边,其中u∈U,v∈V-U,那么必定存在一颗包含边(u,v)的最小生成树
总结起来,得具备这些条件:
- 是一个连通网(连通图)
- 各边有权值
如果还不了解,那么我们来举一个例子:
比方说我们需要在n个城市中建立一个联系网,因为城市众多,我们当然不可能一一给他们都连通,考虑到价格问题,我们必须得用最小的代价从而连通所有的城市。
该怎么做呢?好难(っ °Д °;)っ
我们用圆圈来表示每个城市
然后用箭头中包含的值来表示权值
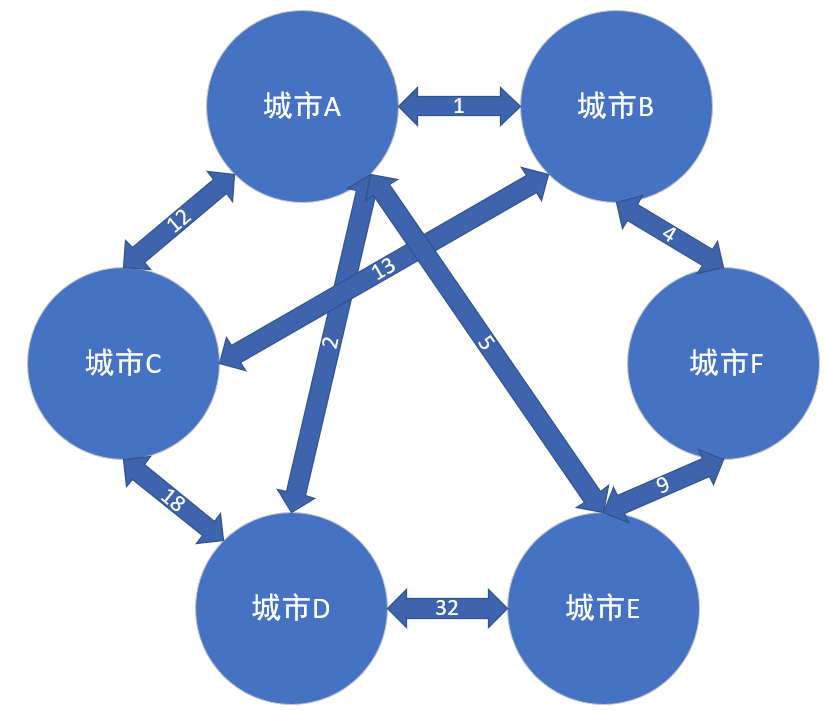
我们的问题来了,我们该怎样去选择,从而达到我们的目的呢? ( 我们的目的是:德玛西亚d=====( ̄▽ ̄*)b.......当然....目的是选择几条路线,组成的权值最小,并且能够把这几个点连接上...... )
首先我们用眼睛观察.....然后我们很容易选出这几条路线:
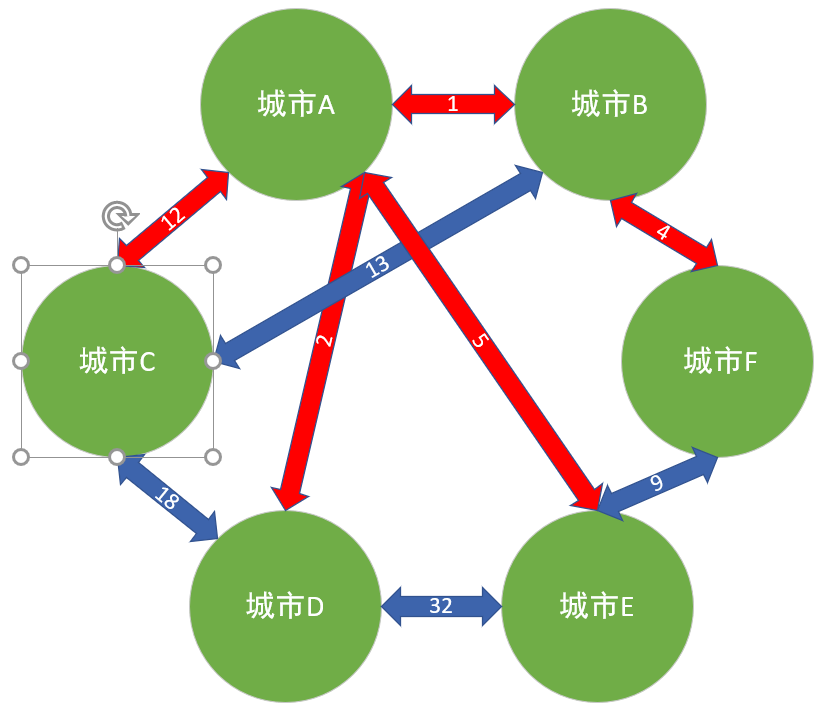
然后我们来算算,总权值是:1+2+4+5+12=24。没错,这就是最小生成树的构成,我们所选的路线并没有错。那么问题来了。我们是 怎么选 的呢?
还记得我们刚刚选的方式么?我的思路是,先把他们的各个边按照权值从小到大排序,排完序之后,再从中选出我所需要的边,直到所有的点覆盖完成,当然,如果有一条边是存在于已经连过的两个顶点之间,我就不要了,因为这两个城市已经走过了(●ˇ∀ˇ●)。
当所有的顶点都连接完成之后,我们的最小生成树也就构成了。如果排完序那么我们是这样的一个序列:
| 城市 | 可通城市 | 权值 |
|---|---|---|
| A | B | 1 |
| A | D | 2 |
| B | F | 4 |
| A | E | 5 |
| E | F | 9 |
| A | C | 12 |
| B | C | 13 |
| C | D | 18 |
| D | E | 32 |
然后对应 A B C D E F 转换为数字便是: 1 2 3 4 5 6
然后,我们从小到大,选择便是以下的情况: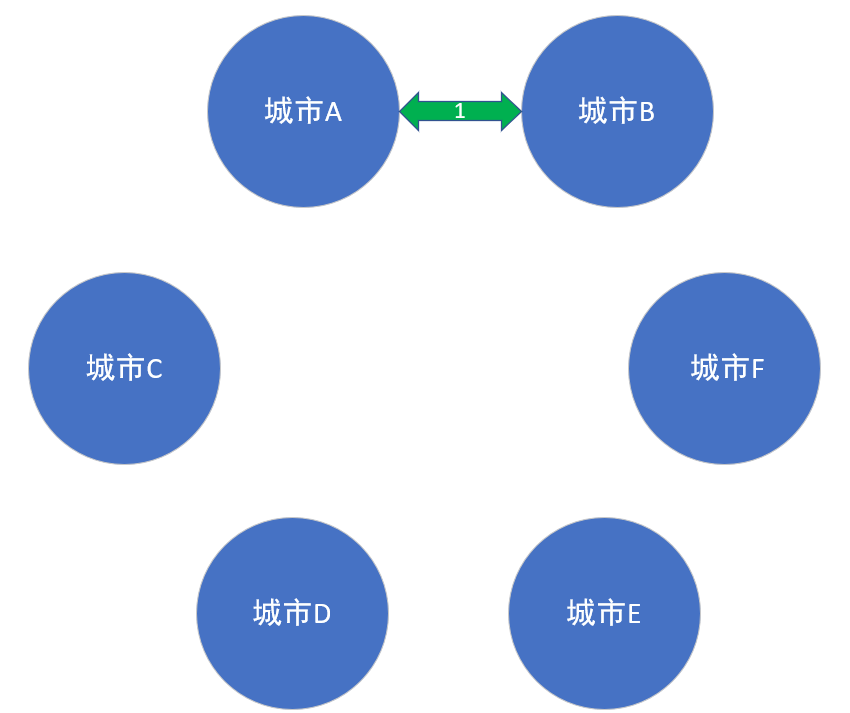
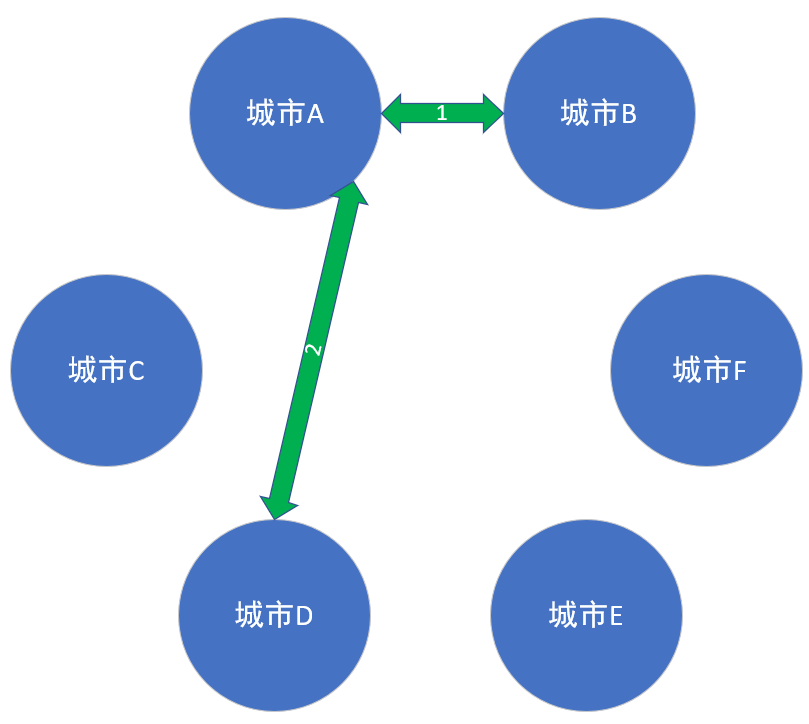
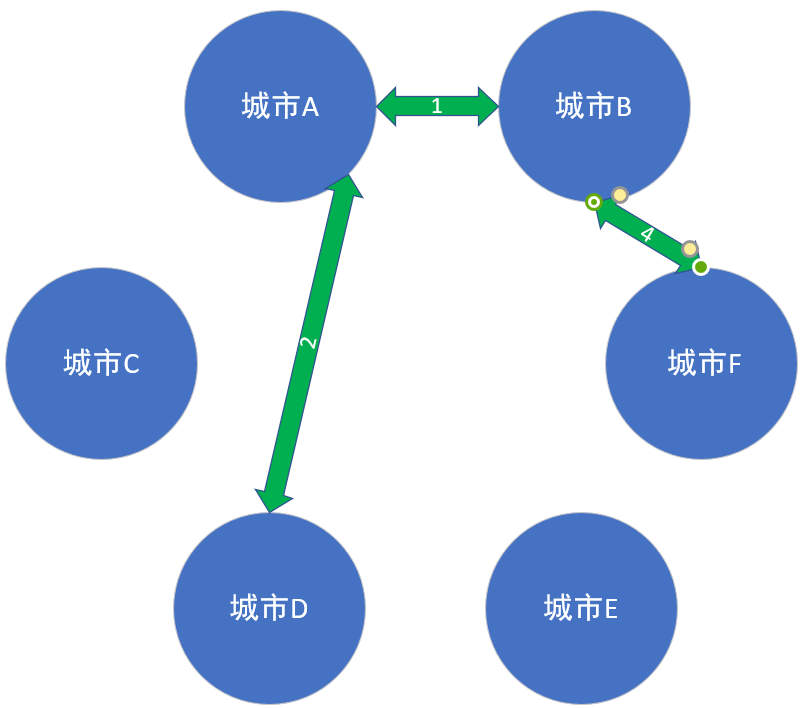
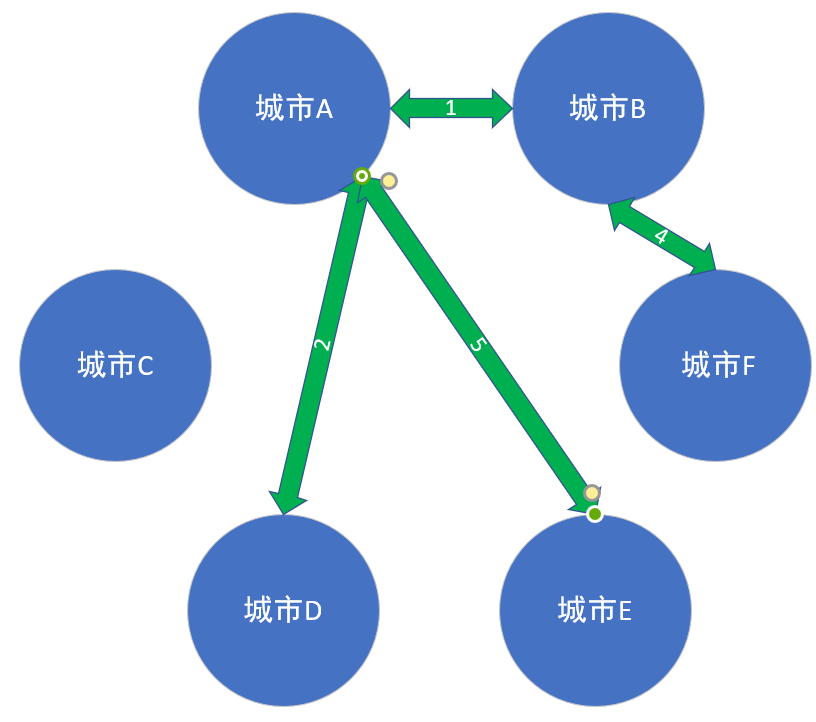
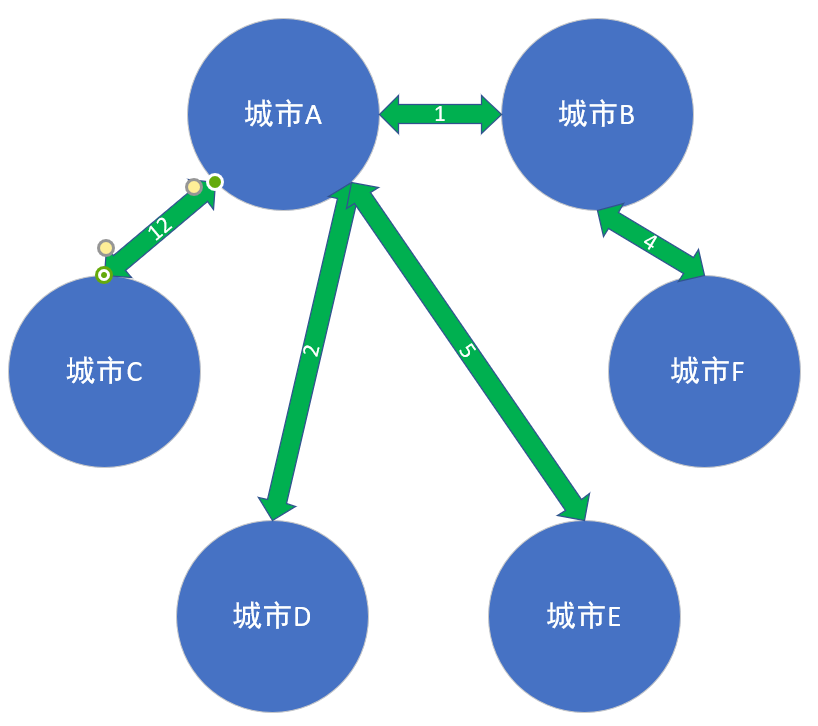
由于我们有六个点,那么我们选择五条边,就完成了我们所需要的最小生成树。没错,这便是我要说的最小生成树的一种算法:(Kruskal 克鲁斯卡尔算法)
比较官方的构造过程便是:
- 假设连通网N=(V,E),将N中的边按权值从小到大的顺序排列
- 初始状态为只有n个顶点而无边的非连通图T=(V,{}),图中每个顶点自成一个连通分量。
- 在E中选择权值最小的边,若该边依附的顶点落在T中不同的连通分量上(即不形成回路),则将此边加入到T中,否则舍去此边而选择下一条权值最小的边
- 重复操作,直到T中所有顶点都在同一连通分量上为止
一波官方的解释,看着我有点懵 (@_@) ,但是没事,我有自己的理解。接下来便是代码实现了......
main.cpp
#include"GraphKruskal.h"
int main()
{
GraphKurskal g1;
g1.Init();
g1.Kruskal();
g1.Display();
return 0;
}
/*
输入样例:
1 1 1
1 4 2
2 6 4
1 5 5
5 6 9
1 3 12
2 3 13
3 4 18
4 5 32
*/
GraphKruskal.h
#pragma once
#ifndef _GRAPHKRUSKAL_H_
#define _GRAPHKRUSKAL_H_
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<vector>
using namespace std;
// 这是利用邻接矩阵来实现的克鲁斯卡尔搜索最小生成树的算法
struct node
{
int from, to;
int sideID;//记录边号,已选定可以输出的边
int distance;
};
class GraphKurskal
{
private:
vector<node>graph;//记录边
vector<bool>visited;//是否经历过
vector<int>IDofSide;//每条边的ID
int minDistacne;//最小权值
int nodeNumber;//几个点
//void Sort();//这个程序是调用库函数的sort函数进行排序,因此没有写自定义sort函数
public:
void Init();//初始化
void Kruskal();//进行克鲁斯卡尔算法,找到最小生成树
void Display();//显示
};
bool cmp(node a1,node a2);//从小到大排序的函数
#endif // !_GRAPHKRUSKAL_H_
GraphKruskal.cpp
#include "GraphKruskal.h"
void GraphKurskal::Init()
{
node n1;
int i = 0;
cout << "请输入有几个点" << endl;
cin >> nodeNumber;
visited.resize(nodeNumber + 1, false);
cout << "请输入各边的关系,'#'结束" << endl;
cout << "请按照格式:开始点---终止点---距离" << endl;
while ((cin >> n1.from&& n1.from != '#') && (cin >> n1.to&& n1.to != '#'))
{
cin >> n1.distance;
n1.sideID = ++i;
graph.push_back(n1);
}
}
void GraphKurskal::Kruskal()
{
sort(graph.begin(), graph.end(),cmp);//进行函数比较
//当选择的边数不为节点数减一的情况,我们继续循环
minDistacne = 0;
for (int i = 0; i < graph.size(); i++)
{
//判断图中的点是否遍历过,如果遍历过,那么跳过,否则继续遍历
if (!visited[graph[i].from] || !visited[graph[i].to])
{
visited[graph[i].from] = true;
visited[graph[i].to] = true;
IDofSide.push_back(graph[i].sideID);
minDistacne += graph[i].distance;
if (IDofSide.size() == nodeNumber - 1)
break;
}
}
}
void GraphKurskal::Display()
{
cout << "总距离是:" << minDistacne << endl<<"权边是:";
for (int i = 0; i < IDofSide.size(); i++)
cout << graph[IDofSide[i]-1].distance << " ";
cout << endl;
}
bool cmp(node a1, node a2)
{
return a1.distance > a2.distance ? false : true;
}
代码实现结果: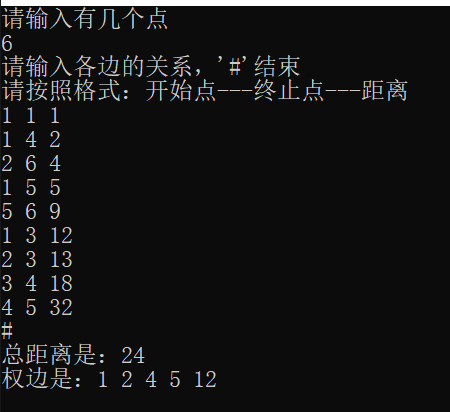
借鉴《数据结构C语言版|第2版》