其实这篇https://www.cnblogs.com/victorique/p/8560656.html写得很完整了,但是为了加深自己的印象,就自己写一篇吧。
网络流的练习我用了传说中的网络流24题,我把题目都看了一遍,发现一个问题,有些题好像真的是为了网络流而搞网络流的做法出来,导致题目的可做性不强,虽然如此,但是除了这些题目之外,其他的题目,也挺让我耳目一新的。
其实,网络流把两套模板给记住,基本上就算是完成了一道题的一大半了。第一套模板是网络最大流(dinic+当前弧优化);第二套模板是最小费用最大流(利用spfa找出最短路的同时保证网络最大流)但是如果像我这么说的话,把网络流单纯看成模板题,是肯定是做不出来题目的,那么网络流关键的点在哪?网络流通常的套路又是什么?
1.建图
基本上网络流的题都难在这里了。如何建图,是一个难点。
(1)二分图

一类建图即是以二分图的形式来建,其包括操作拆点,建立超级源点、汇点,等等。那么在二分图上,能进行解决什么问题呢?最普遍的莫过于匹配问题,通过二分图,求出点与点之间的最大匹配值,然后再利用二分图上的性质,来求出问题的解,而二分图上的性质有下面几种常用的:最大匹配=最小点覆盖;最小路径覆盖=|G|-最大匹配数(G为点数);最大独立集=点数-最大匹配=最小边覆盖。我们可以看到求出一个最大匹配,基本上就能算出其他的问题出来,大多数问题也是基于二分图原理来问的。
例题有:飞行员配对方案问题,试题库问题等,
还有一种类似与二分图的建图方法,其特点是可以从右边的点再回去左边的点,有点像路径问题,但是也不全是,把图画出来其实也大概是上面那个图的模样,应该算是一个变种吧。
例题:数字梯形问题的第一问
(2)普通图
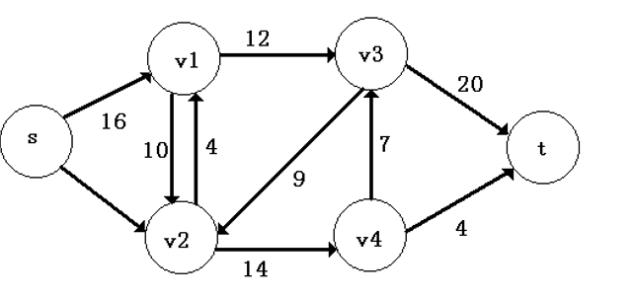
这种图就不说了,应该是网络流题目里面最基础的图。
(3)序列上的图
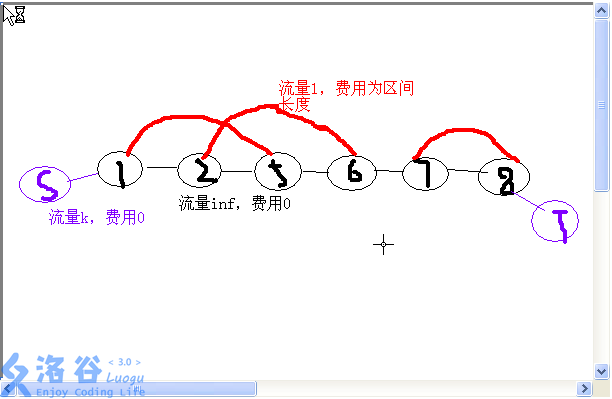
(侵删)
这些题并不类似于我们平时做的网络流题,它是在序列上的,且很难建出来二分图,因此只能让它待在序列上。由于只接触了一道这种题目,而且还是不太理解的那种,这里就只给出一道例题来参考。
例题:最长k可重区间集问题
2.网络流的模型
最小割,最小费用最大流,最大费用最大流等等。(笔者突然这里不想写了,因为开头那篇文章太详细了,感觉写下去都是别人的影子,建议做完网络流的都来围观dalao总结)
总结:刷最大流题目,首先懂得要怎么去建图,把图建好,套上模板,基本上不会出大问题,这里我留下一个疑问,这是我在某个题解的评论里面看到的,原话是:费用流能解决所有线性规划问题,不知是真是假......