由二叉树的定义可知,一棵二叉树由根结点、左子树和右子树三部分组成。因此,只要遍历了这三个部分,就可以实现遍历整个二叉树。若以D、L、R分别表示遍历根结点、左子树、右子树,则二叉树的递归遍历可以有一下三种方式:
先序遍历(DLR)
先序遍历的递归过程为
(1)访问根结点
(2)先序遍历根结点的左子树
(3)先序遍历根结点的右子树
举例: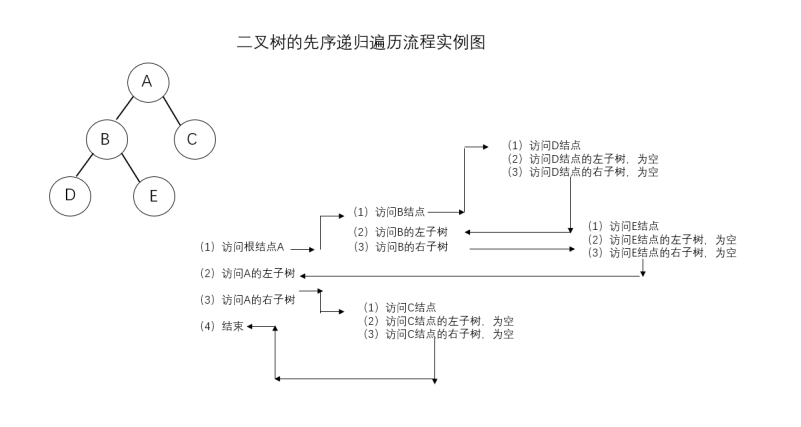
代码:
void PreOrder(BiTree bt)
{
if(bt ==NULL)return; //递归的结束条件----某结点为空时
printf("bt->data); //这里用printf data表示访问结点的数据域
PreOrder(bt->lchild); //递归遍历左孩子
PreOrder(bt->rclild); //递归遍历右孩子
}
中序遍历(LDR)
(1)中序遍历根结点的左子树
(2)访问根结点
(3)中序遍历根结点的右子树
举例: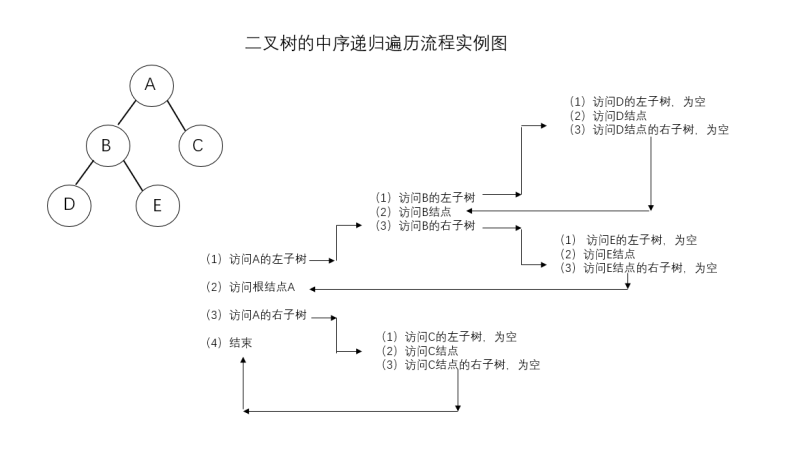
代码:
void PreOrder(BiTree bt)
{
if(bt ==NULL)return; //递归的结束条件----某结点为空时
PreOrder(bt->lchild); //递归遍历左孩子
printf("bt->data); //这里用printf data表示访问结点的数据域
PreOrder(bt->rclild); //递归遍历右孩子
}
后序遍历(LRD)
(1)后序遍历二叉树的左子树
(2)后序遍历二叉树的右子树
(3)访问根结点。
举例: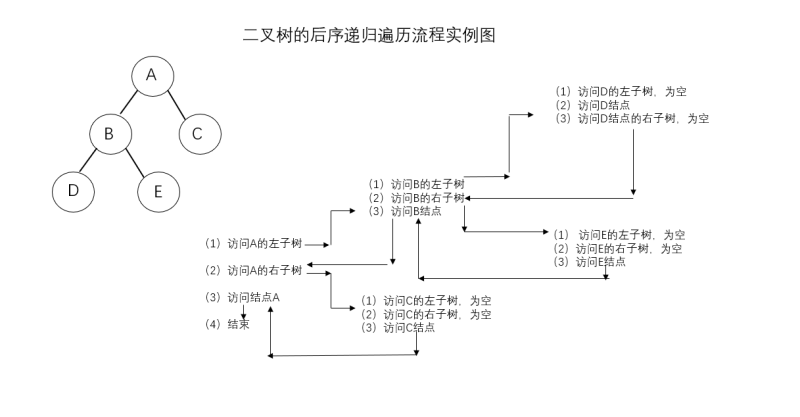
代码:
void PreOrder(BiTree bt)
{
if(bt ==NULL)return; //递归的结束条件----某结点为空时
PreOrder(bt->lchild); //递归遍历左孩子
PreOrder(bt->rclild); //递归遍历右孩子
printf("bt->data); //这里用printf data表示访问结点的数据域
}
层次遍历
(1)根结点入栈
(2)根结点出栈,根结点的左子树、右子树相继入栈
(3)根结点的左子树结点出栈,左子树结点的左子树、右子树相继入栈
(4).......
举例: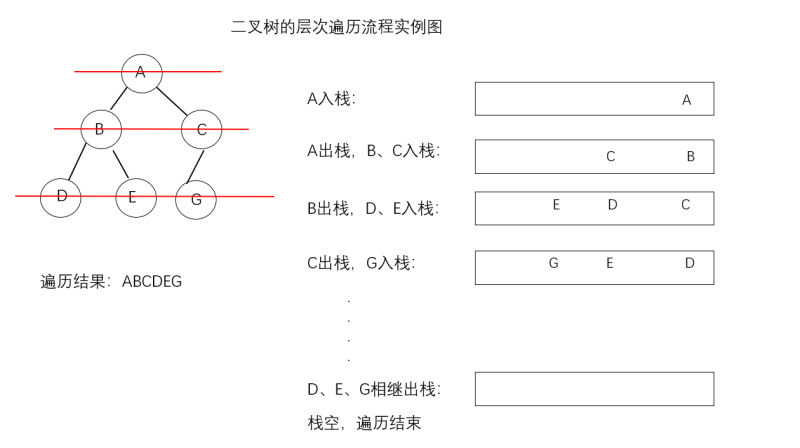
代码:
//层次遍历二叉树
void LevelOrder(BiTree T)
{
BiTree Queue[MAX],b; //用一维数组表示队列,front和rear表示队首和队尾的指针
int front,rear;
front=rear=0;
if(T)
//若树为空
{
Queue[rear++]=T; //根节点入队列
while(front!=rear) //当队列非空
{
b=Queue[front++]; //队首元素出队列,并访问这个节点
printf("%2c",b->data);
if(b->lchild!=NULL) Queue[rear++]=b->lchild ; //若左子树非空,则入队列
if(b->rchild!=NULL) Queue[rear++]=b->rchild ; //若右子树非空,则入队列
}
}
}
最终代码:
#include<stdio.h>
#include<stdlib.h>
#define MAX 20
typedef char TElemType;
typedef int Status;
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild; //左右孩子的指针
} BiTNode,*BiTree;
//先序创建二叉树
void CreateBiTree(BiTree *T)
{
char ch;
ch=getchar();
if(ch=='#')(*T)=NULL; //#代表空指针
else
{
(*T)=(BiTree)malloc(sizeof(BiTNode)); //申请节点
(*T)->data=ch; //生成跟节点
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
//先序输出二叉树
void PreOrder(BiTree T)
{
if(T)
{
printf("%2c",T->data); //访问根节点,此处为输出根节点的数据值
PreOrder(T->lchild); //先序遍历左子树
PreOrder(T->rchild); //先序遍历右子树
}
}
//中序输出二叉树
void InOrder(BiTree T)
{
if(T)
{
PreOrder(T->lchild);
printf("%2c",T->data);
PreOrder(T->rchild);
}
}
//后序输出二叉树
void PostOrder(BiTree T)
{
if(T)
{
PreOrder(T->lchild);
PreOrder(T->rchild);
printf("%2c",T->data);
}
}
//层次遍历二叉树
void LevelOrder(BiTree T)
{
BiTree Queue[MAX],b; //用一维数组表示队列,front和rear表示队首和队尾的指针
int front,rear;
front=rear=0;
if(T)
//若树为空
{
Queue[rear++]=T; //根节点入队列
while(front!=rear) //当队列非空
{
b=Queue[front++]; //队首元素出队列,并访问这个节点
printf("%2c",b->data);
if(b->lchild!=NULL) Queue[rear++]=b->lchild ; //若左子树非空,则入队列
if(b->rchild!=NULL) Queue[rear++]=b->rchild ; //若右子树非空,则入队列
}
}
}
//求树的深度
int depth(BiTree T)
{
int dep1,dep2;
if(T==NULL) return 0;
else
{
dep1=depth(T->lchild);
dep2=depth(T->rchild);
return dep1>dep2?dep1+1:dep2+1;
}
}
int main()
{
BiTree T=NULL;
printf("\n 创建一棵二叉树: \n");
CreateBiTree(&T); //创建二叉树
printf("\n先序遍历的结果为:\n");
PreOrder(T); //先序遍历
printf("\n中序遍历的结果为:\n");
InOrder(T); //中序遍历
printf("\n 后序遍历的结果为: \n");
PostOrder(T);
printf("\n 层次遍历的结果为: \n");
LevelOrder(T); //层次遍历
printf("\n 树的深度为:%d\n",depth(T));
}
结果示例: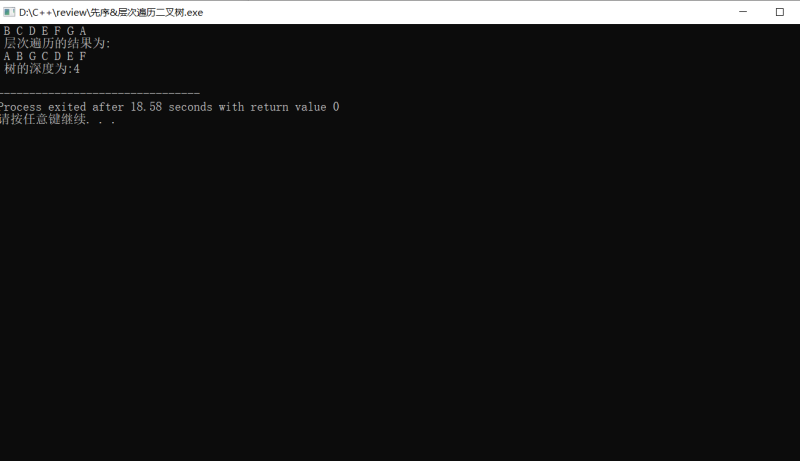
啊,你们不会又打算白嫖吧,点赞呢,关注呢?