函数\(y=\sqrt{3}\left(\dfrac{x}{3}-\dfrac{2}{x}\right)\)图象为双曲线,则其焦点坐标为\(\underline{\qquad\qquad}\).
解析:
法一 显然,该双曲线关于原点中心对称,但其焦点并未在坐标轴上,现拟将该双曲线通过旋转变换,使得新双曲线的焦点位于坐标原点.再反解出旋转变换前的焦点坐标.设将原双曲线绕着原点逆时针旋转\(\theta\),设旋转后的双曲线上任意点的坐标为\((a,b)\),则旋转前坐标\((x,y)\)与旋转后坐标\((a,b)\)有如下关系\(:\)
\[
\begin{cases}
&x=a\cos\theta+b\sin\theta,\\
&y=-a\sin\theta+b\cos\theta,
\end{cases}
\]
代入原函数表达式可得\[
A\cdot a^2+B\cdot b^2+C\cdot ab+D=0.\]其中\[
\begin{cases}
& A=\cos^2\theta+\sqrt{3}\sin\theta\cos\theta,\\
& B=\sin^2\theta-\sqrt{3}\sin\theta\cos\theta,\\
& C=\sin2\theta-\sqrt{3}\cos2\theta,\\
& D=-6,
\end{cases}
\]若要使得旋转后的双曲线的焦点位于坐标轴上,则交叉项的系数必须为\(0\),也即\(C=0\),又即\[
\sin2\theta-\sqrt{3}\cos2\theta=0.\]因此\(\theta\)的一个解为\(\dfrac{\pi}{6}\).此时\[
(A,B,C)=\left(\dfrac{3}{2},-\dfrac{1}{2},-6\right).\]于是将原双曲线绕着坐标原点逆时针旋转\(\dfrac{\pi}{6}\)后的双曲线方程为\[
\dfrac{a^2}{4}-\dfrac{b^2}{12}=1.\]新双曲线的焦点坐标为\((\pm 4,0)\).于是可得旋转前双曲线的焦点坐标为[
\begin{cases}
&x=a\cos\theta+b\sin\theta=\pm 2\sqrt{3},\
&y=-a\sin\theta+b\cos\theta=\mp 2,
\end{cases}
]因此所求双曲线的焦点坐标为\(\left(2\sqrt{3},-2\right)\)与\(\left(-2\sqrt{3},2\right)\).
法二 易知,函数\(y=\sqrt{3}\left(\dfrac{x}{3}-\dfrac{x}{2}\right)\)的两条渐近线为\(x=0\)与\(y=\dfrac{x}{\sqrt{3}}\).
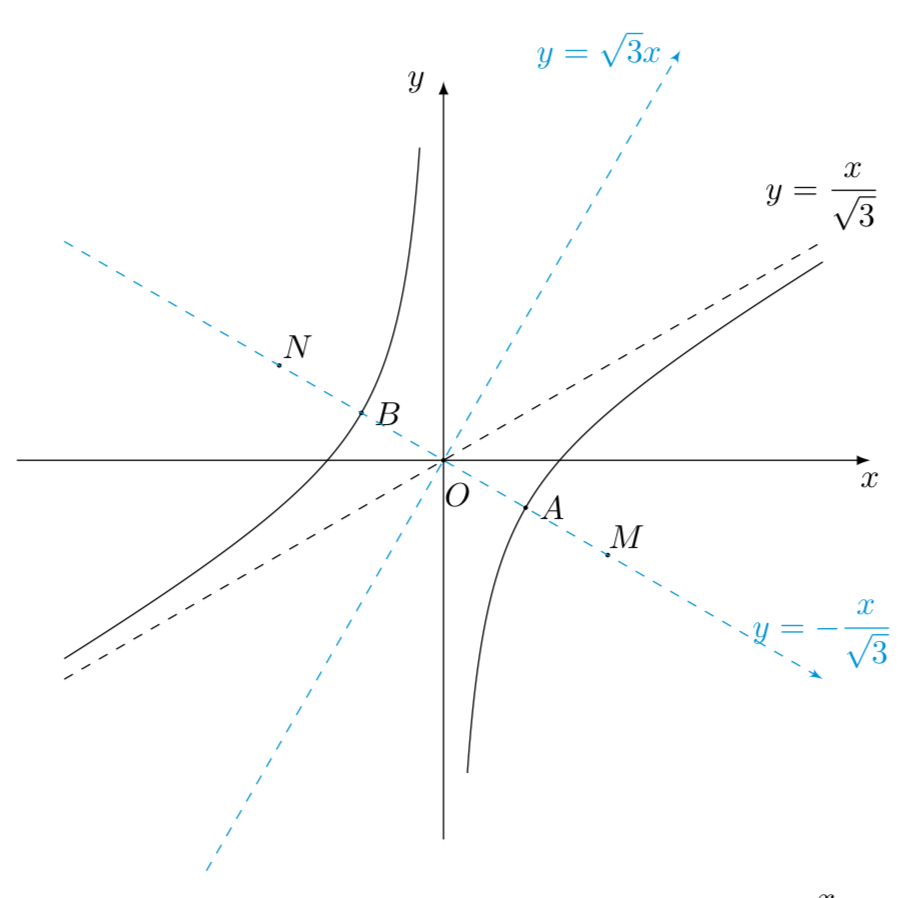
作这两条渐近线的两条角平分线\(y=\sqrt{3}x\)与\(y=-\dfrac{x}{\sqrt{3}}\),若将双曲线放置于这两条角平分线所构成的平面直角坐标系中,则该双曲线的焦点位于直线\(y=-\dfrac{x}{\sqrt{3}}\)上,记为\(M,N\),\(A,B\)为该双曲线的实轴端点.若记新坐标系下的双曲线方程为\[ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1,a,b>0.\]记半焦距为\(c\),则易知\[ \begin{cases} &|AB|=2a=4,\\ &\dfrac{b}{a}=\sqrt{3}. \end{cases} \]
解得\((a,b)=(2,2\sqrt{3})\),从而\[ |MN|=2c=2\sqrt{a^2+b^2}=8.\]于是易得两焦点也即\(M,N\)的坐标为\[ M(2\sqrt{3},-2),N(-2\sqrt{3},2).\]