排序算法之归并排序

归并排序

基本思想

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。利用将已有序的子序列合并，得到完全有序的序列进行排序；即先使每个子序列有序，再使子序列段间有序。然后继续进行归并直到最后整个序列有序。

排序过程

算法首先将待排序序列均分为两部分，然后对于每部分继续均分下去，直到划分为不可分割的一个元素为止；然后按照分割的逆向进行归并，归并两个分组时，依次比较两个分组内的元素的大小，以此来进行排序操作，当一次归并排序完成后，继续和其他的分组以相同的方式进行归并，直到归并为一整个待排序序列，此时整个序列便已经有序，算法结束。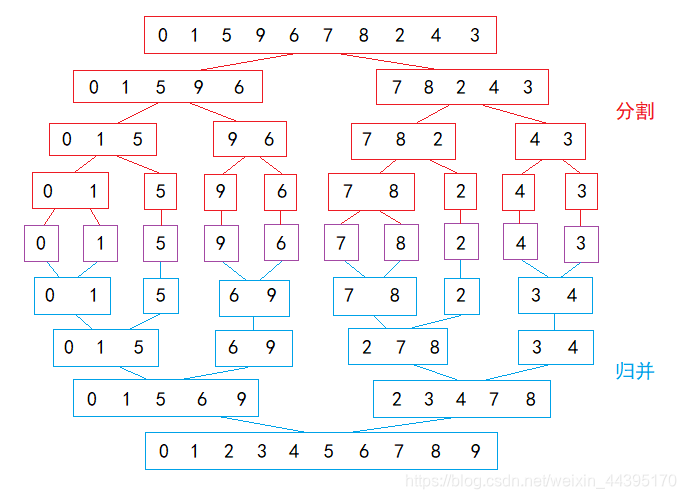

C语言代码实现

递归方式实现：

// 升序排序
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left == right)
		return;

	int mid = left + (right - left) / 2;
	// [left, mid] [mid + 1, right] 分别有序
	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);

	// [left, mid] [mid + 1, right] 归并到tmp[left, right]
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1];
			++begin1;
		}
		else
		{
			tmp[i++] = a[begin2];
			++begin2;
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1];
		++begin1;
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2];
		++begin2;
	}

	memcpy(a + left, tmp + left, sizeof(int)*(i - left));
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

非递归方式实现（利用循环）：

// 升序排序
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);

	int gap = 1;
	while (gap < n)
	{
		// [begin, end]
		for (int begin = 0; begin < n; begin += 2 * gap)
		{
			// [begin, begin+gap-1] [begin+gap, begin+2*gap-1]
			int begin1 = begin, end1 = begin + gap - 1;
			if (end1 >= n)
				end1 = n - 1;

			int begin2 = begin + gap, end2 = begin + 2 * gap - 1;
			if (end2 >= n)
				end2 = n - 1;

			int index = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
					tmp[index++] = a[begin1++];
				else
					tmp[index++] = a[begin2++];
			}

			while (begin1 <= end1)
				tmp[index++] = a[begin1++];
			while (begin2 <= end2)
				tmp[index++] = a[begin2++];
		}
		memcpy(a, tmp, sizeof(int)*n);

		gap *= 2;
	}
	free(tmp);
}

时间复杂度

归并排序同样利用递归算法的时间复杂度计算方法进行计算，归并排序的过程是先二分分解直到为单独的元素，然后进行归并，此时的递归树是一颗二叉树，这棵树的总节点数为待排序的元素个数N，所以归并排序的时间复杂度为O(N*logN)。

空间复杂度

由于进行归并时消耗了和原序列一样大小的空间用于临时存储，所以归并算法的空间复杂度为O(N)。

稳定性

归并排序是把序列划分成短序列，然后把各个有序的短序列合并成一个有序的长序列，不断合并直到原序列全部有序。在序列最小时1个元素，或2个元素时，1个元素不发生交换，2个元素如果大小相等不进行故意交换，这样就不会破坏稳定性。在之后的合并过程中可以保证如果两个当前元素相等时，把处在前面的序列的元素保存在结果序列的前面，所以，归并排序是稳定的。

来源：https://blog.csdn.net/weixin_44395170/article/details/98212856