WGAN(Wasserstein GAN)
1.传统GAN的问题
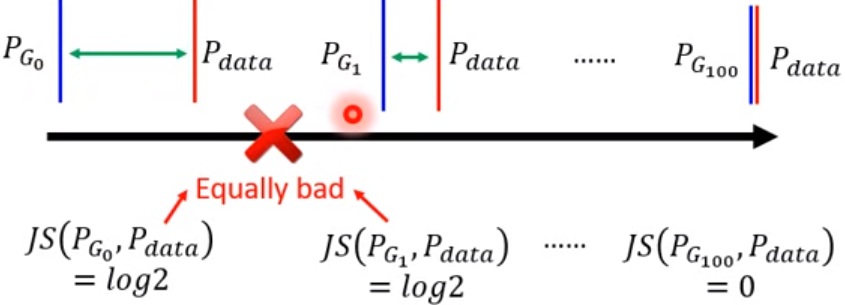
在上一篇学习GAN的博客中，我已经说了GAN所存在的问题，对于从data和artifacts中取样出的x来说，它们的分布很难有不可忽略的重叠部分，于是就会导致JS divergence一直取log2这个最大值，意思是Generator生成的样本分布与真实的样本分布是完全没有交集的；例如下图，虽然在我们看来G1到G50的generator已经改进了许多--已经能够生成更加接近真实分布的样本分布了，但是对于Discriminator，它们的交集还是完全不存在，即Discriminator无法分辨出G1和G50的好坏，也就无法提供给Generator一个有效的方向让它去完成Gradient Descent，我们发现这时候JSD的Gradient是0，也就是发生了梯度消失问题。那么现在我们需要一个改进后的目标函数使其能够真正衡量两个分布之间的距离，这个距离也就是今天的Wasserstein Distance.
2.Wasserstein Distance（Earth-Mover Distance）
首先给出Wasserstein Distance的表达式：
乍一看好像很复杂，我也是第一眼看到这个式子完全不知道是什么意思，可以先来打个比方，有一堆土Pr，我们要把这堆土按照要求堆成另外的一个样子Pg，于是对于一堆土我们总能找到许多种不同的方法γ，将它从Pr堆成Pg，将每种方法γ所需要花费的成本，记为||x-y||，于是在穷举过所有的搬土方法γ后，我们可以找到一种最盛成本的搬土方法，将这个搬土方法把Pr搬成Pg的成本叫做这两堆土之间的Wasserstein Distance。
而对于原式，我们可以考虑γ是服从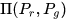
这个联合分布的组合，类比堆土，γ就相当于将Pr中的每一个点与Pg中的每一个点都对应起来，然后计算这种γ下每两个点之间的距离（成本）的期望，这就是其中一个γ的成本，之后我们要穷举所有的Pr和Pg之间的点的对应方法γ，并求出距离（成本）期望最少的那个γ所产生的距离（成本）期望，这个期望就是Wasserstein Distance。
3.Wasserstein Distance 到 WGAN 再到 WGAN-GP
我们已经学习到了Wasserstein Distance的数学表达，但是在实际中直接将Wasserstein Distance作为Generator的loss function是不切实际的，因为我们在每次Gradient Descent的时候都需要求解一个最优的γ，这显然太复杂了，于是WGAN的作者经过复杂的数学推导得到了下面的一个表达式，也就是WGAN的表达式，我们一般用这个式子作为WGAN在训练时的目标函数：
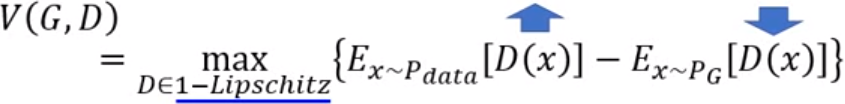
这里的D需要满足1-Lipschitz连续的条件，这个Lipschitz连续的概念我个人感觉有点像高数里的一致连续性的概念的形式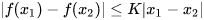
，这个K=1时，就是1-Lipschitz连续，形象一点的说，1-Lipschitz连续就是为了让Generator和Discriminator之间的进化是同步进行的，防止出现由于Discriminator过于powerful以致于Generator无论如何生成，Discriminator总能找到生成数据与真实数据的区别，这样可以让GAN的训练过程更加稳定。当去掉1-Lipschitz连续这个条件时，我们就会发现Discriminator会让第一项一直增大，而Generator会让第二项一直减小，这样这个training是永远不会收敛的。
而在真正的实现过程中，我们发现1-Lipschitz连续这个条件是难以模拟的，以致于WGAN的作者在一开始只能够提出一个十分简化版本的WGAN，这个简化的普通WGAN通过人为的设定一个参数c，当weight>c时,weight=c,当weight<-c时,weight=-c，而这个c的取值时十分重要的，c过大过小都有可能因为神经网络层层之间的递进，发生梯度爆炸或者梯度消失的情况，因此对于参数c的调试是十分繁琐的，这种方法叫做Weight Clipping。
因此后来就出现了另一种模拟Lipschitz连续的方法，也就是WGAN-GP，WGAN-GP引入了新的一项--Gradient Penalty，我们观察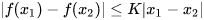这个表达式，我们会发现这个有点像导数的定义，也就是从x1到x2这之间函数的变化率一定要<K,对于WGAN变化率一定要<1，所以我们可以推出，对于每一个点的梯度的模都<1：
。
于是这时WGAN-GP的表达式就是这样：
如果梯度的norm>1，则对原函数加上一个惩罚，如果梯度的norm<1则无惩罚；这就是Gradient Penalty，原本应该对x求一个Gradient Penalty的积分，但是我们可以只用计算Gradient Penalty的期望就可以估计出对目标函数的惩罚了。但我们又可以发现，我们其实不必对每一个x都求一个Gradient Penalty，事实上真正影响我们训练的，只可能是两个分布的点连线上的区域，也就是说只有在我们训练轨迹上的x，才会真正的产生Gradient Penalty，同时，我们也不希望Gradient过低导致训练的过程过于冗长，所以我们希望Gradient最好能够保持在1左右，于是我们可以再对目标函数进行优化，保证Gradient>1或者Gradient<1时都会受到惩罚以保证训练的效率：
有了Loss Function就可以对WGAN-GP进行训练，训练的步骤和GAN基本相同，只需要做出以下改变：
- 判别器最后一层去掉sigmoid
- 生成器和判别器的loss不取log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行
于是WGAN-GP的训练就变成了这样：
4.总结
看完了WGAN之后终于感觉到GAN的强大之处了，就我个人感觉，直接将WGAN硬套用到蛋白质设计方面或许不是个好想法，明天再看看seq-GAN，看一看用seq-GAN做蛋白质设计的那些大佬的文章吧，希望能收到不少启示。
老实说我自己还是不太明白怎么把GAN具体应用到蛋白质设计上。。。。。