摘要
本博文默认读者已经明白了二叉搜索树的插入和删除算法,熟练的掌握左右旋。本文适合掌握BiTree和AVL树的读者,但想学习红黑树的读者。
简介
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
性质
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3. 每个叶结点(NIL)是黑色的
性质4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。——from《算法导论》P174
定义
定义1. 树中的每一个结点具有五个属性:color, key, left, right, p
定义2. 哨兵T.nil是一个树的普通结点,它的color属性为BLACK,其他随意。
定义3. 从某个结点x出发(不含该结点)到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的黑高,记为bh(x)。——from《算法导论》P174
难点
红黑树,通过红黑状态来描述整棵树的平衡情况。它的插入操作和删除操作与基本的二叉搜索树一致,但是增加的对红黑状态的维护和维持树的平衡,即颜色的调整与平衡结构的调整。
插入算法
描述(3case)
插入一个结点,这个结点默认是红色(如果父结点是黑色,几乎不用调整结构)。当其父结点同为红色时需要调整,否则破坏了性质4(每个红色节点的两个子节点都是黑色)。如果它的叔父结点的颜色是红色,那么仅仅通过改变颜色,即可维护红黑性质。否则需要利用左右旋调整结构。
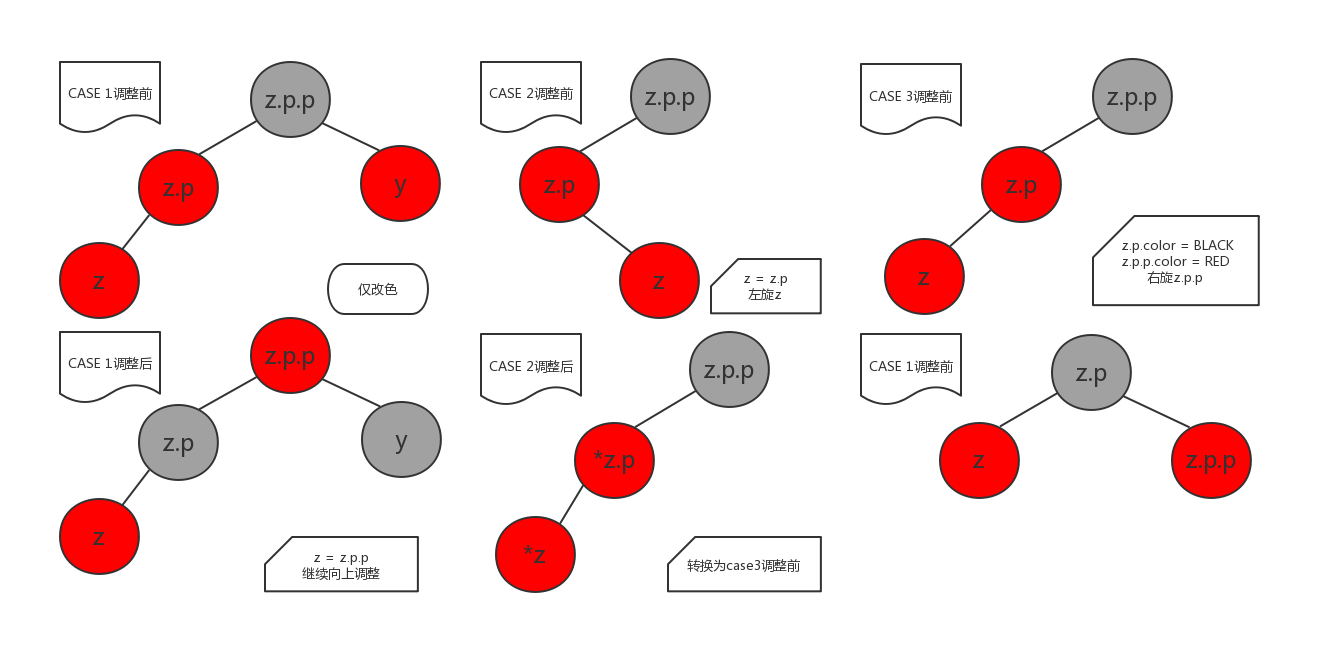
!!!!注意!!!!
case 2调整后的"Z" 为调整前的"Z.P",同理调整后的"Z.P"是调整前的"Z"。
FIXUP伪码
RB-INSERT-FIXUP(T, z)
while z.p.color == RED //父结点红色,违反性质4
if z.p == z.p.p.left //父结点是祖父结点左孩子
y = z.p.p.right //获得叔父结点
if y.color == RED //case 1:父结点和叔父结点同红色
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED //!!注意root.p=NIL NIL.color=BLACK
z = z.p.p //!!自下向上调整
else if z == z.p.right //case 2:z是父结点的右孩子
z = z.p
LEFT-ROTATE(T, z)//左旋完成后由case2变成case3
z.p.color = BLACK //case 3:叔父z是父结点的左孩子
z.p.p.color = RED
RIGHT-ROTATE(T, z.p.p)
else (same as then clause with “right” and “left” exchanged)
//这是一个镜像关系,交换左右旋转条件
T.root.color = BLACK //保持根结点的颜色
注意:
伪码的"else if"与高级语言中的"else if"不同,相当于高级语言的"else {if }"。高级语言中的"else if {}"在伪码中记为"elseif"
删除算法
描述(4case)
讨论以下几个问题:
问1:二叉搜索树的删除操作都做了什么?
答1:删除非叶子结点y,实质上是在y的子孙结点中找到一个结点x代替y。
问2:在红黑树中x替代y,他们的颜色变化有哪几种可能?
答2:四种可能性,记[y.color,x.color],那么有[RED,RED],[RED,BLACK],,[BLACK,RED],[BLACK,BLACK]
问3:这四种变化,会不会影响红黑性质?如果影响了红黑性质,具体破坏哪一条性质?
答3:
[y.color,x.color] 影响的性质 [RED,RED] 没有任何影响 [RED,BLACK] 没有任何影响 [BLACK,RED] 性质2,性质4,性质5 [BLACK,BLACK] 性质5 ——原因参考《算法导论》P184

达成这三个共识,下面的伪码就不难理解了,其中变量y-original-color存储了发生变化前的y颜色

问4:怎样恢复红黑性质呢?
答4:
[y.color,x.color] 解决的办法 [BLACK,RED] 把红涂成黑 [BLACK,BLACK] emmmm
问5:[BLACK,BLACK]怎么破坏了性质5?咋弄?
答5:移动y将导致先前包含y的任何简单路径上黑结点个数少1,因此y的任何祖先都不满足性质5。那么,我们有两条思路:1.把包含y的任何简单路径上增加一个黑色结点(不能破坏其他路径的红黑性质,且这个红色结点只能是y的父结点)2.把其他路径上的一个黑色结点变成红结点。
FIXUP伪码
RB-DELETE-FIXUP(T, x)
while x!= T.root and x.color == BLACK
if x == x.p.left //x为左孩子
w = x.p.right //w是x的兄弟结点
if w.color = RED //case 1:
w.color = BLACK
x.p.color = RED
LEFT-ROTATE(T, x.p)
w = x.p.right //转换为case 2,或者case 3、case 4
if w.left.color == BLACK and w.right.color == BLACK
w.color = RED //case 2:
x = x.p
else
if w.right.color == BALCK
w.left.color = BLACK //case 3:
w.color = RED
RIGHT-ROTATE(T, w)
w = x.p.right //转换为case4
w.color = x.p.color //case 4:
x.p.color = BLACK
w.right.color = BLACK
LEFT-ROTATE(T, x.p)
x = T.root
else (same as then clause with “right” and “left” exchanged)
//这是一个镜像关系,交换左右旋转条件
x.color = BLACK //把红涂成黑
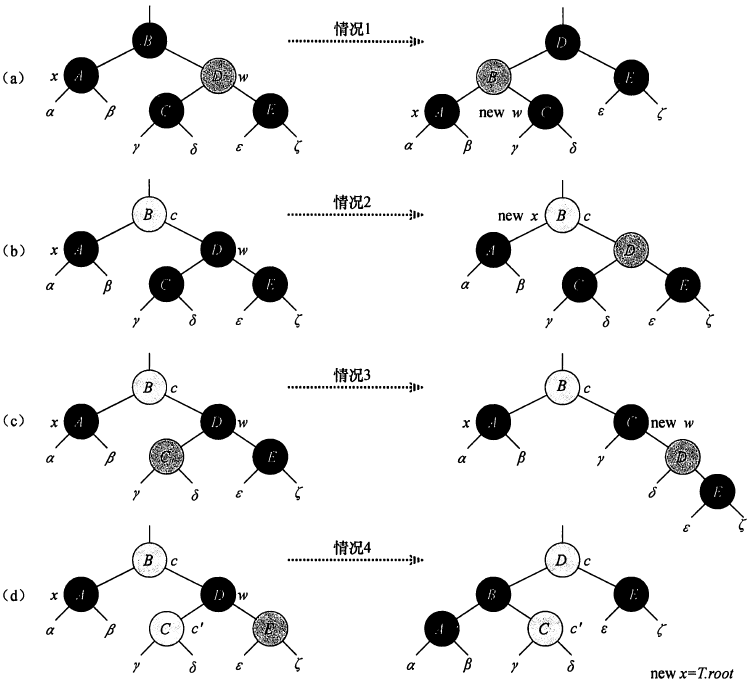
图(a)中A是黑色,D是红色。图(b)中B是红色或者黑色。
再根据伪码分析图:
case 1 :交换了BD颜色,左旋B。调整后ABC构成case 2、case 3 或者case 4的情况(具体取决于c的孩子结点)。
case 2:将D的颜色由黑色改为红色,利用思路2。但是,结点B可能还有兄弟结点,他们的路径也需要你减1。这就相当于回到了问题的起点,利用while循环自下向上调整。
case 3:交换了CD颜色,右旋B。调整后ABCD构成了case 4中的ABDE。
case 4:比较调整完成后Alpha、Beta的路径上的黑结点数,增加了1,其他子树均保持不变。这是思路1的结果。所以直接令x = T.root终止循环
附录 c++ _RB_Tree的调用接口
#include <iostream>
#include <ext/functional>
#include <bits/stl_tree.h> //std::_Rb_tree
#include <bits/stl_function.h>
int main()
{
std::_Rb_tree<int, int, __gnu_cxx::identity<int>, std::less<int>> myTree;
std::cout << myTree.empty() << std::endl; //1
std::cout << myTree.size() << std::endl; //0
myTree._M_insert_unique(3);
myTree._M_insert_unique(8);
myTree._M_insert_unique(5);
myTree._M_insert_unique(9);
myTree._M_insert_unique(13);
myTree._M_insert_unique(5); //not effect, since using _M_insert_unique().
std::cout << myTree.empty() << std::endl; //0
std::cout << myTree.size() << std::endl; //5
std::cout << myTree.count(5) << std::endl;//1
myTree._M_insert_equal(5);
myTree._M_insert_equal(5);
std::cout << myTree.size() << std::endl; //7, since using _M_insert_equal().
std::cout << myTree.count(5) << std::endl;//3
return 0;
}
——参考侯捷老师的讲义
后记
插入和删除算法我花费了3个下午来推理,其中插入算法推理迅速完成。但是我倒在了删除算法的case之中,其中的case列举和转换让我直接迷路。本博客与《算法概论》的唯一不同在,原书将[BLACK,BLACK]破坏的性质5转换破坏性质1,让x结点成为双重黑色的非根结点(这个SmartPoint减小了正向推理过程中的大量分析)。但是我没有采用这样的论述,是因为这样做势必会在四种case分析中讨论这个SmartPoint的妙处,论述难度指数爆炸。所以我采用解说伪码的论述,而不是正向的推理。如果你有兴趣的话,不妨阅读原书仔细体味。