字符串匹配（部分整理）

**加载本页面时，公式可能未渲染（显示乱码）请刷新该页面重试*

问题：给出两串字符

\(text[]="adsgwadsxdsgwadsgz"\)长度为N

\(pattern[]="dsgwadsgz"\)长度为M

查找pattern字符串是否在text出现过并输出所在位置。

一、Brute-Force朴素匹配算法（暴力查找）

时间复杂度\(O(MN)\)

很简单粗暴，碰到稍微长一点的就。。。。。。

图解

代码样例

int i,j
for(i=0; i < strlen(text); i++){
    for(j=0; j < strlen(pattren); j++){
        if(text[i] == pattern[j])
            break;
    }
    if(j == strlen(pattren)){
        printf("Found pattern at %d\n",i-j);
    }
}

二、Rabin-Karp算法（哈西匹配）

时间复杂度\(O(MN)\)，但是实际的速度要更快平均为\(O(M+N)\)

参考OIjulao闫老师的（B站ID: 48833491 ）教学视频

哈希算法就是将一个字符串中的任意子串映分别射到一个实数上面（求子串的时间复杂度为\(O(1)\)）

哈希值的求法就是将字串的p进制数去模q（p常取131、13331，q常取264时哈希值的重复概率要小，这里不需要考虑数的溢出问题）将所有前缀和求出后存放在数组中（这里的数组假设记为hash[]）。求第L到R之间的字符字串的哈希值不难推出为\(hash[R]−hash[L−1]∗p^{L−R+1}\)（后面的要乘的p可以使用数组存一下）

图解

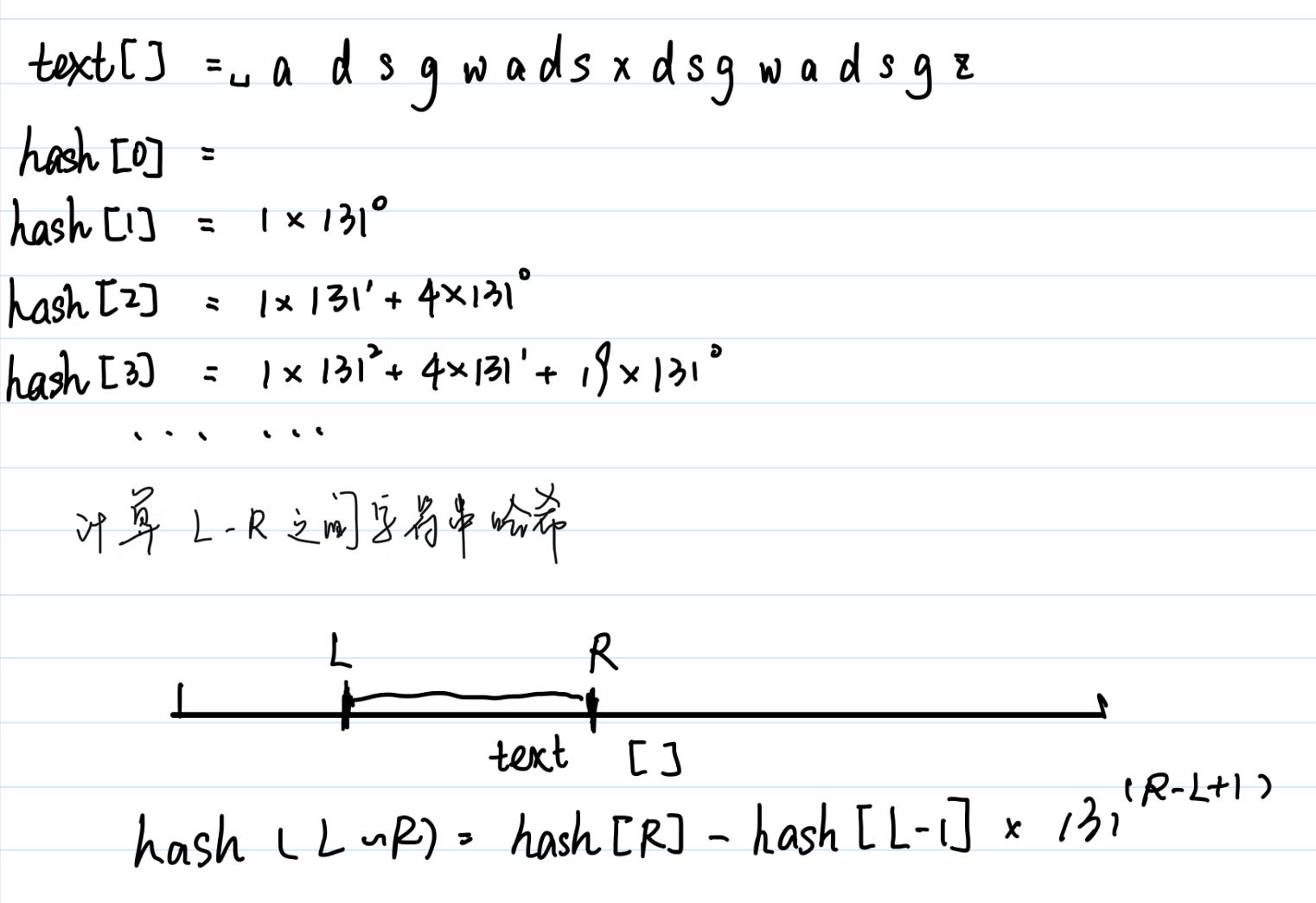
代码样例

计算text前缀的hash

void ha(){
    int len=strlen[text];
    p[0] = 1;
    for(int i=1; i <= len; i++){
        hash[i]=h[i-1] * base + text[i]-'a'+1;
        p[i]=p[i-1]*base;
    }
}

计算text从L到R之间的hash

ULL get(int L,int R){
    return hash[R]-hash[L-1]*p[R-L+1];
}

完整代码

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;

const int manx=1000010,base=131;
char text[maxn],prefix[maxn];
ULL hash[maxn] ,p[maxn];

ULL get(int L,int R){
    return hash[R]-hash[L-1]*p[R-L+1];
}

void ha(){
    int len=strlen[text];
    p[0] = 1;
    for(int i=1; i <= len; i++){
        hash[i]=h[i-1] * base + text[i]-'a'+1;
        p[i]=p[i-1]*base;
    }
}

int main(){
    scanf("%s%s",text+1,prefix);
    ha();
   //这里直接根据题目修改
}

**PS：这里在计算哈希时没有单独的去模一个数，而是直接将hash数组定义为’unsigned long long’。unsigned long long最大值为\(2^{64}\)我们直接使用C++的特点——“如果超出最大表示范围则会自动模一个\(2^{64}\)”，省去单独去模一个数。*

三、KMP算法

时间复杂度\(O(N+M)\)

课本中常见算法

图解（日后更新~）

代码样例

模板采用的是"正月点灯笼"dalao视频教学里的代码

构建prefix（前缀）数组

void prefix_table(char pattern[],int prefix[],int n){
    prefix[0] = 0;
    int len = 0;
    int i = 1;
    while(i<n){
        if(pattern[i] == pattern[len]){
            len++;
            prefix[i] = len;
            i++;
        }
        else{
            if(len > 0)
                len = prefix[len - 1];
            else{
                prefix[i] = len;
                i++;
            }
        }
    }   
}

为了前后更加容易理解，这里将数组偶一以位。

void move_prefix_table(int prefix[],int n){
    int i;
    for (int i=n-1;i>0;i--){
        prefix[i]=prefix[i-1];
    }
    prefix[0] = -1;     
}

KMP查找

void kmp_search(char text[],char pattern[]){
    int n = strlen(pattern);
    int m = strlen(text);
    int* prefix = malloc(sizeof(int) * n);
    prefix_table(pattern,prefix,n);
    move_prefix_table(prefix,n);
    int i=0,j=0;
    while(i<m){
        if(j == n-1 && text[i] == pattern[j]){
            printf("Found pattern at %d\n",i-j);
            j = prefix[j];
        }
        if(text[i] == pattern[j]){
            i++;j++;
        }  
        else{
            j = prefix[j];
            if(j == -1){
                i++;j++;
            }
        }
    }
}

四、Boyer-Moore算法

时间复杂度\(O(N)\)

这是一个比kmp要高效的算法。

由于网上大多数是利用好字符坏字符的规则来进行的讲解，但是这样太繁琐了。这里借鉴arthur.dy.ee的这篇文章思路

图文解

这里还有一种情况，就是当子串中有x字母时，我们则需要将这两个位置=对齐后重复上述步骤即可。

代码样例

代码转自Angel_Kitty

#include <stdio.h>
#include <string.h>

#define MAX_CHAR 256
#define SIZE 256
#define MAX(x, y) (x) > (y) ? (x) : (y)

void BoyerMoore(char *pattern, int m, char *text, int n);

int main()
{
    char text[256], pattern[256];

    while(1)
    {
        scanf("%s%s", text, pattern);
        if(text == 0 || pattern == 0) break;

        BoyerMoore(pattern, strlen(pattern), text, strlen(text));
        printf("\n");
    }
    return 0;
}

void print(int *array, int n, char *arrayName)
{
    int i;
    printf("%s: ", arrayName);
    for(i = 0; i < n; i++)
    {
        printf("%d ", array[i]);
    }
    printf("\n");
}

void PreBmBc(char *pattern, int m, int bmBc[])
{
    int i;
    for(i = 0; i < MAX_CHAR; i++)
    {
        bmBc[i] = m;
    }
    for(i = 0; i < m - 1; i++)
    {
        bmBc[pattern[i]] = m - 1 - i;
    }
/*  printf("bmBc[]: ");
    for(i = 0; i < m; i++)
    {
        printf("%d ", bmBc[pattern[i]]);
    }
    printf("\n"); */
}

void suffix_old(char *pattern, int m, int suff[])
{
    int i, j;
    suff[m - 1] = m;
    for(i = m - 2; i >= 0; i--)
    {
        j = i;
        while(j >= 0 && pattern[j] == pattern[m - 1 - i + j]) j--;

        suff[i] = i - j;
    }
}

void suffix(char *pattern, int m, int suff[]) {
   int f, g, i;
   suff[m - 1] = m;
   g = m - 1;
   for (i = m - 2; i >= 0; --i) {
      if (i > g && suff[i + m - 1 - f] < i - g)
         suff[i] = suff[i + m - 1 - f];
      else {
         if (i < g)
            g = i;
         f = i;
         while (g >= 0 && pattern[g] == pattern[g + m - 1 - f])
            --g;
         suff[i] = f - g;
      }
   }
//   print(suff, m, "suff[]");
}

void PreBmGs(char *pattern, int m, int bmGs[])
{
    int i, j;
    int suff[SIZE];  
    // 计算后缀数组
    suffix(pattern, m, suff);
    // 先全部赋值为m，包含Case3
    for(i = 0; i < m; i++)
    {
        bmGs[i] = m;
    }
    // Case2
    j = 0;
    for(i = m - 1; i >= 0; i--)
    {
        if(suff[i] == i + 1)
        {
            for(; j < m - 1 - i; j++)
            {
                if(bmGs[j] == m)
                    bmGs[j] = m - 1 - i;
            }
        }
    }
    // Case1
    for(i = 0; i <= m - 2; i++)
    {
        bmGs[m - 1 - suff[i]] = m - 1 - i;
    }
//  print(bmGs, m, "bmGs[]");
}

void BoyerMoore(char *pattern, int m, char *text, int n)
{
    int i, j, bmBc[MAX_CHAR], bmGs[SIZE];
    // Preprocessing
    PreBmBc(pattern, m, bmBc);
    PreBmGs(pattern, m, bmGs);
    // Searching
    j = 0;
    while(j <= n - m)
    {
        for(i = m - 1; i >= 0 && pattern[i] == text[i + j]; i--);
        if(i < 0)
        {
            printf("Find it, the position is %d\n", j);
            j += bmGs[0];
            return;
        }
        else
        {
            j += MAX(bmBc[text[i + j]] - m + 1 + i, bmGs[i]);
        }
    }
    printf("No find.\n");
}

来源：https://www.cnblogs.com/cafu-chino/p/11759715.html