起步
非线性回归是线性回归的延伸,线性就是每个变量的指数都是 1,而非线性就是至少有一个变量的指数不是 1。生活中,很多现象之间的关系往往不是线性关系。选择合适的曲线类型不是一件轻而易举的工作,主要依靠专业知识和经验。常用的曲线类型有 幂函数,指数函数,抛物线函数,对数函数和S型函数 。
化非线性回归为线性回归
通过变量代换,可以将很多的非线性回归转化为线性回归。比如目标函数假设是 y = b0 + b1x + b2x^2 。那么另 z1 = x, z2 = x^2 。目标函数就变为 y = b0 + b1z1 + b2z2。就可以用线性回归来解方程了而用上一篇文章《线性回归之多元线性回归》就能解决线性回归的问题。常见的转化模型有:

逻辑回归
逻辑回归是(Logistic Regression)是非线性回归中的一种,在分类问题上有的也能采用逻辑回归分类。这是一个二分器。比如根据肿瘤的大小来判断其良性或恶性,线性方程显然不能够胜任了:
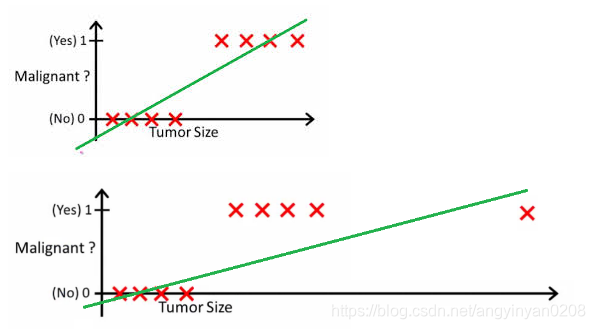
逻辑回归模型中,先给定线性函数:
![]()
虽然这边是 θ 表示,但其实和线性回归中 b 是一个意思,都是作为自变量的系数。在二分类器中,经常需要一个分界线作为区分两类结果。再次需要一个函数进行曲线平滑化,由此引入 Sigmoid 函数进行转化:


这样,以0.5作为分界线。因此逻辑回归的最终目标函数就是:

回归就是用来得到样本属于某个分类的概率。因此在分类结果中,假设y值是0或1,那么正例(y=1):
![]()
反例(y=-1):
![]()
回想起之前线性中用到的损失函数:
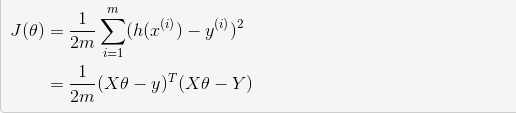
我们的目标很明确,就是找到一组 θ ,使得我们的损失函数 J(θ) 最小。最常用的求解方法有两种:梯度下降法( gradient descent ), 牛顿迭代方法( Newton's method)。两种方法都是通过迭代求得的数值解,但是牛顿迭代方法的收敛速度更加快。牛顿迭代方法在此不介绍。
注:如果在逻辑回归中运用这种损失函数,得到的函数J是一个非凸函数,存在多个局部最小值,很难进行求解,因此需要换一个 COST 函数。重新定义个cost函数如下:
![]()
梯度下降求解逻辑回归
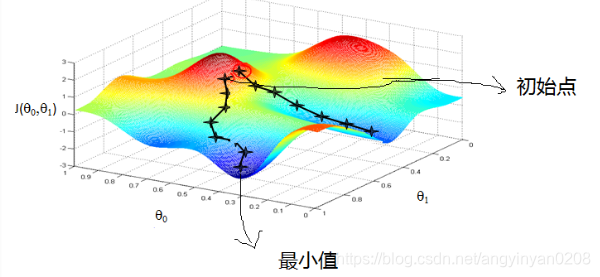
这就好比是下山,下一步的方向选的是最陡的方向。梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。θ 的更新方程如下:

其中偏导数是:
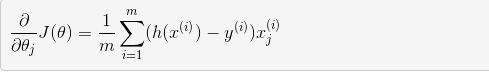
如果将 θ 视为矩阵,可以进行批量更新:
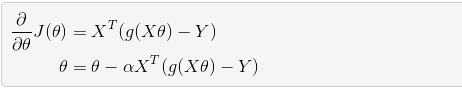
来源:CSDN
作者:angyinyan0208
链接:https://blog.csdn.net/angyinyan0208/article/details/83653498