线段树是一种强大的数据结构,用于维护区间、图、树等各种数据。
线段树的“强大”体现在它面对各种类型的数据都有应付的方式,而且不断有“改进”版线段树的产生。
线段树是基于递归和分治思想的数据结构,一般用于维护具有“区间可加性”的数据。
什么是”区间可加性“呢,举几个例子:
区间和,区间最大最小值,区间LCA,区间质数个数
这些东西都有共同的特性:f(x,y)=f(f(x,z),f(z,y)),z∈[x,y]
于是我们就可以用线段树来维护。
随手画了张线段树的图,它大概长这样:
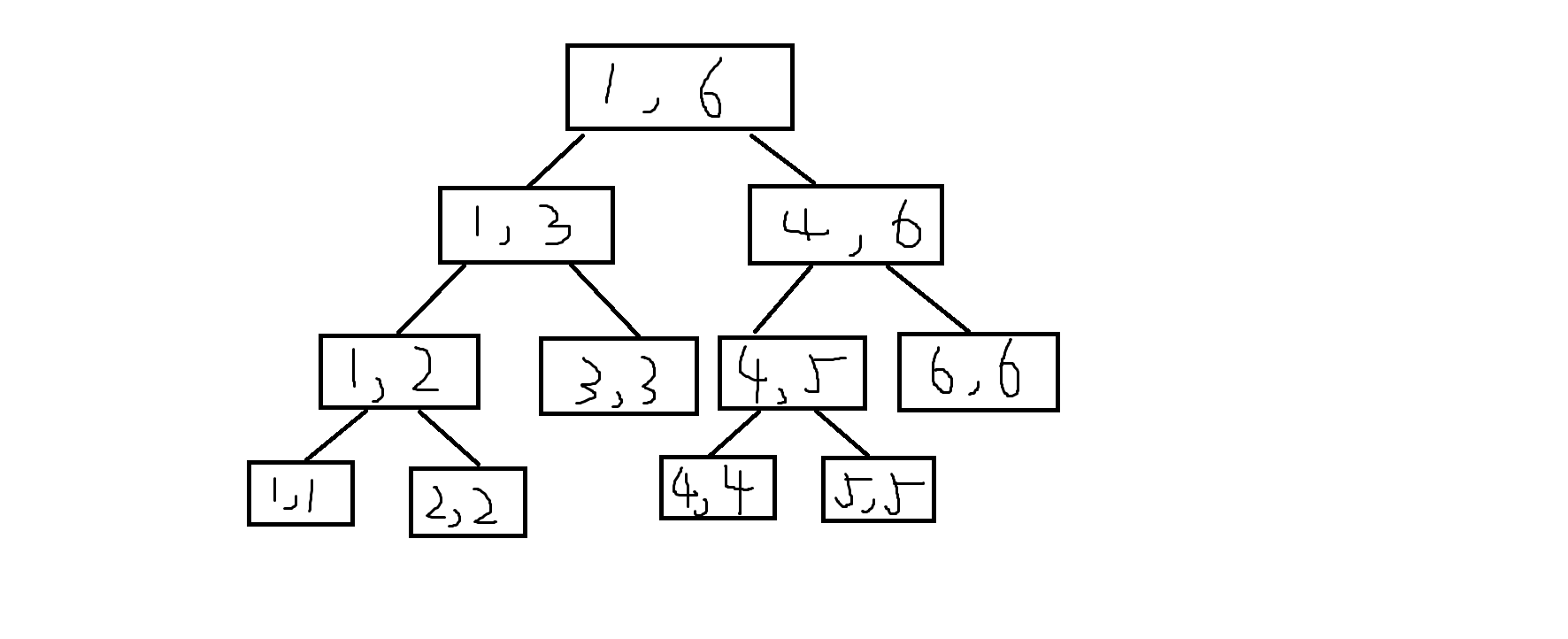
是不是很神奇?
它是怎么维护数据的呢?( 以维护区间数据为例 )
让我们用区间最大值为例:
假设原数组a是{1,2,3,4,5,6} (我习惯下标从1开始)
我们把原数组插入线段树,看看它各个节点的值:

假设我们要查询区间 [2,4] 的值:
我们发现并没有 [2,4] 这个节点,那怎么查询呢?
我们计算出 [2,4] 的mid值,mid=(l+r)/2=3。
然后我们查询区间 [2,3] 和区间 [4,4] ( 即区间[l,mid]和区间[mid+1,r] )。
区间 [4,4] 是叶子节点,返回它的值4。
回到 [2,3] 我们继续递归计算max( [2,2],[3,3] )返回3
得到最后的最大值4
这一段的代码:
int query(int p,int l,int r){
if(l<=l(p) && r>=r(p))return val(p);
int mid=(l(p)+r(p))>>1;
int val=-INF;
if(l<=mid)val=max(val,query(p<<1,l,r));
if(r>mid)val=max(val,query(p<<1|1,l,r));
return val;
}
等等,既然要维护数据,怎么能不支持修改呢?
线段树支持单点修改和区间修改。
单点修改非常简单,我这里就不介绍了。
直接来区间修改。
我们每次更新一个值都要把所有包含它的节点更新一次。
但是如果更新一整个区间,这个更新量是非常大的,作为一种高效数据结构是不会允许这么慢的修改的。
于是我们引进一个”打标记“的思想。
也就是给我们要更新的值先打上”你已经被修改了“的标记,等我们要用它的时候在改它。
在线段树中被称为”下发懒标记“——pushdown lazytag
下传标记的代码( 以维护区间和为例 ):
void pushdown(int p){
if(add(p)){
val(p<<1)+=add(p)*(r(p<<1)-l(p<<1)+1);
val(p<<1|1)+=add(p)*(r(p<<1|1)-l(p<<1|1)+1);
add(p<<1)+=add(p);
add(p<<1|1)+=add(p);
add(p)=0;
}
}
这里我们的懒标记是加(add),懒标记还可以是乘(mul),或者加乘混合(需要符合运算法则)
接下来放建树的代码:
void pushup(int p){
val(p)=val(p<<1)+val(p<<1|1);
}
void build(int p,int l,int r){
l(p)=l,r(p)=r;//保存每个节点的左右儿子的编号
if(l==r){
val(p)=a[l];
return;
}pushdown(p);
int mid=(l+r)>>1;
build(p<<1,l,mid);build(p<<1|1,mid+1,r);//递归建树
pushup(p);//更新值
}
上一份维护区间和的完整代码吧:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int data=0,w=1;char ch=0;
while(ch!='-' && (ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(ch>='0' && ch<='9')data=data*10+ch-'0',ch=getchar();
return data*w;
}//快读
const int maxn=100010;
int n,m,a[maxn];
struct SegmentTree{
int l,r;//左右节点编号
int val,add;//节点值,标记
#define l(x) tree[x].l
#define r(x) tree[x].r
#define val(x) tree[x].val
#define add(x) tree[x].add
}tree[maxn<<2];
void pushup(int p){
val(p)=val(p<<1)+val(p<<1|1);//更新,一个节点用它的左右两个节点更新
}
void build(int p,int l,int r){//建树代码
l(p)=l,r(p)=r;
if(l==r){
val(p)=a[l];return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);build(p<<1|1,mid+1,r);
pushup(p);
}
void pushdown(int p){//下传懒标记
if(add(p)){
val(p<<1)+=add(p)*(r(p<<1)-l(p<<1)+1);
val(p<<1|1)+=add(p)*(r(p<<1|1)-l(p<<1|1)+1);
add(p<<1)+=add(p);
add(p<<1|1)+=add(p);
add(p)=0;
}
}
int query(int p,int l,int r){//查询
if(l<=l(p) && r>=r(p))return val(p);
pushdown(p);
int mid=(l(p)+r(p))>>1;
int ret=0;
if(l<=mid)ret+=query(p<<1,l,r);
if(r>mid)ret+=query(p<<1|1,l,r);
return ret;
}
void update(int p,int l,int r,int d){//修改
if(l<=l(p) && r>=r(p)){
val(p)+=d*(r(p)-l(p)+1);add(p)+=d;
return;
}
pushdown(p);
int mid=(l(p)+r(p))>>1;
if(l<=mid)update(p<<1,l,r,d);
if(r>mid)update(p<<1|1,l,r,d);
pushup(p);
}
int main(){
n=read();m=read();//读入数据个数,操作个数
for(int i=1;i<=n;i++)a[i]=read();//读入数据
build(1,1,n);//建树
int opt,l,r,d;
while(m--){
opt=read();l=read();r=read();
if(opt==1)//查询
printf("%d\n",query(1,l,r));
else{
d=read();//区间加上这个值
update(1,l,r,d);//修改
}
}
return 0;
}