概述

就是可持久化的线段树。更直白一点，就是 很多个线段树套在一起（共用信息相同的节点）。

干嘛

可以解决区间第 $k$ 大等神奇问题。

优点

快。

实现

0x01初始化
一开始，我们需要一颗线段树。就按照普通的建树方法即可。
0x02建新树

要素是 不改变原有的节点。因为本质是很多不同的线段树，只是用一些奇技淫巧来省空间（和时间）而已。
首先，将原来的树的 对应节点复制到当前节点。包括子节点是谁。也就是说，现在这两个点 共用了相同的子节点。
然后考虑子节点——如果有修改，则 申请新节点，递归的建树。否则不动。

在理解这个玩意儿的时候，你就这么想：其实两个点的子节点不同，没有共用子节点，只是子节点住一间屋子而已。反正我们也不会把房子拆了，即修改原有的节点。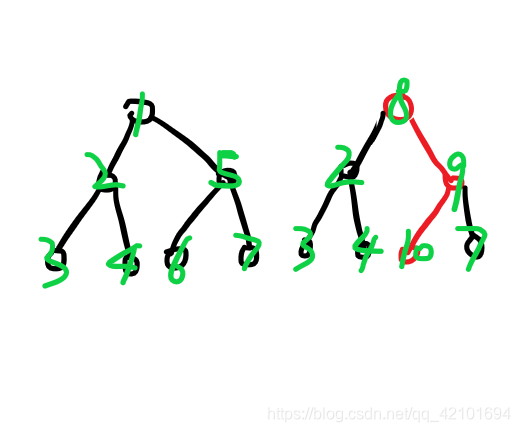
在这里插入图片描述
也就是说，本质是这样的两颗线段树。绿色的编号表示 内存地址。共用内存罢了。
——前提条件是这两个节点 信息相同！
这样做的好处，在 单点修改 时很明显：只需要新建 $\log n$ 个点。因为只有 $\log n$ 这一条单链上的点（即红色的点）与原有的节点信息不同。
或者放点代码？

void modify(int old,int &o,int id){
	o = cntNode ++; // 申请新节点 
	node[o] = node[old]; // 复制旧节点 
	if(node[old].l == node[old].r){ // 叶子节点，直接更改信息
		++ node[o].ppl;
		return ;
	}
	if(id <= (node[o].l+node[o].r)>>1) // 说明右子树与原有的节点信息是相同的
		modify(node[old].lson,node[o].lson,id);
	else // 递归修改子树
		modify(node[old].rson,node[o].rson,id);
	pushUp(o); // 更新当前节点信息
}

但是，就像普通的线段树，任何查询操作都需要 知道根是谁。所以你得用一个 $\text{root}$ 数组把第 $x$ 个线段树的根存下来。

顺便一说，区间修改 就必须使用奇技淫巧了。

标记永久化。就是舍弃 $\text{pushdown}$ ，递归时自己惦记着。
下传也开新点。为了不修改原有节点嘛。

0x03查询
当成普通线段树。——别忘了 ~~人类的本质~~ 主席树的本质就是 ~~真香！~~ 普通线段树的省空间版本。

例题

0x01板题
如题。记得离散化。

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

const int MaxN = 200005;
struct segmentTreeNode{ // 权值线段树
	int lson, rson, l, r;
	int ppl; // PPL orz or2 orz
}node[MaxN<<5];
int root[MaxN], cntNode;
void pushUp(int pos){
	node[pos].ppl = node[node[pos].lson].ppl+node[node[pos].rson].ppl;
}
void build(int &o,int l,int r){
	o = cntNode ++;
	node[o].l = l; node[o].r = r;
	if(l != r){
		build(node[o].lson,l,(l+r)>>1);
		build(node[o].rson,(l+r)/2+1,r);
		pushUp(o);
	}
	else{ // is a leaf
		node[o].ppl = 0;
	}
}
void modify(int old,int &o,int id){
	o = cntNode ++;
	node[o] = node[old];
	if(node[old].l == node[old].r){
		++ node[o].ppl;
		return ;
	}
	if(id <= (node[o].l+node[o].r)>>1)
		modify(node[old].lson,node[o].lson,id);
	else
		modify(node[old].rson,node[o].rson,id);
	pushUp(o);
}
int query(int old,int o,int k){
	if(node[o].l == node[o].r)
		return node[o].l;
	if(node[node[o].lson].ppl-node[node[old].lson].ppl >= k)
		return query(node[old].lson,node[o].lson,k);
	k -= (node[node[o].lson].ppl-node[node[old].lson].ppl);
	return query(node[old].rson,node[o].rson,k);
}

int lsh[MaxN], a[MaxN], n;
int zxyMeier[MaxN];
void getLSH(){
	for(int i=0; i<n; ++i)
		zxyMeier[i] = a[i];
	sort(zxyMeier,zxyMeier+n);
	for(int i=0; i<n; ++i)
		lsh[i] = lower_bound(zxyMeier,zxyMeier+n,a[i])-zxyMeier;
}
int main(){
	int q;
	scanf("%d %d",&n,&q);
	for(int i=0; i<n; ++i)
		scanf("%d",&a[i]);
	getLSH();
	build(root[0],1,n);
	for(int i=1; i<=n; ++i)
		modify(root[i-1],root[i],lsh[i-1]+1);
	for(int i=1,l,r,k; i<=q; ++i){
		scanf("%d %d %d",&l,&r,&k);
		printf("%d\n",zxyMeier[query(root[l-1],root[r],k)-1]);
	}
	return 0;
}

0x02板题二号
题目描述
（阅读程序，猜测题目）
提示：很板！

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int MaxN = 100005;
struct segmentTreeNode{
	int lson, rson, l, r;
	int maxV;
}node[MaxN<<3];
int root[MaxN], cntNode;
int val[MaxN];
void pushUp(int pos){
	node[pos].maxV = max(node[node[pos].lson].maxV,node[node[pos].rson].maxV);
}
void build(int &o,int l,int r){
	o = cntNode ++;
	node[o].l = l; node[o].r = r;
	if(l != r){
		build(node[o].lson,l,(l+r)>>1);
		build(node[o].rson,(l+r)/2+1,r);
		pushUp(o);
	}
	else
		node[o].maxV = val[l];
}
void modify(int old,int &o,int id,int v){
	o = cntNode ++;
	node[o] = node[old];
	if(node[old].l == node[old].r){
		node[o].maxV = v;
		return ;
	}
	if(id <= (node[old].l+node[old].r)>>1)
		modify(node[old].lson,node[o].lson,id,v);
	else
		modify(node[old].rson,node[o].rson,id,v);
	pushUp(o);
}
int query(int o,int l,int r){
	if(l <= node[o].l and node[o].r <= r)
		return node[o].maxV;
	if(r <= (node[o].l+node[o].r)>>1)
		return query(node[o].lson,l,r);
	if(l > (node[o].l+node[o].r)>>1)
		return query(node[o].rson,l,r);
	return max(query(node[o].lson,l,r),query(node[o].rson,l,r));
}

int main(){
	int n, q;
	scanf("%d %d",&n,&q);
	for(int i=1; i<=n; ++i)
		scanf("%d",&val[i]);
	build(root[1],1,n);
	int edition = 1;
	while(q --){
		int cmd, k, one, two;
		scanf("%d %d %d %d",&cmd,&k,&one,&two);
		if(cmd == 0)
			printf("%d\n",query(root[k],one,two));
		else
			modify(root[k],root[++ edition],one,two);
	}
	return 0;
}

来源：https://blog.csdn.net/qq_42101694/article/details/102754746

标签

主席树

【学习笔记】主席树

概述

干嘛

优点

实现

例题