SVM算法（六）SVM算法的正则化损失函数视角

一、用“损失函数+正则项”理解SVM最优化目标

如近似线性可分问题所述，SVM算法的目标是求得如下目标函数的最小值：$\begin{aligned}&\min\frac{1}{2}w^2+C\sum\limits_{i=1}^n \xi_i \\&s.t.\space \space y_i(wx_i+b)\ge1-\xi_i\\ &\qquad \xi_i \ge0\end{aligned}$根据拉格朗日广义函数对偶问题的分析，$\alpha_i$共有如下三种取值情况：
1）$\alpha_i=C$，由对偶互补条件有$\xi_i=1-y_i(wx_i+b)$
2）$\alpha_i=0$，由对偶互补条件有$\xi_i=0$
3) $0<\alpha_i<C$，对应于支持向量边界上的点，显然$\xi_i=0$
所以，上述最优化问题可写成：$\min\frac{1}{2}w^2+C\sum_{i=1}^n\max(0, 1-y_i(wx_i+b))$或进一步可写成：$\min\frac{1}{2C}w^2+\sum_{i=1}^n\max(0, 1-y_i(wx_i+b))$该公式可以理解为某个损失函数$\max(0, 1-y_i(wx_i+b))$与$L2$正则项的和作为目标函数，惩罚项$\lambda=\frac{1}{2C}$
也就是说，SVM的目标可以理解为最小化$L2$正则化下的损失函数$\max(0, 1-y_i(wx_i+b))$，这个损失函数称为合页损失函数（Hinge Loss）。

二、合页损失函数

SVM的损失函数为合页损失函数：$\max(0, 1-y(wx+b))$该损失和0-1损失、log损失（以2为底）、平方损失等常见损失的对比见下图。

在分类问题中，0-1损失是最容易想到的损失函数（判断错统一惩罚1，不管错的多离谱），而上图中的其它损失函数都是0-1损失的上界。

对于合页损失，其对判断正确和错误处的惩罚力度均进行了调整：1）不光要判断正确，而且函数距离必须大于1（可以理解为正确的可信度高，即margin=1）才无须惩罚；2）对于判断错误，或者虽然判断正确但可信度不高的值，均进行惩罚，且错的越多，惩罚力度随之线性增加。

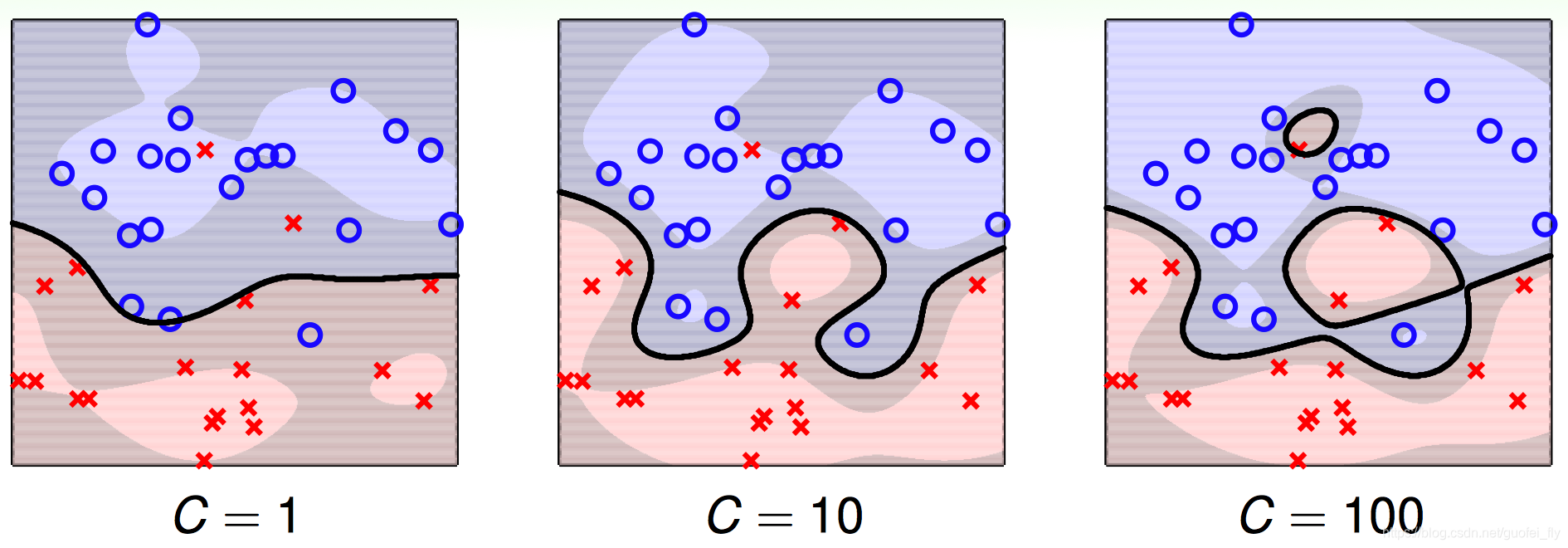
三、参数C的意义

在前文的推广中，将参数$C$定义为对间隔进行松弛$\xi$时的惩罚项。当$C$越大时，越不允许有过大的$\xi$，因此分割平面必须越能正确的区分每个数据点，所以分割平面越复杂，越可能导致过拟合。

从正则化损失函数的角度来思考，因为$L2$正则化前的系数$\lambda=\frac{1}{2C}$，$C$越大意味着$\lambda$越小，对假设空间复杂度的约束越小，边界也就越复杂。这与上面的结论相一致。

四、线性模型$L2$正则化的泛化

回到SVM的正则化损失函数表达形式：$\min\frac{1}{2C}w^2+\sum_{i=1}^n\max(0, 1-y_i(wx_i+b))$与之类似的，还有添加$L2$正则项之后的逻辑损失问题和线性回归问题：$\begin{aligned} &\min \lambda w^2+\sum_{i=1}^ny_i\sigma(x_i)+(1-y_i)(1-\sigma(x_i))\\&\min\lambda w^2+\sum_{i=1}^n(y_i-wx_i-b)^2\end{aligned}$不难得到在线性模型基础上，进行$L2$正则化的泛化表达形式：$\min \lambda w^2+\sum_{i=1}^nerr(y_i,g(wx_i))$式中$g(wx)$表示线性模型。
通过这种泛化，我们可以通过调整损失函数以适应不同的问题，还可以将SVM中核技巧推广到其它的线性模型。这也是后文介绍SVM概率模型和SVM回归模型的基础。

来源：https://blog.csdn.net/guofei_fly/article/details/102750900