4_神经网络优化,y=x1+x2

1 神经元模型：

上一节神经网络不算完整,因为计算公式应该是y=add (xi*wi + b)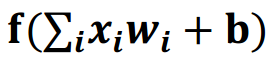

2、激活函数

引入非线性激活因素，提高模型的表达力。

常用的激活函数有：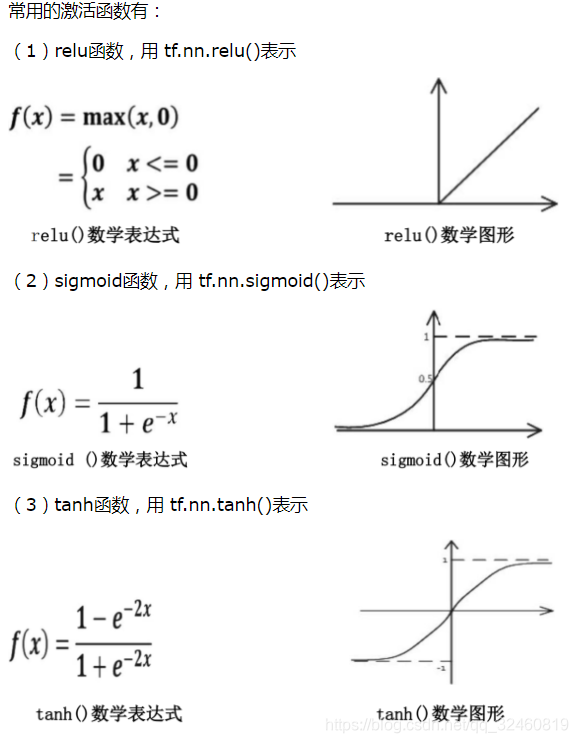

3、神经网络的复杂度

可以用神经网络的层数和神经网络待优化的参数个数来表示

4、神经网络的层数

层数=n个隐藏层 + 1个输出层

注意：一般不计入输入层

5、神经网络待优化的参数

神经网络所有参数w、b的个数

举例：下图为神经网络示意图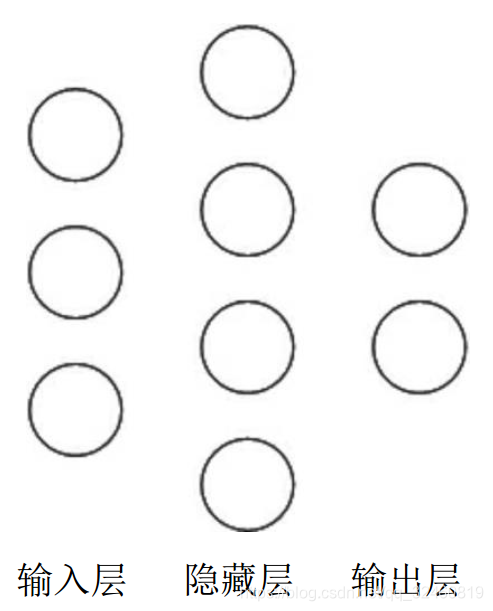

在该神经网络中，包含1个输入层、1个隐藏层和1个输出层，该神经网络的层数为2层。(不计入输入层)

在该神经网络中，参数的个数是所有参数w的个数加上所有参数b的总数，第一层参数用三行四列的二阶张量表示（即12个线上的权重w）再加上4个偏置b；第二层参数是四行两列的二阶张量（即8个线上的权重w）再加上2个偏置b。总参数=34+4+42+2=26。

第二次循环,神经网络优化,奶销量

在本篇文章中我们用一个预测酸奶日销量 y 的例子来验证神经网络优化的效果。x1、x2是影响日销量的两个因素。由于目前没有数据集，所以利用随机函数生成x1、x2，制造标准答案y_=x1+x2，为了更真实，求和后还添加了正负0.05的随机噪声。

选择mse的损失函数，把自制的数据集喂入神经网络，构建神经网络，看训练出来的参数是否和标准答案y_ = x1+x2

import tensorflow as tf
import numpy as np
#import
batch_size = 8
seed = 23455
print("start")

#构造数据集
rdm = np.random.RandomState(seed)#随机数生成器
X = rdm.rand(32,2)#32行,2列
# print("X=\n",type(X),"\nvalue:\n",X )
Y_ = [ [ x1+x2 + (rdm.rand()/10.0  - 0.05) ] for (x1, x2) in X ]  
#rand 构造0-1 随机数, 除10以后,构造0-0.1的随机数, 在减0.05变成-0.05 - 0.05随机数
#即噪声是 y=x1+x2+(正负0.05)

# print(Y_)

#输入
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None,1))

#待优化参数
w1 = tf.Variable(tf.random_normal( [2,1], stddev=1, seed=1 ))

#输出operation
y = tf.matmul(x,w1)

#损失函数跟反向传播方法
loss_mse = tf.reduce_mean(tf.square(y_-y))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)

def train_neural(train_step):
    #开始会话,训练
    with tf.Session() as sess:
        init_op = tf.global_variables_initializer()
        sess.run(init_op)
        steps = 20000
        for i in range(steps): #循环20000次
            start = (i*batch_size)%32                      #0 8
            end = (i*batch_size)%32 + batch_size           #8 16
            sess.run(train_step, feed_dict={x:X[start:end], y_:Y_[start:end]})

            if 0:
                if i%500 == 0:
                    print("After %d training steps, w1 is: " % (i))
                    print(sess.run(w1), "\n")
        print("Final w1 is: \n", sess.run(w1))
        
train_neural(train_step)

start
Final w1 is: 
 [[0.98019385]
 [1.0159807 ]]

自定义损失函数

loss = ∑nf(y_,-y)

f(y_,y) =

(1) profit*(y_-y) y<y_ 这里有利益了,profit就是利益率

(2) cost * (y-y_) y>=y_ 这里赔本,成本率

# 假设酸奶成本为9元，利润为1元
cost=9
profit=1

loss = tf.reduce_sum(tf.where(tf.greater(y,y_),cost*(y-y_), profit*(y_-y)))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss) #传入函数
#开始会话,训练

train_neural(train_step)

Final w1 is: 
 [[0.9661967 ]
 [0.97694933]]

来源：https://blog.csdn.net/qq_32460819/article/details/102750395