1、同胚
如果一个映射是一对一的映射、又是满映射,并且是连续的,我们称这个映射为同胚。
2、拓扑共轭
设f:A->A及g:B->B为两个映射,如果存在一同胚h:A->B ,使得h°f=g°h,则称f和g是拓扑共轭的。
3、混沌的概念
是一度量空间,X,Vf:V→V
上是混沌的:
(1)∈N∈>0,有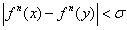
(2) 。
。
(3)fTV∈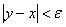 成立。
成立。
 在[-1,1]是混沌的。
在[-1,1]是混沌的。
Step1:先证明 是混沌的。
是混沌的。
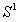 表示平面上单位圆。我们用角表示
表示平面上单位圆。我们用角表示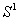 上的点,其
上的点,其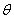 用标准的方法并以弧度为单位进行测量。
用标准的方法并以弧度为单位进行测量。
(1)敏感依赖性
 是
是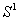 上的映射,对
上的映射,对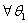 、
、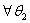
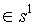 ,有
,有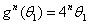 、
、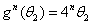

 具有对初始条件的敏感依赖性。
具有对初始条件的敏感依赖性。
(2)拓扑传递
 是
是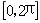 的两个开区间,
的两个开区间, 是对应在
是对应在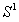 上面的开弧。因为
上面的开弧。因为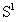 上面的任何小弧都可由某一
上面的任何小弧都可由某一 (n是正整数)最终扩展以覆盖
(n是正整数)最终扩展以覆盖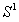 上面任何弧。所以有
上面任何弧。所以有 ,据此推出
,据此推出 。
。
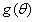 是拓扑传递的。
是拓扑传递的。
(3)周期点在V中稠密,V是一个度量空间。
 ,所以
,所以 是
是 周期点当且仅当
周期点当且仅当 ,
,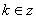 .即当且仅当
.即当且仅当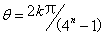 ,且
,且
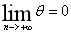 ,证明其周期点是有极限的。
,证明其周期点是有极限的。
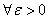 ,必然
,必然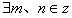 ,使得
,使得 ,所以
,所以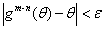 ,
,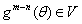 ,
, 是周期点。
是周期点。
 在V中是稠密的。
在V中是稠密的。
 是混沌的。
是混沌的。
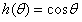 ,h:[0,2π]--->[-1,1]是一对一满射的,并且在[0,2π]是连续的,故h是一个同胚映射。
,h:[0,2π]--->[-1,1]是一对一满射的,并且在[0,2π]是连续的,故h是一个同胚映射。

所以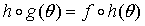
故f、g是拓扑共轭的,他们的动力性态完全等价。
所以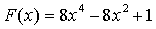 是混沌的。
是混沌的。