题目描述

UNIX系统下有一个行编辑器ed，它每次只对一行文本做删除一个字符、插入一个字符或替换一个字符三种操作。例如某一行的内容是“ABC”，经过把第二个字符替换成“D”、删除第一个字符、末尾插入一个字符“B”，这三步操作后，内容就变成了“DCB”。即“ABC”变成“DCB”需要经过3步操作，我们称它们的编辑距离为3。
现在给你两个任意字符串（不包含空格），请帮忙计算它们的最短编辑距离。

输入描述:
输入包含多组数据。

每组数据包含两个字符串m和n，它们仅包含字母，并且长度不超过1024。

输出描述:
对应每组输入，输出最短编辑距离。
示例1
输入
ABC CBCD
ABC DCB
输出
2
3

分析:

假设序列S和T的长度分别为m和n, 两者的编辑距离表示为 $dp[m][n]$ . 则对序列进行操作时存在以下几种情况:

a, 当S和T的末尾字符相等时, 对末尾字符不需要进行上述定义操作中(亦即"编辑")的任何一个, 也就是不需要增加计数. 则满足条件: $dp[m][n] = dp[m - 1][n - 1]$ .
b, 当S和T的末尾字符不相等时, 则需要对两者之一的末尾进行编辑, 相应的计数会增加1.
- b1, 对S或T的末尾进行修改, 以使之与T或S相等, 则此时 $dp[m][n] = dp[m - 1][n - 1] + 1$ ;
- b2, 删除S末尾的元素, 使S与T相等, 则此时 $dp[m][n] = dp[m - 1][n] + 1$ ;
- b3, 删除T末尾的元素, 使T与S相等, 则此时 $dp[m][n] = dp[m][n - 1] + 1$ ;
- b4, 在S的末尾添加T的尾元素, 使S和T相等, 则此时S的长度变为m+1, 但是此时S和T的末尾元素已经相等, 只需要比较S的前m个元素与T的前n-1个元素, 所以满足 $dp[m][n] = dp[m][n - 1] + 1$ ;
- b5, 在T的末尾添加S的尾元素, 使T和S相等, 此时的情况跟b4相同, 满足 $dp[m][n] = dp[m - 1][n] + 1$ ;
c, 比较特殊的情况是, 当S为空时, $dp[0][n] = n$ ; 而当T为空时, $dp[m][0] = m$ ; 这个很好理解, 例如对于序列"“和"abc”, 则两者的最少操作为3, 即序列""进行3次插入操作, 或者序列"abc"进行3次删除操作.

所以, 编辑距离的动态规划方程为: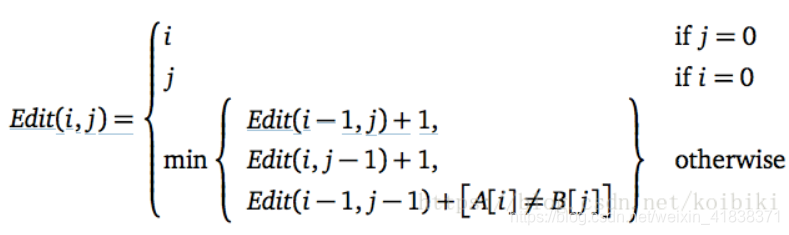

或者：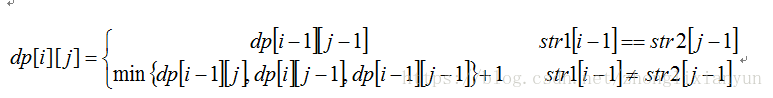

算法计算步骤：

1.对于字符串A ‘jarrry’和字符串B’jerr’，先初始化矩阵dp为 $[len(A) + 1][len(B) + 1]$ ，dp 矩阵的第一行与第一列均从零开始递增，最后得矩阵为

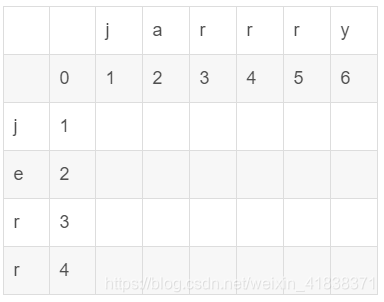
2.然后从第一列开始循环。对于每个矩阵坐标（i，j），设置中间变量temp，

当 A[i] == B[j] 时，temp = 1；否则 temp = 0。

$dp[i][j] = min（dp[i-1][j-1] + temp ，min(dp[i-1][j] + 1 , dp[i][j-1] + 1））$

3.循环完成dp矩阵为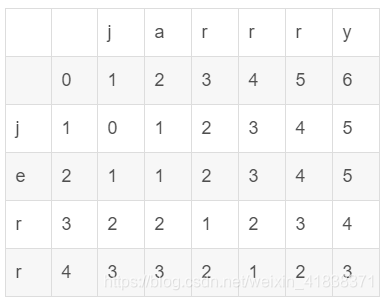

$dp[len(A)][len(B)]$ 就是A,B两个字符串得编辑距离
注意：分配保存结果的空间时，需要指定等于字符串长度+1的空间。

O(m*n) space

def edit_distance(word1, word2):     len1 = len(word1)     len2 = len(word2)     # 分配存储空间     dp = np.zeros((len1 + 1,len2 + 1))     # 初始化第一行和第一列     for i in range(len1 + 1):         dp[i][0] = i;          for j in range(len2 + 1):         dp[0][j] = j;     # 遍历矩阵中的每一个元素，按照动态规划方程来更新     for i in range(1, len1 + 1):         for j in range(1, len2 + 1):             delta = 0 if word1[i-1] == word2[j-1] else 1             dp[i][j] = min(dp[i - 1][j - 1] + delta, min(dp[i-1][j] + 1, dp[i][j - 1] + 1))     return dp[len1][len2]