版权声明:本文博主原创,转载时候请注明。 https://blog.csdn.net/u012336460/article/details/83959457
Ŀ¼
二分查找(查找有序数列中的某个值)
(05,13,19,21,37,56,64,75,80,88,92) 1 2 3 4 5 6 7 8 9 10 12 二分查找算法分析

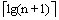
代码:binary_research()
#include <iostream> using namespace std; const int N =10; int a[12]={0 ,5, 13,19, 21,37,56,64,75,80,88,92}; int my_research(int L, int R, int key){ int first = L, last = R-1; while(first < last){ int middle = (first+last)/2; if( a[middle]==key) return middle; else if( a[middle] < key ) first = middle+1; //这里要注意,不能是middle 若果是middle,[middle, last] 可能与[fist, last]区间一样,将发生死循环 else last=middle; } return -1; } int main() { cout << my_research(1, 12,44); return 0; } 二分法的注意事项:
(05,13,19,21,37,56,64,75,80,88,92) 1 2 3 4 5 6 7 8 9 10 12 如果要查找有序数组里面的元素V, 然而数组里面有多个元素都是V。
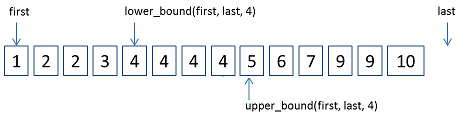
当V存在时,返回出现的第一个位置。 若果不存在,则返回一个这样的下标: 在此处插入V,序列依然有序
#include <iostream> using namespace std; const int N =10; int a[12]={0 ,5, 13,21, 21,21,21,64,75,80,88,92}; int my_lower_bound(int L, int R, int key){ int first = L, last = R-1; while(first < last){ int middle = (first+last)/2; if( a[middle] >= key ) last = middle; else first = middle+1; } return first; } int main() { cout << my_research(1, 12,21); return 0; } 当V存在时,返回出现的最后一个位置的下一个位置。若果不存在,则返回一个这样的下标: 在此处插入V,序列依然有序
#include <iostream> using namespace std; const int N =10; int a[12]={0 ,5, 13,21, 21,21,21,64,75,80,88,92}; int my_upper_bound(int L, int R, int key){ int first = L, last = R-1; while(first < last){ int middle = (first+last)/2; if( a[middle] <= key ) first = middle+1; else last = middle; } return first; } int main() { cout << my_research(1, 12,21); return 0; } 实数区域上的二分
while(L+ esp < R){ double mid = (L + R) /2 if ( ) R = middle else L = middle } 或者干脆采用循环固定次数的方法,也是不错的策略
for(int i=0;i<100;i++){ double middle = (L+R) /2; if() L=middle; else R =middle } 二分答案(不只是查找值)
题目描述中若出现类似: “最大值最小”的含义,这个答案就具有单调性,可用二分答案法。
这个宏观的最优化问题,可以抽象为一个函数,其“定义域”是该问题的可行方案。
https://www.luogu.org/problemnew/show/P1577
最大化最小值:POJ 2456
最大化平均值:
文章来源: 二分查找