整个项目都托管在了 Github 上:https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp
查找更为方便的版本见:https://alg4.ikesnowy.com/
这一节内容可能会用到的库文件有 PriorityQueue,同样在 Github 上可以找到。
善用 Ctrl + F 查找题目。
2.4.1
用序列 P R I O * R * * I * T * Y * * * Q U E * * * U * E
(字母表示插入元素,星号表示删除最大元素)
操作一个初始为空的优先队列。
给出每次删除最大元素返回的字符。
R R P O T Y I I U Q E U
优先队列的变化如下:
| 输入命令 | 优先队列 | 输出 |
|---|---|---|
| P | P | |
| R | P R | |
| I | P R I | |
| O | P R I O | |
| * | P I O | R |
| R | P I O R | |
| * | P I O | R |
| * | I O | P |
| I | I O I | |
| * | I I | O |
| T | I I T | |
| * | I I | T |
| Y | I I Y | |
| * | I I | Y |
| * | I | I |
| * | I | |
| Q | Q | |
| U | Q U | |
| E | Q U E | |
| * | Q E | U |
| * | E | Q |
| * | E | |
| U | U | |
| * | U | |
| E | E |
2.4.2
分析以下说法:
要实现在常数时间找到最大元素,
为何不用一个栈或者队列,
然后记录已插入的最大元素并在找出最大元素时返回它的值。
这种方式只能取出一次最大值,这个最大值就是输入序列里面的最大值。
当需要继续取出最大值时(即继续取第二大、第三大、第 i 大的元素),
这个方法就不再适用了(或者说不能在常数时间内完成)。
2.4.3
用以下数据结构实现优先队列,支持插入元素和删除最大元素操作:
无序数组、有序数组、无序链表和链表。
将你的 4 种实现中每种操作在最坏情况下的运行时间上下限制成一张表格。
有序数组的官方版本:https://algs4.cs.princeton.edu/24pq/OrderedArrayMaxPQ.java.html
无序数组的官方版本:https://algs4.cs.princeton.edu/24pq/UnorderedArrayMaxPQ.java.html
| 实现 | insert() | delMax() |
|---|---|---|
| 有序数组 | N | 1 |
| 有序链表 | N | 1 |
| 无序数组 | 1 | N |
| 无序链表 | 1 | N |
在库文件中定义了如下接口,所有的(最大)优先队列都会实现它。
using System; namespace PriorityQueue { /// <summary> /// 实现优先队列 API 的接口。 /// </summary> /// <typeparam name="Key">优先队列容纳的元素。</typeparam> public interface IMaxPQ<Key> where Key : IComparable<Key> { /// <summary> /// 向优先队列中插入一个元素。 /// </summary> /// <param name="v">插入元素的类型。</param> void Insert(Key v); /// <summary> /// 返回最大元素。 /// </summary> /// <returns></returns> Key Max(); /// <summary> /// 删除并返回最大元素。 /// </summary> /// <returns></returns> Key DelMax(); /// <summary> /// 返回队列是否为空。 /// </summary> /// <returns></returns> bool IsEmpty(); /// <summary> /// 返回队列中的元素个数。 /// </summary> /// <returns></returns> int Size(); } } 于是我们就可以使用这样的方法测试所有类型的优先队列:
static void test(IMaxPQ<string> pq) { Console.WriteLine(pq.ToString()); pq.Insert("this"); pq.Insert("is"); pq.Insert("a"); pq.Insert("test"); while (!pq.IsEmpty()) Console.Write(pq.DelMax() + " "); Console.WriteLine(); } 给出链表的实现,基于数组的实现可以点击「另请参阅」中的 PriorityQueue 库查看。
无序链表
using System; namespace PriorityQueue { /// <summary> /// 不保持元素输入顺序的优先队列。(基于链表) /// </summary> /// <typeparam name="Key">优先队列中的元素类型。</typeparam> public class UnorderedLinkedMaxPQ<Key> : IMaxPQ<Key> where Key : IComparable<Key> { /// <summary> /// 保存元素的链表。 /// </summary> private readonly LinkedList<Key> pq; /// <summary> /// 默认构造函数,建立一条优先队列。 /// </summary> public UnorderedLinkedMaxPQ() { this.pq = new LinkedList<Key>(); } /// <summary> /// 获得(但不删除)优先队列中的最大元素。 /// </summary> /// <returns></returns> public Key Max() { int max = 0; for (int i = 1; i < this.pq.Size(); i++) if (Less(this.pq.Find(max), this.pq.Find(i))) max = i; return this.pq.Find(max); } /// <summary> /// 返回并删除优先队列中的最大值。 /// </summary> /// <returns></returns> public Key DelMax() { int max = 0; for (int i = 1; i < this.pq.Size(); i++) if (Less(this.pq.Find(max), this.pq.Find(i))) max = i; return this.pq.Delete(max); } /// <summary> /// 向优先队列中插入一个元素。 /// </summary> /// <param name="v">需要插入的元素。</param> public void Insert(Key v) => this.pq.Insert(v); /// <summary> /// 检查优先队列是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.pq.IsEmpty(); /// <summary> /// 检查优先队列中含有的元素数量。 /// </summary> /// <returns></returns> public int Size() => this.pq.Size(); /// <summary> /// 比较第一个元素是否小于第二个元素。 /// </summary> /// <param name="a">第一个元素。</param> /// <param name="b">第二个元素。</param> /// <returns></returns> private bool Less(Key a, Key b) => a.CompareTo(b) < 0; } } 有序链表
using System; namespace PriorityQueue { /// <summary> /// 元素保持输入顺序的优先队列。(基于链表) /// </summary> /// <typeparam name="Key">优先队列中的元素类型。</typeparam> public class OrderedLinkedMaxPQ<Key> : IMaxPQ<Key> where Key : IComparable<Key> { /// <summary> /// 用于保存元素的链表。 /// </summary> private readonly LinkedList<Key> pq; /// <summary> /// 默认构造函数,建立一条优先队列。 /// </summary> public OrderedLinkedMaxPQ() { this.pq = new LinkedList<Key>(); } /// <summary> /// 向优先队列中插入一个元素。 /// </summary> /// <param name="v">需要插入的元素。</param> public void Insert(Key v) { int i = this.pq.Size() - 1; while (i >= 0 && Less(v, this.pq.Find(i))) i--; this.pq.Insert(v, i + 1); } /// <summary> /// 返回并删除优先队列中的最大值。 /// </summary> /// <returns></returns> public Key DelMax() => this.pq.Delete(this.pq.Size() - 1); /// <summary> /// 检查优先队列是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.pq.IsEmpty(); /// <summary> /// 获得(但不删除)优先队列中的最大元素。 /// </summary> /// <returns></returns> public Key Max() => this.pq.Find(this.pq.Size() - 1); /// <summary> /// 检查优先队列中含有的元素数量。 /// </summary> /// <returns></returns> public int Size() => this.pq.Size(); /// <summary> /// 比较第一个元素是否小于第二个元素。 /// </summary> /// <param name="a">第一个元素。</param> /// <param name="b">第二个元素。</param> /// <returns></returns> private bool Less(Key a, Key b) => a.CompareTo(b) < 0; } } 2.4.4
一个按降序排列的数组也是一个面向最大元素的堆吗?
是的。
例如这个数组:9 8 7 6 5,画成二叉堆如下:

2.4.5
将 E A S Y Q U E S T I O N 顺序插入一个面向最大元素的堆中,给出结果。

2.4.6
按照练习 2.4.1 的规则,
用序列 P R I O * R * * I * T * Y * * * Q U E * * * U * E 操作一个初始空间为空的面向最大元素的堆,
给出每次操作后堆的内容。
官方给出的最大堆实现:https://algs4.cs.princeton.edu/24pq/MaxPQ.java.html
运行示意图:
运行结果:
P R P R P I R P O I P O I R P O I P O I O I O I I I I T I I I I Y I I I I I Q U Q U Q E Q E E U E
最大堆的实现
using System; using System.Collections; using System.Collections.Generic; namespace PriorityQueue { /// <summary> /// 最大堆。(数组实现) /// </summary> /// <typeparam name="Key">最大堆中保存的元素。</typeparam> public class MaxPQ<Key> : IMaxPQ<Key>, IEnumerable<Key> where Key : IComparable<Key> { private Key[] pq; // 保存元素的数组。 private int n; // 堆中的元素数量。 /// <summary> /// 默认构造函数。 /// </summary> public MaxPQ() : this(1) { } /// <summary> /// 建立指定容量的最大堆。 /// </summary> /// <param name="capacity">最大堆的容量。</param> public MaxPQ(int capacity) { this.pq = new Key[capacity]; this.n = 0; } /// <summary> /// 删除并返回最大元素。 /// </summary> /// <returns></returns> public Key DelMax() { if (IsEmpty()) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); Key max = this.pq[1]; Exch(1, this.n--); Sink(1); this.pq[this.n + 1] = default(Key); if ((this.n > 0) && (this.n == this.pq.Length / 4)) Resize(this.pq.Length / 2); return max; } /// <summary> /// 向堆中插入一个元素。 /// </summary> /// <param name="v">需要插入的元素。</param> public void Insert(Key v) { if (this.n == this.pq.Length - 1) Resize(2 * this.pq.Length); this.pq[++this.n] = v; Swim(this.n); } /// <summary> /// 检查堆是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.n == 0; /// <summary> /// 获得堆中最大元素。 /// </summary> /// <returns></returns> public Key Max() => this.pq[1]; /// <summary> /// 获得堆中元素的数量。 /// </summary> /// <returns></returns> public int Size() => this.n; /// <summary> /// 获取堆的迭代器,元素以降序排列。 /// </summary> /// <returns></returns> public IEnumerator<Key> GetEnumerator() { MaxPQ<Key> copy = new MaxPQ<Key>(this.n); for (int i = 1; i <= this.n; i++) copy.Insert(this.pq[i]); while (!copy.IsEmpty()) yield return copy.DelMax(); // 下次迭代的时候从这里继续执行。 } /// <summary> /// 获取堆的迭代器,元素以降序排列。 /// </summary> /// <returns></returns> IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } /// <summary> /// 使元素上浮。 /// </summary> /// <param name="k">需要上浮的元素。</param> private void Swim(int k) { while (k > 1 && Less(k / 2, k)) { Exch(k, k / 2); k /= 2; } } /// <summary> /// 使元素下沉。 /// </summary> /// <param name="k">需要下沉的元素。</param> private void Sink(int k) { while (k * 2 <= this.n) { int j = 2 * k; if (j < this.n && Less(j, j + 1)) j++; if (!Less(k, j)) break; Exch(k, j); k = j; } } /// <summary> /// 重新调整堆的大小。 /// </summary> /// <param name="capacity">调整后的堆大小。</param> private void Resize(int capacity) { Key[] temp = new Key[capacity]; for (int i = 1; i <= this.n; i++) { temp[i] = this.pq[i]; } this.pq = temp; } /// <summary> /// 判断堆中某个元素是否小于另一元素。 /// </summary> /// <param name="i">判断是否较小的元素。</param> /// <param name="j">判断是否较大的元素。</param> /// <returns></returns> private bool Less(int i, int j) => this.pq[i].CompareTo(this.pq[j]) < 0; /// <summary> /// 交换堆中的两个元素。 /// </summary> /// <param name="i">要交换的第一个元素下标。</param> /// <param name="j">要交换的第二个元素下标。</param> private void Exch(int i, int j) { Key swap = this.pq[i]; this.pq[i] = this.pq[j]; this.pq[j] = swap; } /// <summary> /// 检查当前二叉树是不是一个最大堆。 /// </summary> /// <returns></returns> private bool IsMaxHeap() => IsMaxHeap(1); /// <summary> /// 确定以 k 为根节点的二叉树是不是一个最大堆。 /// </summary> /// <param name="k">需要检查的二叉树根节点。</param> /// <returns></returns> private bool IsMaxHeap(int k) { if (k > this.n) return true; int left = 2 * k; int right = 2 * k + 1; if (left <= this.n && Less(k, left)) return false; if (right <= this.n && Less(k, right)) return false; return IsMaxHeap(left) && IsMaxHeap(right); } } } 2.4.7
在堆中,最大的元素一定在位置 1 上,第二大的元素一定在位置 2 或者 3 上。
对于一个大小为 31 的堆,
给出第 k 大的元素可能出现的位置和不可能出现的位置,
其中 k=2、3、4(设元素值不重复)。
k = 2 时,
只可能出现在位置 2、3 上(根节点的子结点,深度为 2,根节点深度为 1)
k = 3 时,
可以直接是根节点的子结点(第 2 或第 3 位,深度为 2),
也可以是第二大元素的子结点(第 4~7 位,也就是深度为 3 的所有位置)
k = 4 时,
可以直接是根节点的子结点(深度为 2 的点)
也可以是第二大元素的子结点(深度为 3 的点)
也可以是第三大元素的子结点(深度为 4 的点)
故范围为第 2~15 位。
不难看出第 k 大元素只可能出现在深度<k 的位置(\(k \ge 2\))
即位置小于 \(2 ^ k - 1, (k \ge 2)\)
2.4.8
回答上一道练习中第 k 小元素的可能和不可能的位置。
不难看出第 k 大元素只可能出现在深度<k 的位置(\(k \ge 2\))
即位置小于 \(2^k - 1, (k \ge 2)\)。
出现范围为 \([2, \min \{2^k -1, n\}]\),其中 n 为堆的大小。
2.4.9
给出 A B C D E 五个元素可能构造出来的所有堆,
然后给出 A A A B B 这五个元素可能构造出来的所有堆。
首先 A B C D E 中,根节点必须是 E (假设为最大堆)
D 只能选择 E 作为父结点。
C 可以选择 D 或者 E 作为父结点。
B 可以选择 C 或 D 或 E 作为父结点。
A 可以选择 B 或 C 或 D 或 E 作为父结点。
又由于堆的大小为 5,堆的结构固定,一共三层。
E 只能为根节点
D 可以在左侧或者右侧
当 D 在左侧时,
D 的子结点可以在 A B C 中任取两个,剩下一个当 E 的右侧子结点
总共有 A(3, 2) = 6 种
当 D 在右侧时,
C 的子结点只能取 A 和 B ,故只有 A(2, 2) = 2 种情况。
综上,最大堆总共有 6 + 2 = 8 种构造堆的方式。
最小堆的构造同理,也有 8 种构造方式。
故总共有 8 + 8 = 16 种构造方式。
构造方式(最大堆):

最大堆
B 只能作为 B 的子结点,A 可以是 B 或 A 的子结点。
根节点恒为 B
第二层结点有两种选择 A B 和 B A
第三层只有一种选择 A A
故总共有两种构造堆的方式。
最小堆
根节点恒为 A
第二层可以是 A A 或 A B
第二层是 A A 时
第三层只能选择 B B
第二层时 A B 时
第三层可选择 A B 或 B A
故总共有三种构造堆的方式。
综上所述,总共有 2 + 3 = 5 种构造方式。
构造方式(全部):

2.4.10
假设我们不想浪费堆排序的数组 pq[] 中的那个位置,
将最大元素放在 pq[0],它的子结点放在 pq[1] 和 pq[2],以此类推。
pq[k] 的父结点和子结点在哪里?
左子树位于 \(2k+1\),右子树位于 \(2k+2\),父结点位于 \(\lfloor (i-1)/2 \rfloor\) 。
2.4.11
如果你的应用中有大量插入元素的操作,但只有若干删除最大元素的操作,
哪种优先队列的实现方法更有效:堆、无序数组、有序数组?
有大量插入操作,选择插入操作为常数级别的无序数组实现较为合适。
2.4.12
如果你的应用场景中大量的找出最大元素的操作,但插入元素和删除最大元素操作相对较少,
哪种优先队列的实现方法更有效:堆、无序数组、有序数组?
有序数组,查找最大元素操作是 O(1) 的。
堆要看具体实现,基于数组的实现和有序数组类似,
在插入操作较多的情况下甚至会优于有序数组。
注:
官网给出的堆实现会在插入/删除操作之后对整个数组进行检查,
确认是否为最大堆(isMaxHeap 方法)。
在测试时务必删除这部分代码。
2.4.13
想办法在 sink() 中避免检查 j<N。
在官方实现的基础上直接删除 j<N 语句,随后在 DelMax() 方法中在 sink(1) 之前让 pq[n + 1] = pq[1] 即可。
首先保存最大值,然后把堆中的第一个元素和最后一个元素交换,随后使 n = n - 1。
随后让 pq[n + 1] = pq[1],这样在下沉操作时就不会下沉到 pq[n + 1]了。(相等的元素是不会交换的)
故之后的 Sink() 语句中不再需要进行边界判断,直接删去即可。
修改后 DelMax() 的代码如下:
public Key DelMax() { if (IsEmpty()) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); Key max = this.pq[1]; Exch(1, this.n--); pq[n + 1] = pq[1]; Sink(1); this.pq[this.n + 1] = default(Key); if ((this.n > 0) && (this.n == this.pq.Length / 4)) Resize(this.pq.Length / 2); Debug.Assert(IsMaxHeap()); return max; } 2.4.14
对于没有重复元素的大小为 N 的堆,一次删除最大元素的操作中最少要交换几个元素?
构造一个能够达到这个交换次数的大小为 15 的堆。
连续两次删除最大元素呢?三次呢?
对于 n <= 2 的堆
第一步让最大元素和末端元素交换。
第二步下沉时由于 n <= 1,不需要交换。
故总共发生了一次交换,两个元素发生了交换。
对于 n = 3 的堆
第一步让最大元素和末端元素交换。
第二步如果末端元素大于另一侧的子结点,那么就不需要交换。
故最优情况时总共发生一次交换,两个元素被交换。
对于 n > 3 的堆。
第一步需要让最末端元素和最大元素交换。
由于堆中第二大的元素必定位于根节点之后。
故最末端元素一定小于该第二大元素。
因此在下沉操作时必定会和第二大元素进行交换。
故至少发生两次交换,总共有三个元素发生了交换。
构造的堆(n=15)

92 和 100 交换,随后 92 和 99 交换
构造最优情况堆的方式如下(取根结点为 100):

对于每个结点,左子结点大于右子结点,
且左子结点的子元素都小于右子树的最小值,
(上例中省略了这部分元素,可以将它们当作负数)
于是第一次 DelMax 的时候,只需要两次交换,三个元素被交换。
(即 87 最后被交换到上例中 99 的位置)
第二次 DelMax 的时候,只需要三次交换,六个元素被交换.
(88 交换到 97 的位置)
因此当 n > 7 时,连续两次 DelMax() 最少只需要 5 次交换。
第三次 DelMax 的时候,只需要四次交换,九个元素被交换。
(89 交换到 95 的位置)
因此当 n > 15 时,连续三次 DelMax() 最少只需要 9 次交换。
2.4.15
设计一个程序,在线性时间内检测数组 pq[] 是否是一个面向最小元素的堆。
MinPQ 的官方实现见:https://algs4.cs.princeton.edu/24pq/MinPQ.java.html
事实上只需要把 MaxPQ 中的比较调换方向即可。
在线性时间内检测是否是面向最小元素的堆的方法:
/// <summary> /// 确定以 k 为根节点的二叉树是不是一个最小堆。 /// </summary> /// <param name="k">需要检查的二叉树根节点。</param> /// <returns></returns> private bool IsMinHeap(int k) { if (k > this.n) return true; int left = 2 * k; int right = 2 * k + 1; if (left <= this.n && Greater(k, left)) return false; if (right <= this.n && Greater(k, right)) return false; return IsMinHeap(left) && IsMinHeap(right); } 用递归方法遍历整个二叉树,确认都满足堆的性质。由于每个结点都只会被比较三次(与父结点比较一次,与每个子结点各比较一次),由于 3N~N,因此这个方法是 O(n) 的。
最小堆的接口 IMinPQ。
using System; namespace PriorityQueue { /// <summary> /// 实现优先队列 API 的接口。(最小堆) /// </summary> /// <typeparam name="Key">优先队列容纳的元素。</typeparam> public interface IMinPQ<Key> where Key : IComparable<Key> { /// <summary> /// 向优先队列中插入一个元素。 /// </summary> /// <param name="v">插入元素的类型。</param> void Insert(Key v); /// <summary> /// 返回最小元素。 /// </summary> /// <returns></returns> Key Min(); /// <summary> /// 删除并返回最小元素。 /// </summary> /// <returns></returns> Key DelMin(); /// <summary> /// 返回队列是否为空。 /// </summary> /// <returns></returns> bool IsEmpty(); /// <summary> /// 返回队列中的元素个数。 /// </summary> /// <returns></returns> int Size(); } } MinPQ.cs
using System; using System.Collections; using System.Collections.Generic; using System.Diagnostics; namespace PriorityQueue { /// <summary> /// 最小堆。(数组实现) /// </summary> /// <typeparam name="Key">最小堆中保存的元素类型。</typeparam> public class MinPQ<Key> : IMinPQ<Key>, IEnumerable<Key> where Key : IComparable<Key> { private Key[] pq; // 保存元素的数组。 private int n; // 堆中的元素数量。 /// <summary> /// 默认构造函数。 /// </summary> public MinPQ() : this(1) { } /// <summary> /// 建立指定容量的最小堆。 /// </summary> /// <param name="capacity">最小堆的容量。</param> public MinPQ(int capacity) { this.pq = new Key[capacity + 1]; this.n = 0; } /// <summary> /// 从已有元素建立一个最小堆。(O(n)) /// </summary> /// <param name="keys">已有元素。</param> public MinPQ(Key[] keys) { this.n = keys.Length; this.pq = new Key[keys.Length + 1]; for (int i = 0; i < keys.Length; i++) this.pq[i + 1] = keys[i]; for (int k = this.n / 2; k >= 1; k--) Sink(k); Debug.Assert(IsMinHeap()); } /// <summary> /// 删除并返回最小元素。 /// </summary> /// <returns></returns> public Key DelMin() { if (IsEmpty()) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); Key min = this.pq[1]; Exch(1, this.n--); this.pq[this.n + 1] = this.pq[1]; Sink(1); this.pq[this.n + 1] = default(Key); if ((this.n > 0) && (this.n == this.pq.Length / 4)) Resize(this.pq.Length / 2); //Debug.Assert(IsMinHeap()); return min; } /// <summary> /// 向堆中插入一个元素。 /// </summary> /// <param name="v">需要插入的元素。</param> public void Insert(Key v) { if (this.n == this.pq.Length - 1) Resize(2 * this.pq.Length); this.pq[++this.n] = v; Swim(this.n); //Debug.Assert(IsMinHeap()); } /// <summary> /// 检查堆是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.n == 0; /// <summary> /// 获得堆中最小元素。 /// </summary> /// <returns></returns> public Key Min() => this.pq[1]; /// <summary> /// 获得堆中元素的数量。 /// </summary> /// <returns></returns> public int Size() => this.n; /// <summary> /// 获取堆的迭代器,元素以降序排列。 /// </summary> /// <returns></returns> public IEnumerator<Key> GetEnumerator() { MaxPQ<Key> copy = new MaxPQ<Key>(this.n); for (int i = 1; i <= this.n; i++) copy.Insert(this.pq[i]); while (!copy.IsEmpty()) yield return copy.DelMax(); // 下次迭代的时候从这里继续执行。 } /// <summary> /// 获取堆的迭代器,元素以降序排列。 /// </summary> /// <returns></returns> IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } /// <summary> /// 使元素上浮。 /// </summary> /// <param name="k">需要上浮的元素。</param> private void Swim(int k) { while (k > 1 && Greater(k / 2, k)) { Exch(k, k / 2); k /= 2; } } /// <summary> /// 使元素下沉。 /// </summary> /// <param name="k">需要下沉的元素。</param> private void Sink(int k) { while (k * 2 <= this.n) { int j = 2 * k; if (Greater(j, j + 1)) j++; if (!Greater(k, j)) break; Exch(k, j); k = j; } } /// <summary> /// 重新调整堆的大小。 /// </summary> /// <param name="capacity">调整后的堆大小。</param> private void Resize(int capacity) { Key[] temp = new Key[capacity]; for (int i = 1; i <= this.n; i++) { temp[i] = this.pq[i]; } this.pq = temp; } /// <summary> /// 判断堆中某个元素是否大于另一元素。 /// </summary> /// <param name="i">判断是否较大的元素。</param> /// <param name="j">判断是否较小的元素。</param> /// <returns></returns> private bool Greater(int i, int j) => this.pq[i].CompareTo(this.pq[j]) > 0; /// <summary> /// 交换堆中的两个元素。 /// </summary> /// <param name="i">要交换的第一个元素下标。</param> /// <param name="j">要交换的第二个元素下标。</param> private void Exch(int i, int j) { Key swap = this.pq[i]; this.pq[i] = this.pq[j]; this.pq[j] = swap; } /// <summary> /// 检查当前二叉树是不是一个最小堆。 /// </summary> /// <returns></returns> private bool IsMinHeap() => IsMinHeap(1); /// <summary> /// 确定以 k 为根节点的二叉树是不是一个最小堆。 /// </summary> /// <param name="k">需要检查的二叉树根节点。</param> /// <returns></returns> private bool IsMinHeap(int k) { if (k > this.n) return true; int left = 2 * k; int right = 2 * k + 1; if (left <= this.n && Greater(k, left)) return false; if (right <= this.n && Greater(k, right)) return false; return IsMinHeap(left) && IsMinHeap(right); } } } 2.4.16
对于 N=32,构造数组使得堆排序使用的比较次数最多以及最少。
最好情况比较简单,只需要一个所有键值完全相同的数组即可。
最坏情况的构造方法参考了一篇论文(见「另请参阅」部分),结果如下:

最好输入:1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
最坏输入:1 4 7 12 10 16 14 19 17 20 5 27 8 28 2 24 9 18 6 23 11 22 21 31 13 26 25 30 15 29 3 32
用于构造堆排序最坏情况的类。
using System; using System.Collections; using System.Collections.Generic; using System.Diagnostics; namespace PriorityQueue { /// <summary> /// 生成最大堆的最坏情况。参考论文:https://arxiv.org/abs/1504.01459 /// </summary> public class MaxPQWorstCase { private int[] pq; // 保存元素的数组。 private int n; // 堆中的元素数量。 /// <summary> /// 建立指定容量的最大堆。 /// </summary> /// <param name="capacity">最大堆的容量。</param> public MaxPQWorstCase(int capacity) { this.pq = new int[capacity + 1]; this.n = 0; } /// <summary> /// 制造堆排序的最坏情况。 /// </summary> /// <param name="n">需要构造的数组大小。</param> /// <returns>最坏情况的输入数组。</returns> public int[] MakeWorst(int n) { int[] strategy = Win(n); for (int i = 0; i < strategy.Length; i++) { UnRemoveMax(strategy[i]); } for (int i = 1; i <= this.n / 2; i++) UnFixHeap(i); int[] worstCase = new int[n]; for (int i = 1; i <= n; i++) worstCase[i - 1] = this.pq[i]; return worstCase; } private bool Less(int i, int j) => this.pq[i].CompareTo(this.pq[j]) < 0; private int PullDown(int i, int j) { int toReturn = this.pq[j]; for (int m = j; m / 2 >= i; m /= 2) { this.pq[m] = this.pq[m / 2]; } return toReturn; } private void UnFixHeap(int i) { int j = (int)(i * Math.Pow(2, Math.Floor(Math.Log10(this.n / i) / Math.Log10(2)))); this.pq[i] = PullDown(i, j); } private void UnRemoveMax(int i) { int p = (this.n + 1) / 2; if (Less(p, i)) return; this.n++; this.pq[this.n] = PullDown(1, i); this.pq[1] = this.n; } private int[] Par(int l) { int n = (int)Math.Pow(2, l) - 1; int[] s7 = { 0, 1, 2, 3, 4, 4, 5 }; int[] strategy = new int[n]; for (int i = 0; i < Math.Min(n, 7); i++) { strategy[i] = s7[i]; } if (n <= 7) return strategy; for (int lev = 3; lev < l; lev++) { int i = (int)Math.Pow(2, lev) - 1; strategy[i] = i; strategy[i + 1] = i - 1; strategy[i + 2] = i + 1; strategy[i + 3] = i + 2; strategy[i + 4] = i + 4; strategy[i + 5] = i + 3; for (int k = i + 6; k <= 2 * i; k++) { strategy[k] = k - 1; } } return strategy; } private int[] Win(int n) { int[] strategy = new int[n]; int[] s = Par((int)Math.Floor(Math.Log10(n) / Math.Log10(2)) + 1); for (int i = 1; i <= n - 1; i++) { strategy[i] = s[i]; } int I = (int)Math.Pow(2, Math.Floor(Math.Log10(n + 1) / Math.Log10(2))) - 1; if ((n == I) || (n <= 7)) return strategy; strategy[I] = I; if (n == I + 1) return strategy; strategy[I + 1] = (I + 1) / 2; if (n == I + 2) return strategy; for (int i = I + 2; i <= n - 1; i++) { if (i == 2 * I - 2) strategy[i] = i; else strategy[i] = i - 1; } return strategy; } } } 给出堆排序最坏情况构造方法的论文
Suchenek M A. A Complete Worst-Case Analysis of Heapsort with Experimental Verification of Its Results, A manuscript (MS)[J]. arXiv preprint arXiv:1504.01459, 2015.
本题用到的库文件
PriorityQueue 库
2.4.17
证明:构造大小为 k 的面向对象最小元素的优先队列,
然后进行 N-k 次替换最小元素操作(删除最小元素后再插入元素)后,
N 个元素中的前 k 大元素均会留在优先队列中。
英文版原文是:insert followed by remove the minimum,因此是先插入再删除。
大致上相当于一个缓冲区,把比较大的留下来,比较小的筛出去。
首先我们有一个大小为 k 的优先队列,保证最小值在最前。
接下来我们插入一个元素,可以分成两种情况。
如果插入的元素比最小值还要小,那么这个插入的元素会在之后被删除,原队列中的元素不变。
如果插入的元素比最小值大(或者相等),那么最小值会被删除,留下插入的元素。
于是可以观察到这样一个逻辑,在不断的插入过程中,比较小的元素会被过滤,只留下较大的元素。
那么我们可以把题目转化为:
向一个优先队列插入 N 个元素,保证队列的大小不超过 k,如果超过 k 了就删除最小值。
那么前 k 次插入不受影响,之后的 N-k 次插入就会按照之前说过的流程进行。
最后只留下 N 个元素中较大的 k 个元素,得证。
2.4.18
在 MaxPQ 中,如果一个用例使用 insert() 插入了一个比队列中的所有元素都大的新元素,随后立即调用 delMax()。
假设没有重复元素,此时的堆和进行这些操作之前的堆完全相同吗?
进行两次 insert()
(第一次插入一个比队列所有元素都大的元素,第二次插入一个更大的元素)
操作接两次 delMax() 操作呢?
首先看第一种情况,一次 insert() 接一次 delMax()。
由于插入的数比堆中的所有元素都大,这个元素会一路上升到根结点。
记上升路径上的点为 $ a_1,a_2,a_3, \dots , a_k $,其中 $ a_k $ 是插入的结点,$ a_1 $ 是根结点。
插入完成后路径上点的次序变为 $ a_k, a_1, a_2, \dots, a_{k-1} $ 。
随后进行一次 delMax(),先做交换,次序变为 $ a_{k-1}, a_1, \dots, a_{k-2}, a_k $ 。
由于 $ a_1 $ 是堆中原来的最大值,下沉时一定会和它交换。
根据定义,二叉堆是父结点总是优于子结点的完全二叉树,因此以后续结点作为根结点的子树也都是堆。
故同理 $ a_{k-1} $ 会和 $ a_2, a_3, \dots,a_{k-2} $ 交换,即沿原路径返回。
因此这种情况下前后堆不发生改变。
然后看第二种情况,操作顺序为 insert() insert() delMax() delMax()。
根据之前的结论,插入最大结点之后立即删除最大元素不会使堆发生变化,中间的两个操作抵消。
序列变为:insert() delMax()。
同理再次利用刚才的结论,操作抵消,堆不发生变化。
故第二种情况也不会使堆发生改变。
2.4.19
实现 MaxPQ 的一个构造函数,接受一个数组作为参数。
使用正文 2.4.5.1 节中所述的自底向上的方法构造堆。
官方实现已经包含了这部分的代码,见:https://algs4.cs.princeton.edu/24pq/MaxPQ.java.html
相应的构造函数(Java)
public MaxPQ(Key[] keys) { n = keys.length; pq = (Key[]) new Object[keys.length + 1]; for (int i = 0; i < n; i++) pq[i+1] = keys[i]; for (int k = n/2; k >= 1; k--) sink(k); assert isMaxHeap(); } 构造函数(C#)
/// <summary> /// 从已有元素建立一个最大堆。(O(n)) /// </summary> /// <param name="keys">已有元素。</param> public MaxPQ(Key[] keys) { this.n = keys.Length; this.pq = new Key[keys.Length + 1]; for (int i = 0; i < keys.Length; i++) this.pq[i + 1] = keys[i]; for (int k = this.n / 2; k >= 1; k--) Sink(k); Debug.Assert(IsMaxHeap()); } 2.4.20
证明:基于下沉的堆构造方法使用的比较次数小于 2N,交换次数小于 N。
官网给出了解答:https://algs4.cs.princeton.edu/24pq/
首先介绍第一种解法。
设叶子结点的高度为 $ 0 $,根结点的高度为 $ h $。
于是某个结点 sink 时的最大交换次数即为该结点的高度。
故某一层结点的最大交换次数为 该层结点数 × 该层的高度。
于是总交换次数最大为:
\[ \begin{align*} & h+2(h-1)+2^2(h-2)+ \dots + 2^h(0) \\ & =\sum_{k=0}^{h-1} 2^k(h-k) \\ & =h\sum_{k=0}^{h-1}2^k - \sum_{k=0}^{h-1}k2^k \\ \end {align*} \]
第一项为等比数列的和,第二项为等差数列乘以等比数列的和。
于是第一项可以直接通过公式求得,第二项可以利用错位相减法求得。
\[ \begin{align*} & h\sum_{k=0}^{h-1}2^k - \sum_{k=0}^{h-1}k2^k \\ & =h2^{h}-h-\sum_{k=0}^{h-1}k2^k \\ & =h2^{h}-h +\sum_{k=0}^{h-1} k2^k - 2\sum_{k=0}^{h-1} k2^k \\ & =h2^{h}-h+2^h - 2-(h-1)2^h \\ & =2^{h+1}-h-2 \\ & =N-h-1 \le N \end{align*} \]
于是交换次数小于 $ N $,比较次数小于 $ 2N $。
另一种解法,可以配合官网的图片帮助理解。
首先堆中某个结点最多一路下沉到叶子结点,
最大交换次数就是该结点的高度(记叶子结点的高度为 0)。
考虑根结点一路下沉到叶子结点的轨迹,
设为 $ a_0, a_1, a_2, ... , a_k $,其中 $ k $ 为根结点的高度,$ a_0 $ 是根结点。
$ a_0 $ 下沉后结点顺序变为 $ a_1, a_2, ..., a_k, a_0 $ 。
根据下沉的定义,有 $ a_1 > a_2 > \dots > a_k > a_0 $ 。
因此 $ a_1 $ 下沉时不可能与 $ a_2 $ 交换,而会向另一个方向下沉。
其余结点同理,可以发现每个结点的下沉路径不会与其他结点重合。
一棵完全二叉树共有 $ N - 1 $ 条边,每访问一条边代表进行了一次交换。
故交换次数必定小于 $ N $,比较次数为交换次数的两倍小于 $ 2N $。
2.4.21
基础数据结构。
说明如何使用优先队列实现第一章中的栈、队列和随机队列这几种数据结构。
给元素添上序号组成结点,按照序号排序即可,每个结点可以用类似于这样的实现:
class ElemType<T> : IComparable<ElemType<T>> { private int key; private T element; public ElemType(int key) => this.key = key; public int CompareTo(ElemType<T> other) { return this.key.CompareTo(other.key); } } 栈:
用最大元素在最前的优先队列。
每个结点都包含一个元素和一个序号,
插入新元素时序号递增,这样最后插入的元素总在最前。
队列:
用最小元素在最前的优先队列。
每个结点都包含一个元素和一个序号,
插入新元素时序号递增,这样最先插入的元素总在最前。
随机队列:
优先队列的选择任意
每个结点都包含一个元素和一个序号,
插入新元素时随机指定一个序号,这样元素的顺序就是任意的了。
2.4.22
调整数组大小。
在 MaxPQ 中加入调整数组大小的代码,
并和命题 Q 一样证明对于一般性长度为 N 的队列其数组访问的上限。
官方实现中已经包含了调整数组大小的代码,见:https://algs4.cs.princeton.edu/24pq/MaxPQ.java.html
截取如下:
// helper function to double the size of the heap array private void resize(int capacity) { assert capacity > n; Key[] temp = (Key[]) new Object[capacity]; for (int i = 1; i <= n; i++) { temp[i] = pq[i]; } pq = temp; } 只要在队列快满时重新分配空间,再把元素复制进去即可。
在不触发重新分配空间的情况下,
每次队列操作的比较次数上限就等于命题 Q 中给出的 $ \lg N+1 $(插入) 和 $ 2\lg N $(删除)。
插入元素最多需要 $ \lg N $ 次交换(比较次数-1),
删除元素最多需要 \(1 + \lg N - 1 = \lg N\) 次交换 (注意开始时有一次交换)。
同时一次比较需要 $ 2 $ 次数组访问,一次交换需要 \(4\) 次数组访问(记 a[i] 为一次数组访问)。
换算成数组访问次数就是 $ 6 \lg N + 2 $(插入)和 $ 8 \lg N $ (删除)。
重新分配空间(C#)
/// <summary> /// 重新调整堆的大小。 /// </summary> /// <param name="capacity">调整后的堆大小。</param> private void Resize(int capacity) { Key[] temp = new Key[capacity]; for (int i = 1; i <= this.n; i++) { temp[i] = this.pq[i]; } this.pq = temp; } 2.4.23
Multiway 的堆。
只考虑比较的成本且假设找到 t 个元素中的最大者需要 t 次比较,
在堆排序中使用 t 向堆的情况下找出使比较次数 NlogN 的系数最小的 t 值。
首先,假设使用的是一个简单通用的 sink() 方法;
其次,假设 Floyd 方法在内循环中每轮可以节省一次比较。
sink 方法会在所有的 $ t $ 个子结点中寻找最大的结点。
如果找到的结点比当前结点大,那么就进行交换。
否则视为结点已经下沉到了合适的位置,结束循环。
根据题意,在 $ t $ 个元素中找最大值需要 $ t $ 次比较。
sink 操作需要找到 $ t $ 个子结点中的最大值并与当前结点相比较。
于是 sink 操作每次最多需要 $ t + 1 $ 次比较。
建堆过程,对 2.4.20 的证明进行推广。
设 $ t $ 叉树的高度为 $ h $ ,叶子结点的高度为 $ 0 $,根结点的高度为 $ h $。
根据 sink 操作的定义,高度为 $ k $ 的结点最多进行 $ k $ 次交换(到达叶子结点)。
于是建堆需要的总交换次数为:
\[ \begin{align*} & h+t(h-1)+t^2(h-2)+ \dots + t^h(0) \\ & =\sum_{k=0}^{h-1} t^k(h-k) \\ & =h\sum_{k=0}^{h-1}t^k - \sum_{k=0}^{h-1}kt^k \\ \end {align*} \]
其中,第一个数列是等比数列,第二个数列是等差数列和等比数列之积,可以利用错位相减法求得,即:
\[ \begin{align*} & h\sum_{k=0}^{h-1}t^k - \sum_{k=0}^{h-1}kt^k \\ & =\frac{h-ht^{h}}{1-t}-\sum_{k=0}^{h-1}kt^k \\ & =\frac{h-ht^{h}}{1-t} -\frac{\sum kt^k - t\sum kt^k}{1-t} \\ & =\frac{h-ht^h}{1-t}-\frac{t(1-t^{h-1})}{(1-t)^2}+\frac{(h-1)t^h}{1-t} \\ & =\frac{h-t^h}{1-t}-\frac{t(1-t^{h-1})}{(1-t)^2} \\ & =\frac{h-ht+t^{h+1}-t}{(1-t)^2} \end{align*} \]
考虑到对于 $ t $ 叉堆,结点数可以表示为 $ n=\frac{t^{h+1}-1}{t-1} $ 。故交换次数可以化简为:
\[ \begin{align*} & \frac{h-ht+t^{h+1}-t}{(1-t)^2} \\ & =\frac{h-ht+t^{h+1}-t +1-1}{(1-t)^2} \\ & =\frac{t^{h+1}-1}{(1-t)^2}+\frac{h-ht-t+1}{(1-t)^2} \\ & =-\frac{n}{1-t}+\frac{h}{1-t}+\frac{1}{1-t} \\ & =\frac{n-h-1}{t-1} \le n \end{align*} \]
故建堆所需比较次数最大为 $ (t+1)n $。
每次删除最大元素都会对根结点调用一次 sink 操作,
因此排序所需的比较次数最多为 $ (t+1)n\log_t(n) $。
相加得堆排序所需的总交换次数最多为 $ (t+1)n + (t+1)n\log_t(n) =(t+1)(n\log_tn+n) $ 。
利用换底公式将对数的底换成 2,得到:$ \frac{t+1}{\lg t} n\log n $。
于是问题变为求 $ f(t)= \frac{t+1}{\lg t} $ 的最小值,对其求导,得到:
\[ ( \frac{t+1}{\lg t} )'=\frac{-t+t\ln t-1}{t\ln^2t}・\ln 2 \]
直接求导数的零点会比较困难,但利用勘根公式可以寻找到根所在的区间。
由于 \(\ln 2\) 不影响正负,我们直接将其去掉,变为
\[ \frac{-t+t\ln t-1}{t\ln^2t}=\frac{-1+\ln t-\frac{1}{t}}{\ln^2t} \]
由于 $ t > 1 $,分母总是为正,因此导函数正负就等于下面这个函数的正负:
\[ \begin {align*} g(t)=\ln t -1-\frac{1}{t} \end {align*} \]
$ t = e $ 时 $ g(t) < 0 $ ,$ t=e+1 $ 时 $ g(t) > 0 $。于是可以求得在 $ (e, e+1) $ 上 $ f(t) $ 存在极小值。
又由于 $ g(t) $ 在 $ (e + 1, +\infty) $ 始终为正,因此在 $ (e, e+1) $ 上存在的是最小值($ t \ge 2 $)。
因为 $ t $ 为大于 $ 1 $ 的正整数,且 $ f(4) < f(3) $,故 $ t=4 $ 时系数最小,此时系数为 $ 2.5 $。
在删除最大元素的过程中,根结点会和最后一个结点交换,然后对新的根结点执行 sink 操作。
大多数情况下,这个结点会被一路交换到树的最后一层。
因此我们省去 sink 操作中与自己比较的过程,直接和子结点中的较大者进行交换。
这样一路交换到树的底部,随后再让这个结点与自己的父结点比较,向上「回到」合适的位置。
大多数结点都不需要向上交换,
利用 Floyd 方法对于建堆没有影响(建堆也可以使用 Floyd 方法,参见「另请参阅」部分)。
于是建堆的比较次数仍为 $ (t+1)n $。
排序的比较次数变为 $ tn\log_t(n) $。
总的比较次数变为 $ (t+1)n + tn\log_t(n) $。
我们仍然只关心 \(n\lg n\) 的系数,系数为 $ f(t)= \frac{t}{\lg t} $。
按照之前的方法再求一次最小值,求得 $ t = 3 $ 时系数最小,此时系数为 $ 1.89 $。
Floyd 提出的堆排序优化
Floyd R W. Algorithm 245: treesort[J]. Communications of the ACM, 1964, 7(12): 701.
通过将这种方法应用到建堆获得的快速建堆方法
McDiarmid C J H, Reed B A. Building heaps fast[J]. Journal of algorithms, 1989, 10(3): 352-365.
2.4.24
使用链接的优先队列。
用堆排序的二叉树实现一个优先队列,但使用链表结构代替数组。
每个结点都需要三个链接:两个向下,一个向上。
你的实现即使在无法预知队列大小的情况下也能保证优先队列的基本操作所需时间为对数级别。
链式实现,每个结点都包含一个指向父结点的指针和两个指向子结点的指针。
交换结点可以直接用交换两个结点的值来实现(与数组的实现一样),而不是对两个结点的指针进行交换。
于是 Sink() 和 Swim() 操作就比较简单,直接按照定义实现即可。
比较困难的是删除和插入结点,或者更具体的说,
如何找到按照完全二叉树定义下序号向后/向前一位的结点?
我们首先在堆里面维护两个指针,一个指向根结点(root),另一个指向当前最后一个结点(last)。
当需要插入新结点时,我们需要找到 last 的后一位的父结点,然后把新的结点插入为该结点的左子结点。
这段话可能比较绕,下面这个示意图可以帮助理解,有三种情况:

标黄的代表
last 指着的位置。我们先从简单的说起,中间的第二种情况,新插入的结点应该放在右侧,即作为
last 的父结点的右子结点。如果
last 已经是右子结点了,那么就考虑第三种情况。此时应该向上回溯,直到在某一次回溯中,结点是从父结点的左侧回溯上来的
(即图中路径 A-B-B,B-B 这一步是从左子树回溯上来的)。
于是待插入的位置就在该父结点的右子树的最左侧结点(即图中根结点的右子结点 A)。
最后是图中第一种情况,整棵树已经是满二叉树了。
这种情况下会一路回溯到根结点,那么只要一路下沉到最左侧的叶子结点,把新结点插入到其左子树上即可。
删除结点同理,也是这三种情况,只是需要找前一个结点,判断条件中的左右正好相反。
如果已经是右子结点了,只需要把 last 改为其父结点的左子树即可。
如果是左子结点,就需要回溯,直到某一次回溯是从右子树回溯上来的,last 应该指向其左子树的最右侧结点。
如果删除后正好变成满二叉树,那么会一直回溯到根结点,last 应该指向整棵树的最右侧结点。
代码实现中还需要处理只有一个结点以及没有结点时的特殊情况。
根据上面的算法,插入/删除找到相应位置所需的最大耗时为 2lgN
(从树的一侧回溯到根结点,再下沉到另一侧的底部)。
Sink 和 Swim 是 O(lgN) 级的,因此整个插入/删除操作是 O(lgN) 的。
using System; namespace PriorityQueue { /// <summary> /// 基于链式结构实现的最大堆。 /// </summary> /// <typeparam name="Key">优先队列中保存的数据类型。</typeparam> public class MaxPQLinked<Key> : IMaxPQ<Key> where Key : IComparable<Key> { /// <summary> /// 二叉堆的根结点。 /// </summary> private TreeNode<Key> root = null; /// <summary> /// 二叉堆的最后一个结点。 /// </summary> private TreeNode<Key> last = null; /// <summary> /// 二叉堆中的结点个数。 /// </summary> private int nodesCount = 0; /// <summary> /// 建立一个链式结构的最大堆。 /// </summary> public MaxPQLinked() { } /// <summary> /// 删除并返回最大值。 /// </summary> /// <returns>最大值。</returns> public Key DelMax() { Key result = this.root.Value; Exch(this.root, this.last); if (this.nodesCount == 2) { this.root.Left = null; this.last = this.root; this.nodesCount--; return result; } else if (this.nodesCount == 1) { this.last = null; this.root = null; this.nodesCount--; return result; } // 获得前一个结点。 TreeNode<Key> newLast = this.last; if (newLast == this.last.Prev.Right) newLast = this.last.Prev.Left; else { // 找到上一棵子树。 while (newLast != this.root) { if (newLast != newLast.Prev.Left) break; newLast = newLast.Prev; } // 已经是满二叉树。 if (newLast == this.root) { // 一路向右,回到上一层。 while (newLast.Right != null) newLast = newLast.Right; } // 不是满二叉树。 else { // 向左子树移动,再一路向右。 newLast = newLast.Prev.Left; while (newLast.Right != null) newLast = newLast.Right; } } // 删除最后一个结点。 if (this.last.Prev.Left == this.last) this.last.Prev.Left = null; else this.last.Prev.Right = null; Sink(this.root); // 指向新的最后一个结点。 this.last = newLast; this.nodesCount--; return result; } /// <summary> /// 插入一个新的结点。 /// </summary> /// <param name="v">待插入的结点。</param> public void Insert(Key v) { TreeNode<Key> item = new TreeNode<Key>(v); // 堆为空。 if (this.last == null) { this.root = item; this.last = item; this.nodesCount++; return; } // 堆只有一个结点。 if (this.last == this.root) { item.Prev = this.root; this.root.Left = item; this.last = item; this.nodesCount++; Swim(item); return; } // 定位到最后一个节点的父结点。 TreeNode<Key> prev = this.last.Prev; // 右子节点为空,插入到右子节点。 if (prev.Right == null) { item.Prev = prev; prev.Right = item; } else { // 当前子树已满,需要向上回溯。 // 找到下一个子树(回溯的时候是从左子树回溯上去的)。 while (prev != this.root) { if (prev != prev.Prev.Right) break; prev = prev.Prev; } // 已经是满二叉树。 if (prev == this.root) { // 一路向左,进入下一层。 while (prev.Left != null) prev = prev.Left; item.Prev = prev; prev.Left = item; } // 不是满二叉树。 else { // 向右子树移动,再一路向左。 prev = prev.Prev.Right; while (prev.Left != null) prev = prev.Left; item.Prev = prev; prev.Left = item; } } this.last = item; this.nodesCount++; Swim(item); return; } /// <summary> /// 返回二叉堆是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.root == null; /// <summary> /// 返回二叉堆中的最大值。 /// </summary> /// <returns></returns> public Key Max() => this.root.Value; /// <summary> /// 返回二叉堆中的元素个数。 /// </summary> /// <returns></returns> public int Size() => this.nodesCount; /// <summary> /// 使结点上浮。 /// </summary> /// <param name="k">需要上浮的结点。</param> private void Swim(TreeNode<Key> k) { while (k.Prev != null) { if (Less(k.Prev, k)) { Exch(k.Prev, k); k = k.Prev; } else break; } } /// <summary> /// 使结点下沉。 /// </summary> /// <param name="k">需要下沉的结点。</param> private void Sink(TreeNode<Key> k) { while (k.Left != null || k.Right != null) { TreeNode<Key> toExch = null; if (k.Left != null && k.Right != null) toExch = Less(k.Left, k.Right) ? k.Right : k.Left; else if (k.Left != null) toExch = k.Left; else toExch = k.Right; if (Less(k, toExch)) Exch(k, toExch); else break; k = toExch; } } /// <summary> /// 交换二叉堆中的两个结点。 /// </summary> /// <param name="a">要交换的第一个结点。</param> /// <param name="b">要交换的第二个结点。</param> private void Exch(TreeNode<Key> a, TreeNode<Key> b) { Key temp = a.Value; a.Value = b.Value; b.Value = temp; } /// <summary> /// 比较第一个结点值的是否小于第二个。 /// </summary> /// <param name="a">判断是否较小的结点。</param> /// <param name="b">判断是否较大的结点。</param> /// <returns></returns> private bool Less(TreeNode<Key> a, TreeNode<Key> b) => a.Value.CompareTo(b.Value) < 0; } } 2.4.25
计算数论。
编写程序 CubeSum.java,在不使用额外空间的条件下,
按大小顺序打印所有 a^3+b^3 的结果,其中 a 和 b 为 0 至 N 之间所有的整数。
也就是说,不要全部计算 N^2 个和然后排序,
而是创建一个最小优先队列,初始状态为 (0^3, 0, 0),(1^3, 0, 0),(2^3, 2, 0),...,(N^3, N, 0)。
这样只要优先队列非空,删除并打印最小的元素 (i^3+j^3, i, j)。
然后如果 j<N,插入元素 (i^3+(j+1)^3, i, j+1)。
用这段程序找出 0 到 10^6 之间所有满足 a^3+b^3 = c^3+d^3 的不同整数 a, b, c, d。
官方实现:https://algs4.cs.princeton.edu/24pq/CubeSum.java.html
因此在官方实现的基础上,每次取出最小值之后和之前的最小值比较,如果相等则输出对应的组合。
关键代码如下:
CubeSum prev = new CubeSum(-1, -1); long pairCount = 0; while (!pq.IsEmpty()) { CubeSum s = pq.DelMin(); if (s.sum == prev.sum) // 如果与之前的数相等 { Console.WriteLine(s + " = " + prev.i + "^3 + " + prev.j + "^3"); pairCount++; } if (s.j < n) pq.Insert(new CubeSum(s.i, s.j + 1)); prev = s; } 当然,对于 n=10^6 来说结果会非常大,程序的运行时间需要以天为单位计算(约 14 天)。
n=10^4 时,总共可以找到 41570 对数据。(result10K.txt, 下载大小 506 KB,解压后 1.93 MB)
n=10^5 时,总共可以找到 895023 对数据。(result100K.txt,下载大小 12.7 MB,解压后 47.5 MB)
n=10^6 时,总共可以找到 16953323 对数据。(result1M.txt,下载大小 280 MB,解压后 0.98 GB)
CubeSum.cs
using System; namespace _2._4._25 { /// <summary> /// 立方和类,保存 a^3+b^3 的值。 /// </summary> class CubeSum : IComparable<CubeSum> { /// <summary> /// 立方和。 /// </summary> internal readonly long sum; /// <summary> /// 第一个数。 /// </summary> internal readonly long i; /// <summary> /// 第二个数。 /// </summary> internal readonly long j; /// <summary> /// 建立一个立方和类。 /// </summary> /// <param name="i">立方和的第一个数。</param> /// <param name="j">立方和的第二个数。</param> public CubeSum(long i, long j) { this.sum = i * i * i + j * j * j; this.i = i; this.j = j; } /// <summary> /// 比较两个立方和的大小,返回 1, 0, -1 中的一个。 /// </summary> /// <param name="other">需要与之比较的另一个数。</param> /// <returns></returns> public int CompareTo(CubeSum other) { return this.sum.CompareTo(other.sum); } /// <summary> /// 返回 "sum = i^3 + j^3" 形式的字符串。 /// </summary> /// <returns></returns> public override string ToString() { return this.sum + " = " + this.i + "^3 + " + this.j + "^3"; } } } 主程序
using System; using System.IO; using PriorityQueue; namespace _2._4._25 { /* * 2.4.25 * * 计算数论。 * 编写程序 CubeSum.java, * 在不使用额外空间的条件下, * 按大小顺序打印所有 a^3+b^3 的结果, * 其中 a 和 b 为 0 至 N 之间所有的整数。 * 也就是说,不要全部计算 N^2 个和然后排序, * 而是创建一个最小优先队列, * 初始状态为 (0^3, 0, 0),(1^3, 0, 0),(2^3, 2, 0),...,(N^3, N, 0)。 * 这样只要优先队列非空,删除并打印最小的元素 (i^3+j^3, i, j)。 * 然后如果 j<N,插入元素 (i^3+(j+1)^3, i, j+1)。 * 用这段程序找出 0 到 10^6 之间 * 所有满足 a^3+b^3 = c^3+d^3 的不同整数 a, b, c, d。 * */ class Program { static void Main(string[] args) { int n = 1000000; MinPQ<CubeSum> pq = new MinPQ<CubeSum>(); Console.WriteLine("正在初始化"); for (int i = 0; i <= n; i++) { pq.Insert(new CubeSum(i, i)); } FileStream ostream = new FileStream("./result.txt", FileMode.Create, FileAccess.Write); StreamWriter sw = new StreamWriter(ostream); Console.WriteLine("正在写入文件……"); CubeSum prev = new CubeSum(-1, -1); long pairCount = 0; while (!pq.IsEmpty()) { CubeSum s = pq.DelMin(); if (s.sum == prev.sum) { sw.WriteLine(s + " = " + prev.i + "^3 + " + prev.j + "^3"); pairCount++; } if (s.j < n) pq.Insert(new CubeSum(s.i, s.j + 1)); prev = s; } sw.WriteLine("共找到" + pairCount + "对数据"); Console.WriteLine("共找到" + pairCount + "对数据"); sw.Close(); Console.WriteLine("结果已经保存到程序所在目录下的 result.txt 文件中"); } } } Diophantine Equation-3rd Powers - Wolfram MathWorld
PriorityQueue 库
2.4.26
无需交换的堆。
因为 sink() 和 swim() 中都用到了初级函数 exch(),所以所有元素都被多加载并存储了一次。
回避这种低效的方式,用插入排序给出新的实现(请见练习 2.1.25)。
用类似于「半交换」的方法避免频繁调用 Exch() 方法。
上浮时,先单独保存待上浮的元素,随后进行比较,
如果当前 k 值对应的父结点(即 k/2 )小于待上浮的元素,令 pq[k]=pq[k/2]。
否则令当前 k 值等于待上浮的元素,终止循环。
下沉的过程类似。
修改后的 sink 和 swim 方法:
/// <summary> /// 使元素上浮。 /// </summary> /// <param name="k">需要上浮的元素。</param> private void Swim(int k) { Key key = this.pq[k]; while (k > 1 && this.pq[k / 2].CompareTo(key) < 0) { this.pq[k] = this.pq[k / 2]; k /= 2; } this.pq[k] = key; } /// <summary> /// 使元素下沉。 /// </summary> /// <param name="k">需要下沉的元素。</param> private void Sink(int k) { Key key = this.pq[k]; while (k * 2 <= this.n) { int j = 2 * k; if (Less(j, j + 1)) j++; if (this.pq[j].CompareTo(key) < 0) break; this.pq[k] = this.pq[j]; k = j; } this.pq[k] = key; } 2.4.27
找出最小元素。
在 MaxPQ 中加入一个 min() 方法。
你的实现所需的时间和空间都应该是常数。
官网有解答,只要在 MaxPQ 里面加上一个记录最小值的指针就可以了。
初始状态下这个指针为空。
每次插入新元素的时候先更新一下这个指针。
删除最后一个元素的时候把它重新置空即可。
具体实现见代码。
using System; using System.Collections; using System.Collections.Generic; using System.Diagnostics; namespace PriorityQueue { /// <summary> /// 包含最小元素引用的最大堆。(数组实现) /// </summary> /// <typeparam name="Key">最大堆中保存的元素类型。</typeparam> public class MaxPQWithMin<Key> : IMaxPQ<Key>, IEnumerable<Key> where Key : class, IComparable<Key> { private Key[] pq; // 保存元素的数组。 private int n; // 堆中的元素数量。 private Key min; // 堆中的最小元素。 /// <summary> /// 默认构造函数。 /// </summary> public MaxPQWithMin() : this(1) { } /// <summary> /// 建立指定容量的最大堆。 /// </summary> /// <param name="capacity">最大堆的容量。</param> public MaxPQWithMin(int capacity) { this.pq = new Key[capacity + 1]; this.n = 0; this.min = null; } /// <summary> /// 从已有元素建立一个最大堆。(O(n)) /// </summary> /// <param name="keys">已有元素。</param> public MaxPQWithMin(Key[] keys) { this.n = keys.Length; this.pq = new Key[keys.Length + 1]; this.min = null; if (this.n == 0) return; // 复制元素的同时更新最小值。 this.min = keys[0]; for (int i = 0; i < keys.Length; i++) { this.pq[i + 1] = keys[i]; if (this.pq[i + 1].CompareTo(this.min) < 0) this.min = this.pq[i + 1]; } for (int k = this.n / 2; k >= 1; k--) Sink(k); Debug.Assert(IsMaxHeap()); } /// <summary> /// 删除并返回最大元素。 /// </summary> /// <returns></returns> public Key DelMax() { if (IsEmpty()) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); Key max = this.pq[1]; Exch(1, this.n--); this.pq[this.n + 1] = this.pq[1]; Sink(1); this.pq[this.n + 1] = null; if ((this.n > 0) && (this.n == this.pq.Length / 4)) Resize(this.pq.Length / 2); // 如果堆变为空。 if (IsEmpty()) this.min = null; Debug.Assert(IsMaxHeap()); return max; } /// <summary> /// 向堆中插入一个元素。 /// </summary> /// <param name="v">需要插入的元素。</param> public void Insert(Key v) { if (this.n == this.pq.Length - 1) Resize(2 * this.pq.Length); // 更新最小值。 if (this.min == null) this.min = v; else if (v.CompareTo(this.min) < 0) this.min = v; this.pq[++this.n] = v; Swim(this.n); Debug.Assert(IsMaxHeap()); } /// <summary> /// 检查堆是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.n == 0; /// <summary> /// 获得堆中最大元素。 /// </summary> /// <returns></returns> public Key Max() => this.pq[1]; /// <summary> /// 获得堆中的最小元素。 /// </summary> /// <returns></returns> public Key Min() => this.min; /// <summary> /// 获得堆中元素的数量。 /// </summary> /// <returns></returns> public int Size() => this.n; /// <summary> /// 获取堆的迭代器,元素以降序排列。 /// </summary> /// <returns></returns> public IEnumerator<Key> GetEnumerator() { MaxPQWithMin<Key> copy = new MaxPQWithMin<Key>(this.n); for (int i = 1; i <= this.n; i++) copy.Insert(this.pq[i]); while (!copy.IsEmpty()) yield return copy.DelMax(); // 下次迭代的时候从这里继续执行。 } /// <summary> /// 获取堆的迭代器,元素以降序排列。 /// </summary> /// <returns></returns> IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } /// <summary> /// 使元素上浮。 /// </summary> /// <param name="k">需要上浮的元素。</param> private void Swim(int k) { while (k > 1 && Less(k / 2, k)) { Exch(k, k / 2); k /= 2; } } /// <summary> /// 使元素下沉。 /// </summary> /// <param name="k">需要下沉的元素。</param> private void Sink(int k) { while (k * 2 <= this.n) { int j = 2 * k; if (Less(j, j + 1)) j++; if (!Less(k, j)) break; Exch(k, j); k = j; } } /// <summary> /// 重新调整堆的大小。 /// </summary> /// <param name="capacity">调整后的堆大小。</param> private void Resize(int capacity) { Key[] temp = new Key[capacity]; for (int i = 1; i <= this.n; i++) { temp[i] = this.pq[i]; } this.pq = temp; } /// <summary> /// 判断堆中某个元素是否小于另一元素。 /// </summary> /// <param name="i">判断是否较小的元素。</param> /// <param name="j">判断是否较大的元素。</param> /// <returns></returns> private bool Less(int i, int j) => this.pq[i].CompareTo(this.pq[j]) < 0; /// <summary> /// 交换堆中的两个元素。 /// </summary> /// <param name="i">要交换的第一个元素下标。</param> /// <param name="j">要交换的第二个元素下标。</param> private void Exch(int i, int j) { Key swap = this.pq[i]; this.pq[i] = this.pq[j]; this.pq[j] = swap; } /// <summary> /// 检查当前二叉树是不是一个最大堆。 /// </summary> /// <returns></returns> private bool IsMaxHeap() => IsMaxHeap(1); /// <summary> /// 确定以 k 为根节点的二叉树是不是一个最大堆。 /// </summary> /// <param name="k">需要检查的二叉树根节点。</param> /// <returns></returns> private bool IsMaxHeap(int k) { if (k > this.n) return true; int left = 2 * k; int right = 2 * k + 1; if (left <= this.n && Less(k, left)) return false; if (right <= this.n && Less(k, right)) return false; return IsMaxHeap(left) && IsMaxHeap(right); } } } 2.4.28
选择过滤。
编写一个 TopM 的用例,从标准输入读入坐标 (x, y, z),
从命令行得到值 M,然后打印出距离原点的欧几里得距离最小的 M 个点。
在 N=10^8 且 M=10^4 时,预计程序的运行时间。
开始时让 N=10^5,在 M=10^4 不变的情况下令 N 不断翻倍,求出算法增长的数量级。
再根据求出的增长的数量级估计 N=10^8 时所需要的时间。
为了方便比较,需要编写一个欧几里得距离类,
构造时输入一个点的坐标,内部自动计算并保存这个点到原点的欧几里得距离。
欧几里得距离的计算公式如下:
\[ d(x,y)=\sqrt{\sum_{i=1}^{n}(x_i-y_i)^2} \]
其中,x 和 y 分别代表两个点。
在本题中,y 始终是原点,且使用三维坐标系,因此公式可以简化为:
\[ d=\sqrt {x^2+y^2+z^2} \]
同时这个类需要实现 IComparable 接口以作为最小堆的元素。
做测试时,先随机生成 N 个点,再建立一个最小堆。
随后开始计时,把开始的 m 个点插入。
剩余的 n-m 个点则是先删除最小值再插入,这样可以保证最小堆的大小不变。
最后再把堆中的所有元素输出,停止计时。
用不断倍增的的 N 值做上述测试,获得每次的耗时,进而求得算法增长的数量级。
求得的结果如下:

欧几里得距离类,EuclideanDistance3D
using System; namespace _2._4._28 { /// <summary> /// 点到原点的欧几里得距离。 /// </summary> class EuclideanDistance3D : IComparable<EuclideanDistance3D> { private readonly int x, y, z; private double distance; /// <summary> /// 计算点到原点的欧几里得距离。 /// </summary> /// <param name="x">x 轴坐标。</param> /// <param name="y">y 轴坐标。</param> /// <param name="z">z 轴坐标。</param> public EuclideanDistance3D(int x, int y, int z) { this.x = x; this.y = y; this.z = z; this.distance = Math.Sqrt(x * x + y * y + z * z); } /// <summary> /// 比较两个欧几里得距离的大小。 /// </summary> /// <param name="other">另一个欧几里得距离。</param> /// <returns></returns> public int CompareTo(EuclideanDistance3D other) { return this.distance.CompareTo(other.distance); } /// <summary> /// 以 "(x, y, z)" 形式输出点的坐标。 /// </summary> /// <returns></returns> public override string ToString() { return "(" + this.x + ", " + this.y + ", " + this.z + ")"; } } } 测试类
using System; using System.Diagnostics; using PriorityQueue; namespace _2._4._28 { /* * 2.4.28 * * 选择过滤。 * 编写一个 TopM 的用例, * 从标准输入读入坐标 (x, y, z),从命令行得到值 M, * 然后打印出距离原点的欧几里得距离最小的 M 个点。 * 在 N=10^8 且 M=10^4 时,预计程序的运行时间。 * */ class Program { static void Main(string[] args) { // m 不变的情况下算法是 O(n) 的 // 因此预计时间是 n=10^5 的运行时间乘以 10^3 倍。 int n = 100000, m = 10000; long prev = 0; for (int i = 0; i < 6; i++) { Console.Write("n= " + n + " m= " + m); long now = test(m, n); // 获取当前 m,n 值的算法运行时间 Console.Write("\t time=" + now); if (prev == 0) { prev = now; Console.WriteLine(); } else { Console.WriteLine("\tratio=" + (double)now / prev); prev = now; } n *= 2; } } /// <summary> /// 进行一次测试。 /// </summary> /// <param name="m">测试使用的 m 值。</param> /// <param name="n">测试使用的 n 值。</param> /// <returns></returns> static long test(int m, int n) { var pq = new MinPQ<EuclideanDistance3D>(m); int[] x = new int[n]; int[] y = new int[n]; int[] z = new int[n]; Random random = new Random(); for (int i = 0; i < n; i++) { x[i] = random.Next(); y[i] = random.Next(); z[i] = random.Next(); } Stopwatch sw = new Stopwatch(); sw.Start();// 开始计时 for (int i = 0; i < m; i++) { // 先插入 m 个记录 pq.Insert(new EuclideanDistance3D(x[i], y[i], z[i])); } for (int i = m; i < n; i++) { // 插入剩余 n-m 个记录 pq.DelMin(); pq.Insert(new EuclideanDistance3D(x[i], y[i], z[i])); } while (pq.IsEmpty()) pq.DelMin(); sw.Stop();// 停止计时 return sw.ElapsedMilliseconds; } } } 2.4.29
同时面向最大和最小元素的优先队列。
设计一个数据类型,支持如下操作:
插入元素、删除最大元素、删除最小元素(所需时间均为对数级别),
以及找到最大元素、找到最小元素(所需时间均为常数级别)。
提示:用两个堆。
算法思想比较简单,但在实现上会有一些复杂。
用一个最大堆和一个最小堆,每个堆中都保存了全部数组元素,且相同的元素之间有指针相连。

插入元素时需要构建两个完全相同的元素分别插入到两个堆中。
找到最小元素和找到最大元素只需要分别返回最大堆和最小堆的堆顶元素即可。
以删除最小元素为例,先对最小堆进行 DelMin() 操作,再通过指针找到对应最大堆的元素并删除。
下面介绍删除堆中任意元素的算法。
首先将待删除元素与堆中最后一个元素交换,让堆的大小减一。
随后对交换后的元素先进行 Swim 再进行 Sink,移动到正确的位置上。
下图是一个例子,当删除最大元素 14 时,最小堆中删除元素 14 需要先 Swim。

如果堆的层数更多一些,就需要先 Swim 再 Sink。
现在来考虑一下实现,我们构建一个结点类,里面存放有当前结点的值、对应数组下标和另一个结点的指针。
/// <summary> /// 最大-最小堆中的数据结点。 /// </summary> private sealed class MinMaxNode : IComparable<MinMaxNode> { /// <summary> /// 结点的值。 /// </summary> public Key Key { get; set; } /// <summary> /// 结点在当前数组中的下标。 /// </summary> public readonly int Index; /// <summary> /// 指向孪生结点的引用。 /// </summary> public MinMaxNode Pair { get; set; } /// <summary> /// 这个类不能在外部实例化。 /// </summary> private MinMaxNode(Key key, int index) { this.Key = key; this.Index = index; } /// <summary> /// 工厂方法,建立两个孪生的结点。 /// </summary> /// <param name="key">结点中的元素。</param> /// <param name="minNode">准备放到最小堆中的结点。</param> /// <param name="maxNodeB">准备放到最大堆中的结点。</param> public static void GetNodes(Key key, int index, out MinMaxNode minNode, out MinMaxNode maxNode) { minNode = new MinMaxNode(key, index); maxNode = new MinMaxNode(key, index); minNode.Pair = maxNode; maxNode.Pair = minNode; } /// <summary> /// 比较两个元素的大小。 /// </summary> /// <param name="other">需要与之比较的另一个元素。</param> /// <returns></returns> public int CompareTo(MinMaxNode other) { return this.Key.CompareTo(other.Key); } } 然后重写堆的 Exch 方法,交换结点时只交换指针和元素值,不交换数组下标。
/// <summary> /// 重写的 Exch 方法,只交换元素和指针。 /// </summary> /// <param name="i">要交换的下标。</param> /// <param name="j">要交换的下标。</param> protected override void Exch(int i, int j) { this.pq[i].Pair.Pair = this.pq[j]; this.pq[j].Pair.Pair = this.pq[i]; MinMaxNode swapNode = this.pq[i].Pair; Key swapKey = this.pq[i].Key; this.pq[i].Key = this.pq[j].Key; this.pq[i].Pair = this.pq[j].Pair; this.pq[j].Key = swapKey; this.pq[j].Pair = swapNode; } 在最大堆和最小堆的实现中编写 Remove 方法,用于移除指定下标的元素。
/// <summary> /// 删除一个结点。 /// </summary> /// <param name="k">结点下标。</param> internal void Remove(int k) { if (k == this.n) { this.pq[this.n--] = default(Key); return; } else if (this.n <= 2) { Exch(1, k); this.pq[this.n--] = default(Key); return; } Exch(k, this.n--); this.pq[this.n + 1] = default(Key); Swim(k); Sink(k); } 最大-最小堆
Double Ended Priority Queue-Wikipedia
PriorityQueue 库
2.4.30
动态中位数查找。
设计一个数据类型,支持在对数时间内插入元素,
常数时间内找到中位数并在对数时间内删除中位数。
提示:用一个面向最大元素的堆再用一个面向最小元素的堆。
单独用一个变量存放中位数,然后前半部分元素放在一个最大堆中,后半部分元素放在一个最小堆中。
如下图所示,注意 Median 和两个堆并没有直接连接,这里只是方便理解元素顺序。

只要左右两个堆含有元素之差不超过 1,那么 Median 变量中存放的就是整个数组的中位数。
如果元素差大于 1,就需要进行调整,
把 Median 变量中存放的值插入到元素较少的堆,
再从元素较多的堆中取出元素放入 Median 变量,直到元素差不大于 1。
插入元素时,根据插入元素的大小插入到某一个堆中去,再做一次调整。
删除中位数时,去掉中位数,然后从元素较多的一侧堆中取元素补位,再进行一次调整。
编写代码时要注意堆中只有一个元素的情况需要特殊处理。
面向中位数的堆(MedianPQ.cs)
using System; namespace PriorityQueue { /// <summary> /// 面向中位数的堆。 /// </summary> public class MedianPQ<Key> where Key : IComparable<Key> { /// <summary> /// 最大堆(保存前半段元素)。 /// </summary> private MaxPQ<Key> maxPQ; /// <summary> /// 最小堆(保存后半段元素)。 /// </summary> private MinPQ<Key> minPQ; /// <summary> /// 中位数。 /// </summary> private Key median; /// <summary> /// 堆的大小 /// </summary> private int n; /// <summary> /// 默认构造函数,构造一个面向中位数的堆。 /// </summary> public MedianPQ() { this.maxPQ = new MaxPQ<Key>(); this.minPQ = new MinPQ<Key>(); this.median = default(Key); this.n = 0; } /// <summary> /// 构造一个指定容量的面向中位数的堆。 /// </summary> /// <param name="capacity">初始容量。</param> public MedianPQ(int capacity) { this.maxPQ = new MaxPQ<Key>((capacity - 1) / 2); this.minPQ = new MinPQ<Key>((capacity - 1) / 2); this.n = 0; this.median = default(Key); } /// <summary> /// 根据指定数组初始化面向中位数的堆。 /// </summary> /// <param name="keys">初始数组。</param> public MedianPQ(Key[] keys) { this.minPQ = new MinPQ<Key>(); this.maxPQ = new MaxPQ<Key>(); if (keys.Length == 0) { this.n = 0; this.median = default(Key); return; } this.n = keys.Length; this.median = keys[0]; for (int i = 1; i < keys.Length; i++) { if (this.median.CompareTo(keys[i]) < 0) this.minPQ.Insert(keys[i]); else this.maxPQ.Insert(keys[i]); } UpdateMedian(); } /// <summary> /// 向面向中位数的堆中插入一个元素。 /// </summary> /// <param name="key">需要插入的元素。</param> public void Insert(Key key) { if (this.n == 0) { this.n++; this.median = key; return; } if (key.CompareTo(this.median) < 0) this.maxPQ.Insert(key); else this.minPQ.Insert(key); this.n++; UpdateMedian(); } /// <summary> /// 删除并返回中位数。 /// </summary> /// <returns></returns> public Key DelMedian() { if (IsEmpty()) throw new ArgumentOutOfRangeException("MedianPQ underflow!"); Key median = this.median; if (this.n == 1) { this.n--; this.median = default(Key); return median; } // 从较大的一侧堆中取元素作为新的中位数。 if (this.minPQ.Size() > this.maxPQ.Size()) this.median = this.minPQ.DelMin(); else this.median = this.maxPQ.DelMax(); this.n--; return median; } /// <summary> /// 获得中位数。 /// </summary> /// <returns></returns> public Key Median() => this.median; /// <summary> /// 判断堆是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.n == 0; /// <summary> /// 更新中位数的值。 /// </summary> private void UpdateMedian() { // 根据两个堆的大小调整中位数 while (this.maxPQ.Size() - this.minPQ.Size() > 1) { this.minPQ.Insert(this.median); this.median = this.maxPQ.DelMax(); } while (this.minPQ.Size() - this.maxPQ.Size() > 1) { this.maxPQ.Insert(this.median); this.median = this.minPQ.DelMin(); } } } } 2.4.31
快速插入。
用基于比较的方式实现 MinPQ 的 API,
使得插入元素需要 ~loglogN 次比较,删除最小元素需要 ~2logN 次比较。
提示:在 swim() 方法中用二分查找来寻找祖先结点。
首先可以观察到堆有这样一个性质,从根结点到某一个叶子结点的路径是有序的,满足二分查找的条件。
但是,
从叶子结点到根结点的路径可以通过不断地令 k = k / 2 得到(从下往上只有一条路径)。
但从根结点到叶子结点的路径却不能简单地通过 k = k * 2 得到(从上往下会有两条分支)。
因此只通过堆本身是无法满足二分查找对于随机访问的要求的。
为了达到 ~loglogN 次比较,我们需要对 Swim() 方法做修改,
即,先通过一个数组来保存路径,再对这个数组进行二分查找,从而获得合适的祖先结点。
路径的长度是 ~logN(完全二叉树的性质),于是二分查找的比较次数即为 ~loglogN。
删除操作原本就是 ~2logN 的,不需要修改。
注意这样的方法仅仅只是减少了比较次数,
为了保持堆的有序,即使找到了结点的合适位置也不能直接插入,
仍然需要将路径上的结点依次下移,空出位置后再插入结点,复杂度仍然是 ~logN。
由于增加了保存路径等操作(建立了大量的小数组),实际算法的运行时间是增加的。
也可以用空间换时间,由于在堆中下标为 k 的结点到根结点的路径是唯一确定的。
因此可以提前计算好路径,用一个数组保存起来(数组的数组),在 Swim 中取出对应路径进行二分查找。
当然这样是很不划算的,除非元素比较的开销非常大。
修改后的 Swim() 方法,注意输入的路径是从下往上的。
/// <summary> /// 使元素上浮。 /// </summary> /// <param name="k">需要上浮的元素。</param> private void Swim(int k) { if (k == 1) return; // 获取路径 int heapHeight = (int)(Math.Log(this.n) / Math.Log(2)); List<int> path = new List<int>(); int temp = k; while (temp >= 1) { path.Add(temp); temp /= 2; } // lo=插入结点的父结点 hi=根结点 int lo = 1, hi = path.Count - 1; while (lo <= hi) { int mid = lo + (hi - lo) / 2; if (Greater(k, path[mid])) hi = mid - 1; // 当前值比较大,应该向下走 else lo = mid + 1; // 值较小,向根结点方向走 } for (int i = 1; i < lo; i++) { Exch(path[i - 1], path[i]); } } 2.4.32
下界。
请证明,不存在一个基于比较的对 MinPQ 的 API 的实现
能够使得插入元素和删除最小元素的操作都保证只使用 ~NloglogN 次比较。
官网解答见:https://algs4.cs.princeton.edu/24pq/
如果这样的话,堆排序的只需要 ~nloglogn 次比较即可。
根据 2.3 中的证明,基于比较的排序的下界是 ~nlogn。
因此不存在这样的最小堆。
注意上题的方法不能用于下沉操作,因为我们不能预知下沉的路径。
2.4.33
索引优先队列的实现。
按照 2.4.4.6 节的描述修改算法 2.6 来实现索引优先队列 API 中的基本操作:
使用 pq[] 保存索引,添加一个数组 keys[] 来保存元素,
再添加一个数组 qp[] 来保存 pq[] 的逆序――qp[i] 的值时 i 在 pq[] 中的位置(即索引 j,pq[j]=i)。
修改算法 2.6 的代码来维护这些数据结构。
若 i 不在队列之中,则总是令 qp[i] = -1 并添加一个方法 contains() 来检测这种情况。
你需要修改辅助函数 exch() 和 less(),但不需要修改 sink() 和 swim()。
官方实现见:https://algs4.cs.princeton.edu/24pq/IndexMaxPQ.java.html
书中算法 2.6 给出的是一个最大堆的实现,但本题给出的部分解答却是最小堆的。
同时官网给出的解答是最大堆的,这里选择和官网保持一致,给出最大堆的实现。
初看起来可能会比较难理解,但其实就是以指针为元素的堆。
堆中存放的只是指向元素的指针(如果元素在数组里那就变成了下标)。
做比较的时候要先根据指针(下标)找到对应元素,再进行比较。
再来看题目中给出的要求,keys[] 数组中用于保存元素(比如 keys[0] = ‘A’;),
而 pq[] 中保存的是元素在 key[] 数组中的下标(比如 pq[1] = 0;),
而 qp[] 中保存的是某个下标在 pq[]中 的对应位置。(比如 qp[0] = 1)。
在这三个数组中,pq[]是一个堆,我们的堆操作都作用在这个数组上。keys[] 数组中的元素不随着 pq[] 中下标的移动而移动,只有当删除或添加元素时才发生变化。qp[]与pq[]中的索引一一对应,pq[]交换时也需要交换qp[]中的对应元素。
using System; using System.Collections; using System.Collections.Generic; namespace PriorityQueue { /// <summary> /// 索引优先队列。 /// </summary> /// <typeparam name="Key">优先队列中包含的元素。</typeparam> public class IndexMaxPQ<Key> : IEnumerable<int> where Key : IComparable<Key> { /// <summary> /// 优先队列中的元素。 /// </summary> private int n; /// <summary> /// 索引最大堆。 /// </summary> private int[] pq; /// <summary> /// pq 的逆索引,pq[qp[i]]=qp[pq[i]]=i /// </summary> private int[] qp; /// <summary> /// 实际元素。 /// </summary> private Key[] keys; /// <summary> /// 建立指定大小的面向索引的最大堆。 /// </summary> /// <param name="capacity"></param> public IndexMaxPQ(int capacity) { if (capacity < 0) throw new ArgumentOutOfRangeException(); this.n = 0; this.keys = new Key[capacity + 1]; this.pq = new int[capacity + 1]; this.qp = new int[capacity + 1]; for (int i = 0; i <= capacity; i++) this.qp[i] = -1; } /// <summary> /// 将与索引 <paramref name="i"/> 相关联的元素换成 <paramref name="k"/>。 /// </summary> /// <param name="i">要修改关联元素的索引。</param> /// <param name="k">用于替换的新元素。</param> public void ChangeKey(int i, Key k) { if (!Contains(i)) throw new ArgumentNullException("队列中没有该索引"); this.keys[i] = k; Swim(this.qp[i]); Sink(this.qp[i]); } /// <summary> /// 确认堆包含某个索引 <paramref name="i"/>。 /// </summary> /// <param name="i">要查询的索引。</param> /// <returns></returns> public bool Contains(int i) => this.qp[i] != -1; /// <summary> /// 删除索引 <paramref name="i"/> 对应的键值。 /// </summary> /// <param name="i">要清空的索引。</param> public void Delete(int i) { if (!Contains(i)) throw new ArgumentOutOfRangeException("index is not in the priority queue"); int index = this.qp[i]; Exch(index, this.n--); Swim(index); Sink(index); this.keys[i] = default(Key); this.qp[i] = -1; } /// <summary> /// 删除并获得最大元素所在的索引。 /// </summary> /// <returns></returns> public int DelMax() { if (this.n == 0) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); int max = this.pq[1]; Exch(1, this.n--); Sink(1); this.qp[max] = -1; this.keys[max] = default(Key); this.pq[this.n + 1] = -1; return max; } /// <summary> /// 将索引 <paramref name="i"/> 对应的键值减少为 <paramref name="key"/>。 /// </summary> /// <param name="i">要修改的索引。</param> /// <param name="key">减少后的键值。</param> public void DecreaseKey(int i, Key key) { if (!Contains(i)) throw new ArgumentOutOfRangeException("index is not in the priority queue"); if (this.keys[i].CompareTo(key) <= 0) throw new ArgumentException("Calling IncreaseKey() with given argument would not strictly increase the Key"); this.keys[i] = key; Sink(this.qp[i]); } /// <summary> /// 将索引 <paramref name="i"/> 对应的键值增加为 <paramref name="key"/>。 /// </summary> /// <param name="i">要修改的索引。</param> /// <param name="key">增加后的键值。</param> public void IncreaseKey(int i, Key key) { if (!Contains(i)) throw new ArgumentOutOfRangeException("index is not in the priority queue"); if (this.keys[i].CompareTo(key) >= 0) throw new ArgumentException("Calling IncreaseKey() with given argument would not strictly increase the Key"); this.keys[i] = key; Swim(this.qp[i]); } /// <summary> /// 将元素 <paramref name="v"/> 与索引 <paramref name="i"/> 关联。 /// </summary> /// <param name="v">待插入元素。</param> /// <param name="i">需要关联的索引。</param> public void Insert(Key v, int i) { if (Contains(i)) throw new ArgumentException("索引已存在"); this.n++; this.qp[i] = this.n; this.pq[this.n] = i; this.keys[i] = v; Swim(this.n); } /// <summary> /// 堆是否为空。 /// </summary> /// <returns></returns> public bool IsEmpty() => this.n == 0; /// <summary> /// 获得与索引 <paramref name="i"/> 关联的元素。 /// </summary> /// <param name="i">索引。</param> /// <returns></returns> public Key KeyOf(int i) { if (!Contains(i)) throw new ArgumentNullException("队列中没有该索引"); return this.keys[i]; } /// <summary> /// 返回最大元素对应的索引。 /// </summary> /// <returns></returns> public int MaxIndex() { if (this.n == 0) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); return this.pq[1]; } /// <summary> /// 获得最大元素。 /// </summary> /// <returns></returns> public Key MaxKey() { if (this.n == 0) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); return this.keys[this.pq[1]]; } /// <summary> /// 返回堆的元素数量。 /// </summary> /// <returns></returns> public int Size() => this.n; /// <summary> /// 比较第一个元素是否小于第二个元素。 /// </summary> /// <param name="i">第一个元素。</param> /// <param name="j">第二个元素。</param> /// <returns></returns> private bool Less(int i, int j) => this.keys[this.pq[i]].CompareTo(this.keys[this.pq[j]]) < 0; /// <summary> /// 交换两个元素。 /// </summary> /// <param name="i">要交换的元素下标。</param> /// <param name="j">要交换的元素下标。</param> private void Exch(int i, int j) { int swap = this.pq[i]; this.pq[i] = this.pq[j]; this.pq[j] = swap; this.qp[this.pq[i]] = i; this.qp[this.pq[j]] = j; } /// <summary> /// 使下标为 <paramref name="k"/> 的元素上浮。 /// </summary> /// <param name="k">上浮元素下标。</param> private void Swim(int k) { while (k > 1 && Less(k / 2, k)) { Exch(k / 2, k); k /= 2; } } /// <summary> /// 使下标为 <paramref name="k"/> 元素下沉。 /// </summary> /// <param name="k">需要下沉的元素。</param> private void Sink(int k) { while (k * 2 <= this.n) { int j = 2 * k; if (j < this.n && Less(j, j + 1)) j++; if (!Less(k, j)) break; Exch(k, j); k = j; } } /// <summary> /// 获取迭代器。 /// </summary> /// <returns></returns> public IEnumerator<int> GetEnumerator() { IndexMaxPQ<Key> copy = new IndexMaxPQ<Key>(this.n); for (int i = 0; i < this.n; i++) copy.Insert(this.keys[this.pq[i]], this.pq[i]); while (!copy.IsEmpty()) yield return copy.DelMax(); } /// <summary> /// 获取迭代器。 /// </summary> /// <returns></returns> IEnumerator IEnumerable.GetEnumerator() => GetEnumerator(); } } 2.4.34
索引优先队列的实现(附加操作)。
向练习 2.4.33 的实现中添加 minIndex()、change() 和 delete() 方法。
这里给出最大堆的实现,原因同 2.4.33。
maxIndex():pq[1] 就是最小元素的下标。change():首先修改 keys 数组中对应的元素,然后对堆中该下标进行重排序。delete():先从堆中删除元素,再把 keys 和 qp 数组中的对应元素初始化。
/// <summary> /// 返回最大元素对应的索引。 /// </summary> /// <returns></returns> public int MaxIndex() { if (this.n == 0) throw new ArgumentOutOfRangeException("Priority Queue Underflow"); return this.pq[1]; } /// <summary> /// 将与索引 <paramref name="i"/> 相关联的元素换成 <paramref name="k"/>。 /// </summary> /// <param name="i">要修改关联元素的索引。</param> /// <param name="k">用于替换的新元素。</param> public void ChangeKey(int i, Key k) { if (!Contains(i)) throw new ArgumentNullException("队列中没有该索引"); this.keys[i] = k; Swim(this.qp[i]); Sink(this.qp[i]); } /// <summary> /// 删除索引 <paramref name="i"/> 对应的键值。 /// </summary> /// <param name="i">要清空的索引。</param> public void Delete(int i) { if (!Contains(i)) throw new ArgumentOutOfRangeException("index is not in the priority queue"); int index = this.qp[i]; Exch(index, this.n--); Swim(index); Sink(index); this.keys[i] = default(Key); this.qp[i] = -1; } 2.4.35
离散概率分布的取样。
编写一个 Sample 类,其构造函数接受一个 double 类型的数组 p[] 作为参数并支持以下操作:
random()――返回任意索引 i 及其概率 p[i]/T(T 是 p[] 中所有元素之和);
change(i, v)――将 p[i] 的值修改为 v。
提示:使用完全二叉树,每个结点对应一个权重 p[i]。
在每个结点记录其下子树的权重之和。
为了产生一个随机的索引,取 0 到 T 之间的一个随机数并根据各个结点的权重之和来判断沿着哪条子树搜索下去。
在更新 p[i] 时,同时更新从根节点到 i 的路径上的所有结点。
不要像堆的实现那样显式的使用指针。
本题有两个翻译错误。random() ――返回索引 i 的概率是 p[i]/T,而非返回概率和索引。(return an index i with probability p[i]/T)
最后一句指的是像堆那样使用数组而非显式指针实现二叉树。(Avoid explicit pointers, as we do for heaps.)
提示已经给出了实现方案,我们用一个例子来简单说明一下。
现在给出一个分布 p,总和 T=1,如下图所示:

为了实现这样的随机分布,我们在 0~T 之间随机一个小数,然后根据结果返回不同的值。

现在我们将这个思想应用到完全二叉树上。
每次随机的过程其实构成了一棵选择树,我们把数组 p 当作一棵树,如下图:

为方便起见,我们重新排列一下之前的随机表:

每个值的概率并没有改变,只是每个值对应的区段换了一下。
经过这样的变换后,你会发现,如果从根结点的角度看:
如果随机的值小于 0.1,对应的编号就是 1。
如果随机的值大于 0.5,那么对应编号只能是 3 或 6,即根结点的右子树。
其他情况对应编号在左子树上。
扩展到一般情况,就变成了:
如果随机数小于当前结点,直接返回当前结点的编号。
如果随机数大于左子树权值总和+当前结点的权值,减去它们,移动到右子树。
其他情况减去当前结点的权值并移动到左子树。
思想理解之后,代码实现就比较容易了,做了 100000 次实验的结果如下:

using System; namespace _2._4._35 { /// <summary> /// 离散分布的取样。 /// </summary> class Sample { public double[] P; public double[] SumP; private double T = 0; private Random random = new Random(); /// <summary> /// 构造一个离散取样类。 /// </summary> /// <param name="data">取样数据。</param> public Sample(double[] data) { // 复制权重 this.P = new double[data.Length + 1]; for (int i = 1; i <= data.Length; i++) { this.P[i] = data[i - 1]; this.T += data[i - 1]; } // 记录子树权重之和 this.SumP = new double[data.Length + 1]; for (int i = data.Length; i / 2 > 0; i--) { this.SumP[i / 2] += this.P[i]; } } /// <summary> /// 根据构造时给定的取样概率返回索引。 /// </summary> /// <returns></returns> public int Random() { double parcentage = this.random.NextDouble() * this.T; int index = 1; while (index * 2 <= this.P.Length) { // 找到结点 if (parcentage <= this.P[index]) break; // 减去当前结点,向子结点搜寻 parcentage -= this.P[index]; index *= 2; // 在左子树范围内 if (parcentage <= this.SumP[index] + this.P[index]) continue; // 在右子树范围内,减去左子树 parcentage -= this.SumP[index] + this.P[index]; index++; } return index - 1; } /// <summary> /// 修改索引 <paramref name="i"/> 的权重为 <paramref name="v"/>。 /// </summary> /// <param name="i">需要修改的索引。</param> /// <param name="v">新的权重。</param> public void Change(int i, double v) { i++; this.P[i] = v; // 重新计算总和 while (i > 0) { i /= 2; this.SumP[i] = this.P[i * 2] + this.SumP[i * 2]; if (i * 2 + 1 < this.P.Length) this.SumP[i] += this.P[i * 2 + 1] + this.SumP[i * 2 + 1]; } } } } 2.4.36
性能测试Ⅰ。
编写一个性能测试用例,用插入元素操作填满一个优先队列,
然后用删除最大元素操作删去一半元素,再用插入元素操作填满优先队列,
再用删除最大元素操作删去所有元素。
用一列随机的长短不同的元素多次重复以上过程,
测量每次运行的用时,打印平均用时或是将其绘制成图表。
测试结果如下:

可以看出增长数量级约为 O(nlogn)。
using System; using System.Diagnostics; using PriorityQueue; namespace _2._4._36 { class Program { static Random random = new Random(); static void Main(string[] args) { int doubleTime = 5; int repeatTime = 5; int n = 100000; for (int i = 0; i < doubleTime; i++) { long totalTime = 0; Console.WriteLine("n=" + n); for (int j = 0; j < repeatTime; j++) { MaxPQ<int> pq = new MaxPQ<int>(n); long time = Test(pq, n); Console.Write(time + "\t"); totalTime += time; } Console.WriteLine("平均用时:" + totalTime / repeatTime + "毫秒"); n *= 2; } } static long Test(MaxPQ<int> pq, int n) { // 生成数据 int[] initData = new int[n]; int[] appendData = new int[n / 2]; for (int i = 0; i < n; i++) initData[i] = random.Next(); for (int i = 0; i < n / 2; i++) appendData[i] = random.Next(); // 开始测试 Stopwatch stopwatch = new Stopwatch(); stopwatch.Start(); // 插入 n 个元素 for (int i = 0; i < n; i++) pq.Insert(initData[i]); // 删去一半 for (int i = 0; i < n / 2; i++) pq.DelMax(); // 插入一半 for (int i = 0; i < n / 2; i++) pq.Insert(appendData[i]); // 删除全部 for (int i = 0; i < n; i++) pq.DelMax(); stopwatch.Stop(); return stopwatch.ElapsedMilliseconds; } } } 2.4.37
性能测试Ⅱ。
编写一个性能测试用例,用插入元素操作填满一个优先队列,
然后在一秒钟之内尽可能多地连续反复调用删除最大元素和插入元素的操作。
用一列随机的长短不同的元素多次重复以上过程,
将程序能够完成的删除最大元素操作的平均次数打印出来或是绘成图表。
建立一个全局变量 isRunning ,每次 DelMax() 之前都先确认这个值是否为 true,
设立一个 Timer 在 1 秒钟之后自动将 isRunning 置为 false。
测试结果如下:

随着 n 增大,一秒钟之内能执行的 DelMax() 次数会下降。
using System; using System.Timers; using PriorityQueue; namespace _2._4._37 { class Program { static bool isRunning = true; static Random random = new Random(); static void Main(string[] args) { int doubleTime = 6; int repeatTime = 6; int n = 1000000; for (int i = 0; i < doubleTime; i++) { int totalDelCount = 0; Console.WriteLine("n=" + n); for (int j = 0; j < repeatTime; j++) { MaxPQ<int> pq = new MaxPQ<int>(n); int delCount = Test(n, pq); totalDelCount += delCount; Console.Write(delCount + "\t"); } Console.WriteLine("平均最大删除次数:" + totalDelCount / repeatTime); n *= 2; } } static int Test(int n, MaxPQ<int> pq) { Timer timer = new Timer(1000); timer.Elapsed += new ElapsedEventHandler(StopRunning); for (int i = 0; i < n; i++) { pq.Insert(random.Next()); } int delCount = 0; StartRunning(); timer.Start(); while (isRunning && !pq.IsEmpty()) { pq.DelMax(); delCount++; } timer.Stop(); return delCount; } static void StartRunning() => isRunning = true; static void StopRunning(object source, ElapsedEventArgs e) => isRunning = false; } } 2.4.38
练习测试。
编写一个练习用例,用算法 2.6 中实现的优先队列的接口方法处理实际应用中可能出现的高难度或是极端情况。
例如,元素已经有序、元素全部逆序、元素全部相同或是所有元素只有两个值。
直接构造相应的数组测试即可。
测试结果如下:

最大堆来说顺序时会比较慢,因为每次插入都要一路上升到顶部。
逆序的时候则是删除比较慢,最后一个元素是最小的元素,交换后需要一路下沉到底部。
由于元素相同的时候我们选择不交换(less(i, j) 返回 false),较多的重复元素并不会影响性能。
using System; using System.Linq; using System.Diagnostics; using PriorityQueue; namespace _2._4._38 { class Program { static Random random = new Random(); static void Main(string[] args) { int n = 200000; int repeatTimes = 5; int doubleTimes = 4; for (int i = 0; i < doubleTimes; i++) { Console.WriteLine("n=" + n); // 升序数组 long totalTime = 0; Console.Write("Ascending:\t"); for (int j = 0; j < repeatTimes; j++) { MaxPQ<int> pq = new MaxPQ<int>(n); int[] data = GetAscending(n); long time = Test(pq, data); Console.Write(time + "\t"); totalTime += time; } Console.WriteLine("Average:" + totalTime / repeatTimes); // 降序数组 totalTime = 0; Console.Write("Descending:\t"); for (int j = 0; j < repeatTimes; j++) { MaxPQ<int> pq = new MaxPQ<int>(n); int[] data = GetDescending(n); long time = Test(pq, data); Console.Write(time + "\t"); totalTime += time; } Console.WriteLine("Average:" + totalTime / repeatTimes); // 全部元素相同 totalTime = 0; Console.Write("All Same:\t"); for (int j = 0; j < repeatTimes; j++) { MaxPQ<int> pq = new MaxPQ<int>(n); int[] data = GetSame(n, 17763); long time = Test(pq, data); Console.Write(time + "\t"); totalTime += time; } Console.WriteLine("Average:" + totalTime / repeatTimes); // 只有两个值 totalTime = 0; Console.Write("Binary Dist.:\t"); for (int j = 0; j < repeatTimes; j++) { MaxPQ<int> pq = new MaxPQ<int>(n); int[] data = GetBinary(n, 15254, 17763); long time = Test(pq, data); Console.Write(time + "\t"); totalTime += time; } Console.WriteLine("Average:" + totalTime / repeatTimes); n *= 2; } } static long Test(MaxPQ<int> pq, int[] data) { Stopwatch sw = new Stopwatch(); sw.Start(); for (int i = 0; i < data.Length; i++) { pq.Insert(data[i]); } for (int i = 0; i < data.Length; i++) { pq.DelMax(); } sw.Stop(); return sw.ElapsedMilliseconds; } static int[] GetAscending(int n) { int[] ascending = new int[n]; for (int i = 0; i < n; i++) ascending[i] = random.Next(); Array.Sort(ascending); return ascending; } static int[] GetDescending(int n) { int[] descending = GetAscending(n); descending = descending.Reverse().ToArray(); return descending; } static int[] GetSame(int n, int v) { int[] same = new int[n]; for (int i = 0; i < n; i++) { same[i] = v; } return same; } static int[] GetBinary(int n, int a, int b) { int[] binary = new int[n]; for (int i = 0; i < n; i++) { binary[i] = random.NextDouble() > 0.5 ? a : b; } return binary; } } } 2.4.39
构造函数的代价。
对于 N=10^3、10^6 和 10^9,根据经验判断堆排序时构造堆所占总耗时的比例。
结果如下,约占总耗时的 2~5%。

using System; using System.Diagnostics; namespace _2._4._39 { /* * 2.4.39 * * 构造函数的代价。 * 对于 N=10^3、10^6 和 10^9, * 根据经验判断堆排序时构造堆所占总耗时的比例。 * */ class Program { static Random random = new Random(); static void Main(string[] args) { Console.WriteLine("n\tBuild\tSort\tRatio"); int n = 1000; // 当数据量到达 10^9 时会需要 2G 左右的内存 int multiTen = 7; for (int i = 0; i < multiTen; i++) { short[] data = GetRandomArray(n); Stopwatch fullSort = new Stopwatch(); Stopwatch buildHeap = new Stopwatch(); fullSort.Restart(); buildHeap.Restart(); BuildHeap(data); buildHeap.Stop(); HeapSort(data); fullSort.Stop(); long buildTime = buildHeap.ElapsedMilliseconds; long fullTime = fullSort.ElapsedMilliseconds; Console.WriteLine(n + "\t" + buildTime + "\t" + fullTime + "\t" + (double)buildTime / fullTime); n *= 10; } } static short[] GetRandomArray(int n) { short[] data = new short[n]; for (int i = 0; i < n; i++) { data[i] = (short)random.Next(); } return data; } /// <summary> /// 将数组构造成堆。 /// </summary> /// <param name="data">数组。</param> static void BuildHeap(short[] data) { int n = data.Length; for (int k = n / 2; k >= 1; k--) { Sink(data, k, n); } } /// <summary> /// 利用已经生成的堆排序。 /// </summary> /// <param name="heap">最大堆。</param> static void HeapSort(short[] heap) { int n = heap.Length; while (n > 1) { Exch(heap, 1, n--); Sink(heap, 1, n); } } /// <summary> /// 令堆中的元素下沉。 /// </summary> /// <param name="pq">需要执行操作的堆。</param> /// <param name="k">需要执行下沉的结点下标。</param> /// <param name="n">堆中元素的数目。</param> static void Sink(short[] pq, int k, int n) { while (2 * k <= n) { int j = 2 * k; if (j < n && Less(pq, j, j + 1)) j++; if (!Less(pq, k, j)) break; Exch(pq, k, j); k = j; } } /// <summary> /// 比较堆中下标为 <paramref name="a"/> 的元素是否小于下标为 <paramref name="b"/> 的元素。 /// </summary> /// <param name="pq">元素所在的数组。</param> /// <param name="a">需要比较是否较小的结点序号。</param> /// <param name="b">需要比较是否较大的结点序号。</param> /// <returns></returns> static bool Less(short[] pq, int a, int b) => pq[a - 1].CompareTo(pq[b - 1]) < 0; /// <summary> /// 交换堆中的两个元素。 /// </summary> /// <param name="pq">要交换的元素所在堆。</param> /// <param name="a">要交换的结点序号。</param> /// <param name="b">要交换的结点序号。</param> static void Exch(short[] pq, int a, int b) { short temp = pq[a - 1]; pq[a - 1] = pq[b - 1]; pq[b - 1] = temp; } } } 2.4.40
Floyd 方法。
根据正文中 Floyd 的先沉后浮思想实现堆排序。
对于 N=10^3、10^6 和 10^9 大小的随机不重复数组,
记录你的程序所使用的比较次数和标准实现所使用的比较次数。
如同书上所说,可以节省约 50% 的比较次数。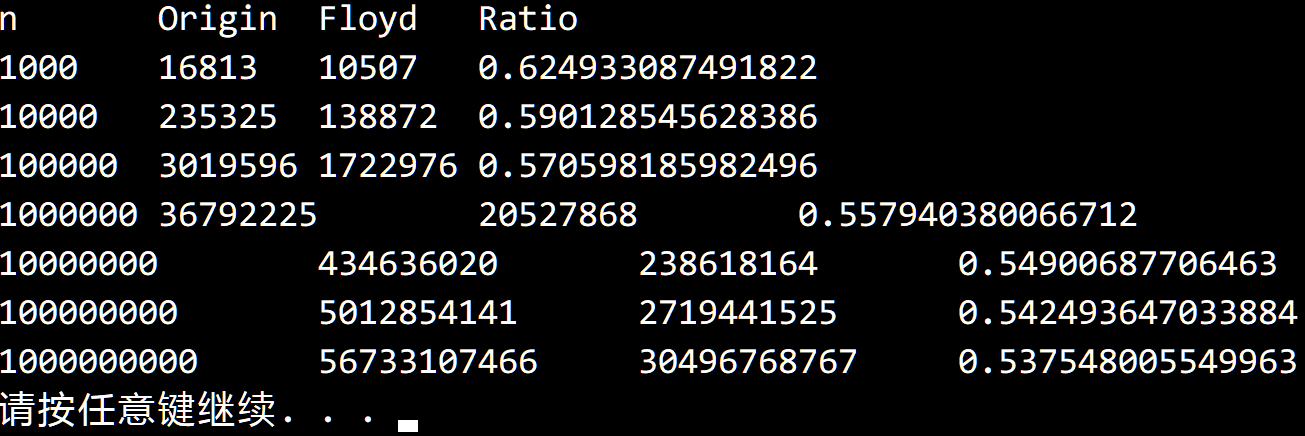
先沉后浮的实现也很简单,将 swim 方法加入,
然后修改 sink 方法,去掉其中检查是否需要下沉的条件(if(!Less(pq, k, j))),
然后在 sink 方法的循环之后调用 swim。
为了获得比较次数,你可以添加一个静态全局变量 compareCount,
然后修改 Less 方法,在作比较的同时使 compareCount++ ,
每次执行 Sort 时先让 compareCount 置零,最后返回 compareCount。
using System; namespace PriorityQueue { /// <summary> /// 堆排序类,提供 Floyd 优化的堆排序的静态方法。 /// </summary> /// <typeparam name="T">需要排序的元素类型。</typeparam> public static class HeapFloyd { /// <summary> /// 利用堆排序对数组进行排序。 /// </summary> /// <param name="pq">需要排序的数组。</param> public static void Sort<T>(T[] pq) where T : IComparable<T> { int n = pq.Length; // 建堆 for (int k = n / 2; k >= 1; k--) { Sink(pq, k, n); } // 排序 while (n > 1) { Exch(pq, 1, n--); SinkThenSwim(pq, 1, n); } } /// <summary> /// 令堆中的元素下沉。 /// </summary> /// <param name="pq">需要执行操作的堆。</param> /// <param name="k">需要执行下沉的结点下标。</param> /// <param name="n">堆中元素的数目。</param> private static void Sink<T>(T[] pq, int k, int n) where T : IComparable<T> { while (2 * k <= n) { int j = 2 * k; if (j < n && Less(pq, j, j + 1)) j++; if (!Less(pq, k, j)) break; Exch(pq, k, j); k = j; } } /// <summary> /// 先下沉后上浮。 /// </summary> /// <typeparam name="T">堆中的元素类型。</typeparam> /// <param name="pq">包含堆元素的数组。</param> /// <param name="k">要下沉的元素。</param> /// <param name="n">元素数量。</param> private static void SinkThenSwim<T>(T[] pq, int k, int n) where T : IComparable<T> { while (2 * k <= n) { int j = 2 * k; if (j < n && Less(pq, j, j + 1)) j++; Exch(pq, k, j); k = j; } Swim(pq, k); } /// <summary> /// 使元素上浮。 /// </summary> /// <param name="k">需要上浮的元素。</param> private static void Swim<T>(T[] pq, int k) where T : IComparable<T> { while (k > 1 && Less(pq, k / 2, k)) { Exch(pq, k, k / 2); k /= 2; } } /// <summary> /// 比较堆中下标为 <paramref name="a"/> 的元素是否小于下标为 <paramref name="b"/> 的元素。 /// </summary> /// <param name="pq">元素所在的数组。</param> /// <param name="a">需要比较是否较小的结点序号。</param> /// <param name="b">需要比较是否较大的结点序号。</param> /// <returns></returns> private static bool Less<T>(T[] pq, int a, int b) where T : IComparable<T> => pq[a - 1].CompareTo(pq[b - 1]) < 0; /// <summary> /// 交换堆中的两个元素。 /// </summary> /// <param name="pq">要交换的元素所在堆。</param> /// <param name="a">要交换的结点序号。</param> /// <param name="b">要交换的结点序号。</param> private static void Exch<T>(T[] pq, int a, int b) { T temp = pq[a - 1]; pq[a - 1] = pq[b - 1]; pq[b - 1] = temp; } } } 2.4.41
Multiway 堆。
根据正文中的描述实现基于完全堆有序的三叉树和四叉树的堆排序。
对于 N=10^3、10^6 和 10^9 大小的随机不重复数组,
记录你的程序所使用的比较次数和标准实现所使用的比较次数。
多叉堆和二叉堆的实现上并没有很大的区别,
只不过下沉(Sink)时需要比较的子结点数量变多了,上浮时父结点的下标不再是 $ \lfloor k /2 \rfloor $。
于是只要能推出 $ d $ 叉堆的下标换算公式即可解决整个问题。
先考虑 $ d $ 叉堆的在数组中的保存方式,
第一层显然只有根结点,第二层显然有 $ d $ 个结点,第三层则有 $ d \times d=d^2 $ 个结点,如下图所示:

接下来我们对其标号,根结点为 1,以此类推,如下图:

现在我们来推导某个结点的子结点的下标公式。
结点 $ i $ 的第一个子结点在哪里呢?
首先要加上本层剩下的结点,再加上它前面结点的所有子结点,再下一个就是它的第一个子结点了。
以 2 号结点为例,它是第二层的第一个结点,第二层共有 $ d^{2-1}=d $ 个结点,剩下 $ d-1 $ 个结点。
2 号结点前面没有更多兄弟结点,于是第一个子结点下标即为 $ 2 + d - 1 + 1= 2 + d $。
3 号结点之后剩余 $ d-2 $ 个结点,加上前面 2 号结点的 $ d $ 个子结点,
它的第一个子结点下标为 $ 3+d-2+d+1= 2+2d $。
不难发现规律,结点序号加一,子结点的下标就要对应加上 $ d \((要加上前一个结点的子结点), 这个规律也可以从图上(\) d=3 $)看出来:

1号结点的子结点范围是 $ [2,d+1] $,每加一个结点子结点就要加上 $ d $ 。
于是立即可以推得结点 $ i $ 的子结点下标范围是 $ [d(i-1)+2,di+1] $ 。
代入 $ d=2 $,可以发现是符合我们已知的规律的。
接下来是结点 $ i $ 的父结点,
我们由上面的式子反推可以得到父结点的下标为 $ \lfloor (i-2)/d \rfloor +1$(或者 \(\lceil (i-2)/d \rceil\))。
获得这两个公式之后,只需要将 sink 和 swim 方法中上升和下降的公式做相应更改即可。
测试结果,注意下标可能会超过 int 的范围,请使用 long。:

using System; namespace PriorityQueue { /// <summary> /// d 叉堆排序类,提供堆排序的静态方法。 /// </summary> /// <typeparam name="T">需要排序的元素类型。</typeparam> public static class HeapMultiway { /// <summary> /// 利用堆排序对数组进行排序。 /// </summary> /// <param name="pq">需要排序的数组。</param> /// <param name="d">堆的分叉数。</param> public static void Sort<T>(T[] pq, int d) where T : IComparable<T> { int n = pq.Length; // 建堆 for (int k = (n - 2) / d + 1; k >= 1; k--) { Sink(pq, k, n, d); } // 排序 while (n > 1) { Exch(pq, 1, n--); Sink(pq, 1, n, d); } } /// <summary> /// 令堆中的元素下沉。 /// </summary> /// <param name="pq">需要执行操作的堆。</param> /// <param name="k">需要执行下沉的结点下标。</param> /// <param name="n">堆中元素的数目。</param> /// <param name="d">堆的分叉数。</param> private static void Sink<T>(T[] pq, int k, int n, int d) where T : IComparable<T> { while ((k - 1) * d + 2 <= n) { int j = d * (k - 1) + 2; // 在 d 个子结点中找到最大的那个 for (int i = 0, q = j; i < d; i++) { if (q + i <= n && Less(pq, j, q + i)) j = q + i; } if (!Less(pq, k, j)) break; Exch(pq, k, j); k = j; } } /// <summary> /// 比较堆中下标为 <paramref name="a"/> 的元素是否小于下标为 <paramref name="b"/> 的元素。 /// </summary> /// <param name="pq">元素所在的数组。</param> /// <param name="a">需要比较是否较小的结点序号。</param> /// <param name="b">需要比较是否较大的结点序号。</param> /// <returns></returns> private static bool Less<T>(T[] pq, int a, int b) where T : IComparable<T> => pq[a - 1].CompareTo(pq[b - 1]) < 0; /// <summary> /// 交换堆中的两个元素。 /// </summary> /// <param name="pq">要交换的元素所在堆。</param> /// <param name="a">要交换的结点序号。</param> /// <param name="b">要交换的结点序号。</param> private static void Exch<T>(T[] pq, int a, int b) { T temp = pq[a - 1]; pq[a - 1] = pq[b - 1]; pq[b - 1] = temp; } } } D-ary Heap-Wikipedia
PriorityQueue 库
2.4.42
堆的前序表示。
用前序法而非级别表示一棵堆有序的树,并基于此实现堆排序。
对于 N=10^3、10^6 和 10^9 大小的随机不重复数组,
记录你的程序所使用的比较次数和标准实现所使用的比较次数。
二叉树前序遍历的顺序是:自身,左子树,右子树。
因此对于一个前序遍历序列,第一个元素是根结点,第二个元素是左子结点。
再把左子结点找到,就可以把数组分成三部分:根结点,左子树,右子树,进而递归的构造出整个二叉树。
现在问题是,右子结点在哪,或者说,左子树有多大?
这里就要用到完全二叉树的性质了,我们先从比较简单的满二叉树入手。
就满二叉树而言,根结点的左子树和右子树是一样大的,即左右子树大小均为 $ (n-1)/2 $ 。
在这种情形下,右子结点的下标显然是 $ (n+1)/2 $ ,根结点下标为 0。

完全二叉树可以视为在满二叉树的基础上加了一层叶子结点,现在我们已知结点总数 $ n $。
于是可以求得二叉树的高度 $ k=\lfloor \log_2(n) \rfloor $ ,注意只有一个结点的树高度为 0。
那么最后一层的叶子结点数目为 $ l=n-2^{k}+1 $ 个,如下图所示:

如果把最后一层(第 $ k $ 层)去掉,剩余部分即为高度为 $ k-1 $ 的满二叉树,结点总数为 $ 2^k - 1 $ 。
按照之前的说明可以知道左右子树大小都等于 $ (2^{k}-2)/2=2^{k-1}-1 $。
现在要将第 $ k $ 层的 $ l $ 个结点分到左右子树里面去。
第 $ k $ 层最多能有 $ 2^k $ 个结点,取半就是 $ 2^k / 2 = 2^{k-1} $ 个。
于是当 $ l<=2^{k-1} $ 时,左右子树大小分别为 $ 2^{k-1}-1+l $ 和 $ 2^{k-1}-1 $ 。
当 $ l > 2^{k-1} $ 时,左右子树大小分别为 $ 2^{k} - 1 $ 和 $ 2^{k-1} -1 +l -2^{k-1}=l-1 $ 。
实际上,我们只要先取根结点,然后再取 $ 2^{k-1} -1 $ 个结点给左子树,再做判断:
如果 $ n-2^{k-1} < 2^{k}-1 $ ,那么对应第一种情况,末尾的 $ 2^{k-1}-1 $ 个结点即为右子树。
否则就是第二种情况,前面的 $ 2^k $ 个结点就是根结点和左子树,剩下的为右子树。
现在我们能够根据结点总数 $ n $ 来确定相应的完全二叉树,接下来则是如何进行堆排序。
堆排序的第一步就是建堆,建堆时最主要的就是 sink 操作了。
但前序序列中除了第一个结点(根结点)之外,其他结点的左右子结点下标是不能直接通过计算得到的。
因此在前序实现中,sink 操作只能对根结点进行,引出了下面的递归建堆方法。
如果根结点的左右两棵子树都已经是堆了,那么只要对根结点进行 sink 操作即可使整个二叉树变成堆。
第一步先检查子树的大小,如果小于等于 1 则说明是叶结点,直接返回。
否则计算出左右子结点的位置,递归地建堆。
最后对根结点进行 sink 操作。
那么这个 sink 操作是怎么做的呢?
计算得到了左右子结点的下标后,比较得出较大的那个,如果大于根结点则交换,否则返回。
交换后根结点变成了某一侧子树的根结点,递归地进行 sink 即可。
接下来是排序,最主要的操作是 DelMax。
前序序列的根结点好找,但是最后一个结点就比较麻烦了,它既可能在左子树也可能在右子树。
但我们可以根据之前的大小关系来寻找,
如果左子树小于等于 $ 2^k - 1 $ ,那么最后一个结点一定在左子树,否则就在右子树。
递归进行上述过程,直到到达叶子结点,该叶子结点就是最后一个结点。
之后我们将最后一个结点暂存,整个数组从后向前补缺(这一步将导致算法变成 $ O(n^2) $ ),
再把第一个结点放到最后的空位上,最后把存起来的结点放到第一位,对该结点进行 sink 操作。
依次往复即可完成排序。
测试结果:
这个算法在设计上与一般实现的比较次数大体相等,
只是移动数组耗时较长,这里只给到 \(10^7\)。

using System; namespace PriorityQueue { /// <summary> /// 前序堆排序类,提供堆排序的静态方法。 /// </summary> /// <typeparam name="T">需要排序的元素类型。</typeparam> public static class HeapPreorderAnalysis { private static long compareTimes = 0; /// <summary> /// 利用堆排序对数组进行排序。 /// </summary> /// <param name="pq">需要排序的数组。</param> public static long Sort<T>(T[] pq) where T : IComparable<T> { compareTimes = 0; int n = pq.Length; BuildTree(pq, 0, pq.Length); // 排序 while (n > 1) { int tail = GetTail(pq, 0, n); T temp = pq[tail]; for (int i = tail + 1; i < n; i++) pq[i - 1] = pq[i]; n--; Exch(pq, 0, n); pq[0] = temp; Sink(pq, 0, n); } return compareTimes; } private static int GetTail<T>(T[] pq, int p, int n) { if (n <= 1) return p; int k = (int)(Math.Log10(n) / Math.Log10(2)); // 高度 int left = (int)Math.Pow(2, k - 1) - 1; int right = left; if (n - left <= (int)Math.Pow(2, k)) { // 叶子结点全在左侧 left = n - right - 1; return GetTail(pq, p + 1, left); } else { left = (int)Math.Pow(2, k) - 1; right = n - left - 1; return GetTail(pq, p + 1 + left, right); } } /// <summary> /// 递归建堆。 /// </summary> /// <typeparam name="T">堆中元素。</typeparam> /// <param name="pq">堆所在的数组。</param> /// <param name="p">堆的起始下标。</param> /// <param name="n">堆的元素数目。</param> private static void BuildTree<T>(T[] pq, int p, int n) where T : IComparable<T> { if (n <= 1) return; int k = (int)(Math.Log10(n) / Math.Log10(2)); // 高度 int left = (int)Math.Pow(2, k - 1) - 1; int right = left; if (n - left <= (int)Math.Pow(2, k)) { // 叶子结点全在左侧 left = n - right - 1; } else { left = (int)Math.Pow(2, k) - 1; right = n - left - 1; } BuildTree(pq, p + 1, left); BuildTree(pq, p + 1 + left, right); Sink(pq, p, n); } /// <summary> /// 令堆中的元素下沉。 /// </summary> /// <param name="pq">需要执行操作的堆。</param> /// <param name="p">需要执行下沉的结点下标。</param> /// <param name="n">堆中元素的数目。</param> private static void Sink<T>(T[] pq, int p, int n) where T : IComparable<T> { if (n <= 1) return; int k = (int)(Math.Log10(n) / Math.Log10(2)); // 高度 int left = (int)Math.Pow(2, k - 1) - 1; int right = left; if (n - left <= (int)Math.Pow(2, k)) { // 叶子结点全在左侧 left = n - right - 1; } else { left = (int)Math.Pow(2, k) - 1; right = n - left - 1; } // 找出较大的子结点 int j = p + 1, size = left; if (right != 0) // 有右结点 { if (Less(pq, j, p + left + 1)) { j = p + left + 1; size = right; } } // 与根结点比较 if (!Less(pq, p, j)) return; // 交换,继续下沉 Exch(pq, p, j); Sink(pq, j, size); } /// <summary> /// 比较堆中下标为 <paramref name="a"/> 的元素是否小于下标为 <paramref name="b"/> 的元素。 /// </summary> /// <param name="pq">元素所在的数组。</param> /// <param name="a">需要比较是否较小的结点序号。</param> /// <param name="b">需要比较是否较大的结点序号。</param> /// <returns></returns> private static bool Less<T>(T[] pq, int a, int b) where T : IComparable<T> { compareTimes++; return pq[a].CompareTo(pq[b]) < 0; } /// <summary> /// 交换堆中的两个元素。 /// </summary> /// <param name="pq">要交换的元素所在堆。</param> /// <param name="a">要交换的结点序号。</param> /// <param name="b">要交换的结点序号。</param> private static void Exch<T>(T[] pq, int a, int b) { T temp = pq[a]; pq[a] = pq[b]; pq[b] = temp; } } }